Séparation des variables : loi de Fick.

[Kley]

Salut,
Je dois résoudre cette équa diff à variable séparé.

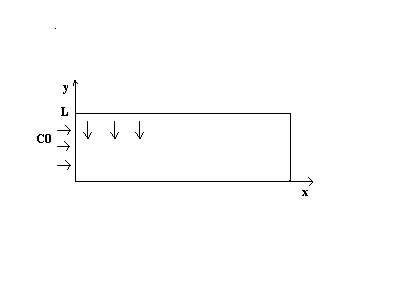
Pour info, elle représente la diffusion bidimensionnelle d’un soluté,(Premiere loi de Fick),

La méthode de résolution de cette equa diff m’a était imposée, c’est la méthode des variables séparées.

Voici mes conditions aux limites :
A y=L
A x=0

Donnez moi un coup de main, merci d’avance.

[Rincevent]

salut,

ça veut dire et ce sont des constantes ces gens-là ?

[Kley]

et ce sont des constantes ces gens-là ?

Oui, c'est exactement cela.
D : coefficient de diffusion (constant),
: vitesse (constante).

[Rincevent]

dans ce cas tu introduis des fonctions A et B telles que c(x,y)=A(x)B(y) et tu écris ton équation sous la forme f(A,A',A'',x)=g(B,B',y)=K où les ' désignent des dérivées par rapport à la seule variable dont dépend la fonction et où K sera une "vraie constante".

cf l'exemple II de la partie PDE du wiki anglophone

[Kley]

oula ça me parait pas évident,faut dire que je n'ai jamais manipuler cette méthode de séparation des variables; en plus ds l’exemple il traite une equa du type:
et non pas :


Bon j’espère que les forumeurs me viendront en aide par de plus amples détails.

Ciao.

[deep_turtle]

Bonjour,

j’espère que les forumeurs me viendront en aide par de plus amples détails.

C'est-à-dire ? Je vois pas en quoi c'est compliqué : tu cherches une fonction de la forme f(x)g(y), tu reportes cette forme dans l'équation de départ et tu t'aperçois que tu peux mettre tous les termes dépendant de x à gauche et ceux dépendant de y à droite. À quelle étape bloques-tu ?

[Kley]

Bonjour,
C'est-à-dire ? Je vois pas en quoi c'est compliqué : tu cherches une fonction de la forme f(x)g(y), tu reportes cette forme dans l'équation de départ et tu t'aperçois que tu peux mettre tous les termes dépendant de x à gauche et ceux dépendant de y à droite. À quelle étape bloques-tu ?

Salut,
Je bloque à plusieurs reprises, mais très bien on va procéder par étape :
Je pose =X(x) Y(y) ,on remplace dans l’équation principal et on abouti à:



Pourquoi c’est =-je suis d’accord pour dire que ça doit être une constante mais pour quel raison négative et elevée au carré ?

[deep_turtle]

La constante peut être a priori positive ou négative. Essaie avec une constante positive, et tu verras que la solution en X part aux fraises... (essaie, vraiment !).

Une fois convaincu que la constante doit être négative, ben tu l'écris comme l'opposé d'un carré, qui lui est nécessairement positif. Il se trouve que tu auras besoin un peu plus tard de la racine carrée de l'opposé de cette constante négative, alors autant prendre les devants et la noter -lambda^2. Mais rien ne t'empêche de la noter autrement, aucun problème !

[Kley]

La constante peut être a priori positive ou négative. Essaie avec une constante positive, et tu verras que la solution en X part aux fraises... (essaie, vraiment !).

Re
Si je prend ma constante = +
J’aurais X’’- X= 0 E.D.L homogène du second ordre.
J’aurais donc une solution:
X(x)=Aexp- + Bexp+ .
Par contre si je la pose= -j’aurais :
X(x)=(A cos x + B sin x)
Désolé mais je ne me rends pas compte de la difficulté lié au choix de la constante ?
Bref de l’autre coté je trouve
Y=C exp( + t).

voila, comment je poursuis...
Ps:merci pour l'aide.

[deep_turtle]

C'est quoi physiquement X et Y dans ton problème ? Si tu implémentes les conditions aux limites, la solution exponentielle tend vers l'infini quand X tend vers l'infini. Est-ce acceptable ? (peut-être que oui après tout, ça dépend de ton problème !)

Bref de l’autre coté je trouve

Heu... non, c'est pas ça la solution de ton équation en Y ! Il faut d'ailleurs te poser les mêmes questions sur l'influence du signe de la constante sur la solution en Y, c'est peut-être là que ça va coincer !

[Kley]

C'est quoi physiquement X et Y dans ton problème ? Si tu implémentes les conditions aux limites, la solution exponentielle tend vers l'infini quand X tend vers l'infini. Est-ce acceptable ? (peut-être que oui après tout, ça dépend de ton problème !)

Heu... non, c'est pas ça la solution de ton équation en Y ! Il faut d'ailleurs te poser les mêmes questions sur l'influence du signe de la constante sur la solution en Y, c'est peut-être là que ça va coincer !

tu parle de x,y non pas de Y,X?

x,y sont mes coordonnées cartesiennes.

[deep_turtle]

tu parle de x,y non pas de Y,X?

x,y sont mes coordonnées cartesiennes.

Je parle de tes coordonnées, oui (tu les as notées X et Y dans la première équation). Si ce sont des coordonnées cartésiennes représentant la position dans un plan, je repose ma question :

Si tu implémentes les conditions aux limites, la solution exponentielle tend vers l'infini quand X tend vers l'infini. Est-ce acceptable ?

[Kley]

ce n'est pas un t mais un y
Y=C exp( + y)
Voici mes conditions aux limites:
A y=L =0
A x=0 !!!

[deep_turtle]

Bin non, mets cette forme de Y dans l'équation (celle aux variables séparées), tu verras que ça marche pas... D'ailleurs, tu as défini Y comme ne dépendant que de y, tu ne peux pas avoir du x dedans !

[Kley]

tu veux dire celle la:


c'est pas plutot un probleme avec ma fonctionX(x)!!?