Je pourrais avoir un avis sur le schéma ?
-----

Je pourrais avoir un avis sur le schéma ?



Bonjour.
Une fois que le gaz a diffusé dans le liquide, la seule chose qu'il peut faire c'est de continuer à diffuser. Il va pas se mettre a revenir vers la bulle.
La couche avec du gaz ne peut que augmenter d'épaisseur toujours à cause de la diffusion.
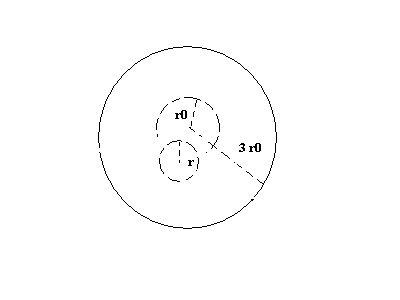
Une couche d'épaisseur 3r autour d'une bulle de rayon r me donne une sphère de rayon 4r.Bon c’est clair j’ai des problèmes de visualisations du phénomènes, je me lance avec ce dessin au risque de dire des bêtises
,
Pièce jointe 48686
Une couche d'épaisseur 3r autour d'une bulle de rayon r me donne une sphère de rayon 4r.
Pourquoi posé notre bulle initialement au centre ?
Si la bulle n'avançait pas, elle resterait au centre de la zone de diffusion du gaz. Dans la réalité, comme elle avance, elle sera décentrée et la zone avec du gaz diffusé sera centrée un peu plus bas que la bulle.
De plus, comme la bulle monte, elle laisse derrière elle, une zone avec du gaz diffusé (le "cône" dont je parlais dans des messages précédents).
D'autre part, il est vrai que quand on dit que la durée d'une bulle est proportionnelle à r², il s'agit du rayon initial. Et quand on dit que la zone diffusée fait 3r, il s'agit du rayon courant.
Du moins c'est comme cela que je l'interprète.
Au revoir.

.
Bonjour,
;
Il me semble que tu as complètement modifié l'énoncé du problème:
.
Par exemple:
.
1- La donnée du problème est présentée comme une diffusion d'un gaz A vers l'extérieure (le liquide) ce qui veut dire que le système est hors d'équilibre chimique avec le milieu extérieur autrement dit que le potentiel chimiquede l'espèce dans la bulle est beaucoup plus grand que le potentiel chimique de l'espèce A dans l'eau et le reste asymptotiquement (spatialement et temporellement).
.
2- Il est précisé que la bulle monte lentement, ce qui suppose que le mécanisme de diffusion l'emporte sur le mécanisme d'ascension,ce qui doit se traduire par la comparaison d'un temps caractéristique d'un temps de diffusion Td à un temps de montée de la bulle Tm.
.
Si Tm > Td alors le mécanisme "d'évaporation" de la bulle est controlée par un mécanisme de diffusion en volume. Si Tm < Td il s'agit d'un mécanisme dont la cinétique est controlée par des mécanismes de surface.
.
Dans le cas intermédiaire, celui que tu présentes comme un cone la situation est ultra compliquée puisque 'une partie des échanges sera controlée par un mécanisme de surface, 'dans la partie haute de la bulle, et l'autre partie par des mécanismes de volume dans la partie basse.
.
quand a compliquer le problème. Si la bulle monte il faut prendre en compte la baisse de pression qui sollicite la bulle à l'expansion. Et pourquoi pas tenir compte des échanges de chaleur pour tenir compte de la non adiabacité!
.
En bref faut-il considérer ce problème comme un problème scolaire, ce qu'il semble être ou discuter proprement des mécanismes physiques impliqués et donc discuter fondamentalement des hypothèses?

"La couche avec du gaz" !! : Tu parle de la bulle ? (Je n’y faisais pas allusion)
Lorsqu’elle sera décentrée, je n’aurais plus une épaisseur 3r de liquide entourant ma bulle
Elle peut soit montée soit descendre ? (Zones vierges)
Je crois comprendre l’histoire du « cône » ?: tu faits allusion à la superposition (r diminue) des espaces saturé en gaz (se trouvant sous les traces [laisser]de l’ascendances de la bulle)
Je pensais que l’épaisseur de la couche liquide ne variait pas
C'est bien ça,
A prioris c’est ça, c’est censé être tout juste une application aux lois de flux de diffusion,rien de plus
Si tu as une petite idée, peut tu nous faire un petit schéma explicatif qui me permettrais d’y voir enfin plus clair et d'arriver au résultat
Un petit coup de pouce
A+


Re.
La couche de liquide entourant la bulle avec du gaz qui a diffusé.
Si la bulle n'avançait pas, elle resterait au centre de la zone de diffusion du gaz. Dans la réalité, comme elle avance, elle sera décentrée et la zone avec du gaz diffusé sera centrée un peu plus bas que la bulle.
Je connais UN cas dans lequel une bulle peut descendre au lieu de monter. C'est un cas très spécial. Mais c'est un gars qui avait fait sa thèse sur les bulles qui me l'a raconté. Je ne crois pas que beaucoup de gens connaissent des cas où les bulles descendent (il faut qu'elles se déplacent contre la poussée d'Archimède).
C'est bien cela.
Tel que je comprends la phrase, l'épaisseur de la couche est égal à 3r, avec r le rayon courant. Mais c'est mon interprétation d'une hypothèse que je ne trouve pas vraisemblable. Je ne parie même pas un café dessus.
Mais je vous ai déjà dit. Je ne sais pas quelles hypothèses on est censé faire. Si je le savais je vous l'aurais déjà dit.
A+

Si j’ai posé cette question c’est pour savoir si la partie (de la couche liquide) en contre bas de la bulle, (l’autre moitié) sera saturé ou bien restera vierge en gaz ? puisque la bulle ne diffuse que vers le haut !!Je connais UN cas dans lequel une bulle peut descendre au lieu de monter. C'est un cas très spécial. Mais c'est un gars qui avait fait sa thèse sur les bulles qui me l'a raconté. Je ne crois pas que beaucoup de gens connaissent des cas où les bulles descendent (il faut qu'elles se déplacent contre la poussée d'Archimède).


Bonjour.
Je crois que vous confondez diffusion et flottabilité. Le gaz diffuse dans toutes de directions et n'est pas influencé par la pesanteur. Par contre la bulle monte car sa densité est plus faible que celle du liquide et la poussée d'Archimède la fait monter.
La couche en dessous de la bulle contient du gaz. Non seulement parce que le gaz diffuse dans toutes les directions, mais parce que, quand la bulle monte, c'est la couche de liquide qui était sur les côtés qui prend la place libérée par la bulle.
À mesure que la bulle monte, le liquide "s'écarte pour la laisser passer" et se referme derrière son passage. Et le gaz diffuse sur ce liquide qui s'écarte et se referme.
Au revoir.

Salut,
Oui, oui je vois,Je crois que vous confondez diffusion et flottabilité. Le gaz diffuse dans toutes de directions et n'est pas influencé par la pesanteur. Par contre la bulle monte car sa densité est plus faible que celle du liquide et la poussée d'Archimède la fait monter.
La couche en dessous de la bulle contient du gaz. Non seulement parce que le gaz diffuse dans toutes les directions, mais parce que, quand la bulle monte, c'est la couche de liquide qui était sur les côtés qui prend la place libérée par la bulle.
À mesure que la bulle monte, le liquide "s'écarte pour la laisser passer" et se referme derrière son passage. Et le gaz diffuse sur ce liquide qui s'écarte et se referme.
Mais donc la ..
C'est-à-dire même si la bulle restait au centre (ce qui n’est pas le cas ), la diffusion pourrait normalement avoir lieu,
la zone autour de la bulle va bien se saturé, mais par suite le gaz (à partir de la) va continué à diffuser vers les zones vierges!!,
La diffusion est donc indépendante du déplacement ou non de la bulle,
Bref, je me suis un peu dispersé,
A+


Re.
Dans la réalité, même si la bulle ne bougeait pas, il y aurait diffusion car la diffusion suit ses propres règles et ne s'arrête pas à 3r. Mais si la bulle n'avançait pas ET que la diffusion s'arrêtait à 3r, une fois cette zone saturée, la diffusion s'arrêterait.C'est-à-dire même si la bulle restait au centre (ce qui n’est pas le cas ), la diffusion pourrait normalement avoir lieu,
la zone autour de la bulle va bien se saturé, mais par suite le gaz (à partir de la) va continué à diffuser vers les zones vierges!!,
La diffusion est donc indépendante du déplacement ou non de la bulle,
A+

Entendu,
La , la bulle avance la diffusion arrive à terme après avoir saturé une épaisseur 3 r0
-Pour l’instant je arrive pas à caserla donné : couche liquide d’épaisseur 3r,
Je peux écrire :
L’expression du flux de diffusion
: masse volumique du gaz,
Conservation de la matière(à chaque instant t) :
Avec:
r : rayon courant , r0 : rayon initial,
(surface de la bulle [sphére] à t]
J’irais pas bien loin!!,
?
A+


Re.
Non. Vraiment pas. La formule de diffussion est:
Et ce qui compte est le gradient de la concentration 'n' et non la masse volumique du gaz.
Le terme JSt n'est pas bon, car pendant la durée du phénomène, J et S on changé en permanence.
Vous pourriez essayer la forme différentielle et dire que pendant un temps dt la quantité de gaz qui est sorti est JSdt et que ceci donne une diminution du rayon dr:
Mais vous n'êtes pas plus avancé pour autant. De toutes façons vous ne connaissez pas ni la concentration 'n' ni son gradient. Dans la réalité elles changent avec le temps. Quand la bulle arrive en contact avec une zone sans gaz diffusé, le gradient est très grand et le gaz diffuse très vite. Mais à mesure que le gaz diffuse, le gradient diminue et le gaz diffuse de plus en plus lentement sans jamais s'arrêter.
L'hypothèse des 3r était censée simplifier cette situation. Mais je n'ai pas trouvé comment.
A+

A bon!!,
si si on a bien l’habitude d’écrire ça,
Exemple: http://www.utc.fr/~houde/TF11/ch4a.html
Oui,je ne suis pas contre , mais précise juste à quoi est égal la surface S,
C'est une enigme....
A+


Re.
Vous confondez la masse volumique DU gaz avec la masse volumique DE gaz dans le liquide, qui est la concentration (à un facteur près).
La masse volumique DU gaz est sa densité: 1,3 kg/m3 pour l'air.
La masse volumique DE gaz est la concentration qui, elle, est (très) variable.
Le fait que dans votre lien on utilise la lettre rhô (souvent utilisée pour la densité ou masse volumique), ne fait qu'ajouter à la confusion.
La surface est la surface à travers laquelle on a une densité de courant égale à J. Si le problème avait une symétrie sphérique, la surface serait une sphère (de rayon égal à celui utilisé pour calculer J), mais ce n'est pas le cas.
Au revoir.

Oui, oui effectivement, j’ai fait l’erreur d’utiliser la même variable pour décrire la masse volumique du gaz et sa concentration en masse dans le liquide,Vous confondez la masse volumique DU gaz avec la masse volumique DE gaz dans le liquide, qui est la concentration (à un facteur près).
La masse volumique DU gaz est sa densité: 1,3 kg/m3 pour l'air.
La masse volumique DE gaz est la concentration qui, elle, est (très) variable.
Le fait que dans votre lien on utilise la lettre rhô (souvent utilisée pour la densité ou masse volumique), ne fait qu'ajouter à la confusion.
Merci pour la remarque LPFR,
Décidément ça se complique,
représente en quelque sorte la quantité perdue (diffusé) de gaz par unité de temps : la quantité de matière passant de la bulle (phase gazeuse) à la phase liquide, j’aurais été partant pour prendre S : la surface de la bulle courante (interface) ?
A+


Re.
Oui, bien sur, et vous auriez eu raison. Le problème est qu'on ne connaît pas le gradient de la concentration à cet endroit (et il change tout le temps).Envoyé par Kley;1745893 [TEX
J \cdot S[/TEX] représente en quelque sorte la quantité perdue (diffusé) de gaz par unité de temps : la quantité de matière passant de la bulle (phase gazeuse) à la phase liquide, j’aurais été partant pour prendre S : la surface de la bulle courante (interface) ?
En écrivant ceci je viens d'avoir une idée. Et si la petite phrase à propos de 3r était donnée pour calculer ce gradient? C'est à dire que le gradient serait la concentration dans la bulle (cette fois on pourrait utiliser la densité DU gaz) divisée par 3r. Je ne trouve pas beaucoup de sens à cette idée, pas plus de dire que la diffusion s'arrête à 3d. Mais avec ça, la densité de courant devient constante et vous pouvez écrire l'équation de conservation de matière comme vous l'aviez fait, mais avec J et le gradient constant cette fois. Seule S changerait avec le rayon de la bulle.
Essayez avec ça. Qui sait!
Je viens d'essayer. Ça marche! Je trouve:
Mais je trouve toujours que l'hypothèse n'a pas de logique.
A+

Oui ,oui en prenant l'epaiseur de 3r0 , je trouve bien :,
OK,
Il y a juste une deuxième question,(je ne l’avais pas posté pensant qu’en répondant à la première je pourrais répondre à la seconde seul , finalement.. .)
On a mesuréet on a trouvé qu’il était égal à 25. 10-9
Calculer la valeur de la diffusivité D du gaz dissout dans le liquide connaissant la valeur du coefficient de partage m=0,5 (concentration dans le gaz divisé par l’interface coté liquide)
Je ne vois plus !! Et puis je pourrais directement calculer D à partir de l’expression trouvée !!!!
?
A+


Re.
Oui, j'ai bien pris 3r et non 3r0.
J'imagine que d0 doit être soit le diamètre soit le rayon de départ des bulles et t la durée. Et t ce que nous appelons tf.
Donc on peut déduire D.
Pour l'utilisation du coefficient de partage, j'interprète que le gradient n'est pas
mais
.
Donc il faut refaire le calcul en ajoutant le ½ aux bons endroits.
A+

Oui le diamétre initial,
Oui,
MAIS m=0,5 ; tu trouve censé que la concentration interfaciale du coté gaz soit inférieur à celle du coté liquide alors que la diffusion se fait dans ce sens (Gaz vers Liquide)!!!
Donc:
, je trouve D=1,875 . 10-8 m2/s
Je suis censé trouver D=1,302 . 10-9 m2/s ?
mais c’est mieux que rien,
A+


Bonjour.
Je pense qu'il faudrait relire la définition de "coefficient de partage".
En regardant la valeur, il me semble invraisemblable que la concentration de molécules de gaz dans le liquide soit égale à la moitié de la concentration dans le gaz. Cela correspondrait à une solubilité du gaz énorme. La solubilité de l'azote en masse n'est que de 0,00003, et celle du CO2 de 0,0033. Il n'y a que des choses comme le NH3 qui ont des solubilités de 0,5.
Au revoir.

Salut
Si ce n’était que ça, c’est encore pire:
Regarde l'enoncé,
"La valeur du coefficient de partage m=0,5 (Concentration dans le gaz divisée par la concentration à l’interface coté liquide)"
ça voudrait dire que la concentration du gaz dans le liquide est égal au double de la concentration dans le gaz !!!!!!!!!!!!!!
A+


Re.Si ce n’était que ça, c’est encore pire:
Regarde l'enoncé,
"La valeur du coefficient de partage m=0,5 (Concentration dans le gaz divisée par la concentration à l’interface coté liquide)"
ça voudrait dire que la concentration du gaz dans le liquide est égal au double de la concentration dans le gaz !!!!!!!!!!!!!!
Ce serait peut-être possible avec de l'ammoniaque. Il est surprenant que l'on donne un exercice avec un cas si extrême. Mais vous avez raison qu'à la place de ½ c'est un 2 qu'il fallait mettre.
Mais c'est vous qui avez les cours et qui peut regarder la définition du terme.
A+

Même si ce cas est extrême il ne doit pas pour autant dévier du principe même de la diffusion, la j’ai l’impression que c’est le cas (je me trompe ?),
On est dans le cas de dissolution d’un gaz, comme on a pu le voir une quantité de gaz diffuse de la bulle de gaz pour pénétrer dans le liquide, pour que ceci puisse se faire il est impérative qu’a l’interface : on est une concentration du coté gaz supérieur à celle du coté liquide,
Car comme tu l’as dit sur une précédente discussion :
Alors que dans cette exo,à l'interface : C (gaz) du coté liquide =2 C (gaz) du coté gaz
Qu’est-ce que t’en pense?
A+


Re.
Oui, mais le cas de l'ammoniaque n'est pas de la simple diffusion. Le NH3 ne se limite pas à diffuser dans l'eau: il réagit pour former de l'ammoniaque. À 20°C la solubilité est d'environ 0,5 g de gaz par gramme d'eau. Ce n'est pas encore le 2 du problème mais c'est déjà beaucoup. Mais le gaz n'est pas vraiment en solution dans le liquide. Il n'en reste que très peu de NH3 dans l'eau.
Mais il est vrai que la diffusion se fait toujours du plus concentré à moins concentré. Un m < 1 ne permet pas la diffusion.
C'est pour cela que je pense que la définition de m n'a pas été bien comprise. En Wikipedia on donne la définition pour un soluté entre deux phases. On peut peut-être considérer qu'une des deux phases est le gaz lui-même. Mais la valeur me turlupine. Relisez le cours et l'énoncé. Vous avez peut-être raté LE détail important.
Si non je ne sais pas quoi faire.
A+

S’il y a réaction chimique je n’maitrise pas,
Dans le cas de la diffusion entre phase gazeuse et liquide,C'est pour cela que je pense que la définition de m n'a pas été bien comprise. En Wikipedia on donne la définition pour un soluté entre deux phases. On peut peut-être considérer qu'une des deux phases est le gaz lui-même. Mais la valeur me turlupine. Relisez le cours et l'énoncé. Vous avez peut-être raté LE détail important.
generalemet on travail à l’interface (équilibre) avec la loi d’Henry P = H C
P : pression partielle du gaz (Phase gazeuse)
C : concentration du gaz dans la phase liquide
H : coefficient d’Henry ,qui est un peu l’équivalent de ce cœfficient de partage m,
Quand H petit : soluble,
H grand : peu soluble,
Pour l’exercice, j’ai recopié exactement l’énoncé et m est présenté comme étant le quotient des concentration interfacial (gaz/liquide),
Donc je ne vois pas non plus pourquoi m=0,5?
A+

