Salut à tous,
Voici comment se présente mon probléme:
Des bulles d’un gaz pur de rayon r sont injectées dans un liquide dans lequel elles montent très lentement en diminuant de volume du fait de la dissolution du gaz dans le liquide. On observe que le temps de dissolution complète de la bulle « t » est proportionnel à r2
Justifier ceci théoriquement en supposant le régime stationnaire et en négligeant la convection.
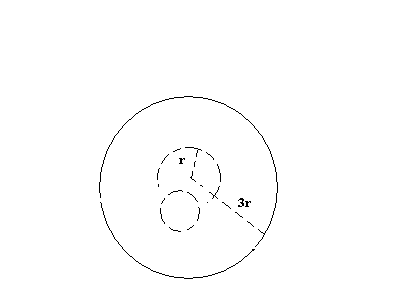
La couche de de diffusion en phase liquide à une épaisseur égal à 3r.
Merci
Ciao
-----









 !!!!
!!!!
 ,
, , je me lance avec ce dessin au risque de dire des bêtises
, je me lance avec ce dessin au risque de dire des bêtises