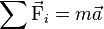[Physique-Mecanique]Equation parametrique d'un pendule simple

[inviteb8dd143b]

Bonjour tout le monde,

Je demande ici votre aide car j'ai un petit problème pour trouver l'équation paramétrique d'un pendule simple oscillant.

Voila le schéma:



J'etudie les forces:

référentiel : terrestre
Système étudiés : balle de masse "m"
bilan des forces:
-Poids: vers le bas, parallèle au vecteur g, P=m*g
-Tension: vers le haut, parallèle au fils , de même valeur que le poids

J'applique donc la seconde loi de newton:





On projette sur (O_x) et sur (O_y):
soit a correspond d a l'angle.
(O_x)

-P_x=m*a_x
=>-sin(a)*P=m*a_x
=>-sin(a)*g=a_x

(O_y)

T-P_y=m*a_y
=>(m*g)-cos(a)*P=m*a_y
=>g-cos(a)*g=a_y

On intègre par rapport au temps

==> a_x=d_vx/d_t
==> a_y=d_vy/d_t

donc:

Vx(t)=(-sin(a)*g)(t) + Vx(0)
Vy(t)=(g-(cos(a)*g))(t) + Vy(0)

ce qui revient a dire si on intègre un nouvelle fois par le temps.

avec X₀=(L-cos(a)*L) ou L est la longueur du fil.

avec Y₀=(sin(a)*L) ou L est la longueur du fil.


Malheureusement, lorsque l'essai de modéliser ces deux courbes sur ma calculette sa ne marche pas

Pouvez vous m'expliquer pourquoi.

Merci
-----

[marsan09]

bonjour,
avec une figure on pourrait essayer de comprendre,
mais les résultats dans lesquels les vitesses sont proportionnelles à t2, ça me parait très faux.
Ce n'est pourtant pas pour cela que les courbes ne s'affichent pas.

[vaincent]

Bonjour,

lorsque tu projettes sur (Oy) tu écris T=m*g alors que c'est T=k*x, avec module de k*x qui vaut m*g ce qui te permet de déterminer la valeur de k, le tension du fil. Mais il faut bel et bien garder T= k*x.

De plus la tension du fil a forcément une composante suivant (Ox) mais certainement pas le poids.

On obtient alors des équations du 2nd ordre dont les équations caractéristique sont de la forme R²+(k/m)=0. Les solutions sont du type sinusoïdale : système oscillant.

[inviteb8dd143b]

Bonjour tout le monde,

merci pour vos réponses.

Pour répondre à marsan09, j'intègre en fait un seconde fois par le temps donc le (t) de la vitesse devient (t^2) pour la position dans l'espace (c'est en fait la primitive de t, car V_x=dx/dt).


vaincent dans la tension s'exprime par T= k*x dans le cas d'un ressort, pas dans le cas d'un pendule.

Après discussion avec mon prof de physique, il me conseille de passer par le repère de Frenet.

Voila

[A voir en vidéo sur Futura]

[inviteb8dd143b]

Voila le schéma qui avait mal été uploadé:

Le schéma:

[inviteb8dd143b]

Comment qu'on fait pour modifier un post precedent.

L'angle têta est à la jonction entre le vecteur P et l'axe Oy