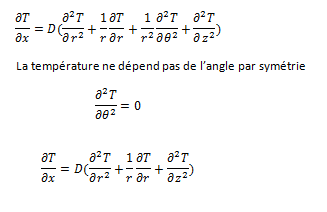Equation de chaleur et symetries

[invite866905d6]

Bonjour,

Je souhaite etudier la diffusion de chaleur dans un cylindre de Diametre D=50mm et de longueur L=150mm. Le cylindre est chauffe par induction dans sa partie haute sur une hauteur de 40mm a 800°C.

N'ayant pas d'outils pour l'analyse par elements finis a ma disposition, je me dis qu'il doit etre relativement simple d'etudier une section du cylindre et d'etudier la diffusion par differences finis en effectuant une resolution sous matlab. Ma question n'est pas relative a la discretisation du probleme et a la resolution technique mais plutot a la fiabilite du modele.

L'equation de chaleur est:
0c116758480c1611ab5a7ff7626e4fea.png


Je prend P=0 et je dis que la production de chaleur est suffisante pour considerer que dans la partie haute du cylindre la temperature est a tout moment egale a 800°. D'autre part je n'etudie qu'une section du tube et donc de ne considerer que les derivees secondes par rapport a x et y. Je me ramene donc a un probleme plan en disant que la chaleur ne se diffuse que dans un plan. Cette methode peut elle fonctionner? J'ai un doute car cela revient a negliger la conduction dans la direction z.

Cependant vu la symetrie cylindrique du plan il doit bien y avoir un moyen de modeliser cela simplement en 2D non? Eventuellement en utilisant les coordonnes cylindriques?

Autre question: en pratique on abouti a une solution asymptotique, c'est a dire que la repartition de chaleur n'evolue plus au bout d'un certain temps. Mais en modelisant le probleme avec mes hypotheses, la temperature va toujours evoluer jusqu'a ce que la temperature soit partout homogene non?

Merci de votre aide!
-----

[phys4]

Bonjour,

La position du cylindre n'est pas précisée. Si nous le supposons posé sur sa base circulaire, la partie haute chauffée à 800° est une portion du cylindre.

Le problème se réduit à une propagation à une seule dimension? Dans le sens z, toutes les sections circulaires du cylindre ont une température constante T(z,t)

Bien sur cela tendra vers une température homogène.

[inviteb836950d]

...Je me ramene donc a un probleme plan en disant que la chaleur ne se diffuse que dans un plan. Cette methode peut elle fonctionner? J'ai un doute car cela revient a negliger la conduction dans la direction z.

Sauf si ton plan est longitudinal (c-à-d. contient z).

[inviteb836950d]

et même un demi plan puisque aucun flux ne traverse l'axe z ...

[A voir en vidéo sur Futura]

[invite866905d6]

Je ne comprend pas trop, je fais une section selon le plan XY comme le montre l'image suivante:

XXXXXXXXXXXXXXX

La partie chauffee est en effet donc une portion de cylindre. Mon plan est donc bien longitudinal, mon raisonnement de fonctionne donc pas en ne considerant que la diffusion selon Z et X?

Y a t-il un moyen de se ramener en un probleme 2D avec une section de ce type (ie on veut etudier la diffusion de chaleur sur le longueur du cylindre) ?

[invite866905d6]

(La partie en rouge est toute la partie chauffee a 800°).

[obi76]

Bonjour,

l'hébergement d'image sur serveur externe est interdit. La prochaine fois je supprimerai sans prévenir.

Pour la modération,

[phys4]

Il s'agit bien d'un problème 1D, il suffit de considérer la propagation dans le sens de l'axe.

Je pense que vous n'aurez pas de difficultés.

[invite866905d6]

Ne serait-ce pas un problème 2D? Dans le plan de coupe de l'image, il y a bien propagation selon z et x non? Et donc je dois considérer les dérivées secondes de T selon x et z?

Si oui, comment justifier qu'on ne tient pas compte de la propagation selon "la profondeur" y?

@Obi76, merci d'avoir modifié mon message.

[inviteb836950d]

Ne serait-ce pas un problème 2D? Dans le plan de coupe de l'image, il y a bien propagation selon z et x non? ...

oui, il me semble.
le plan intéressant est le plan entre z=0 et l (longueur du cylindre) et x=0 et d/2 (d=diamètre du cylindre)
reste à fixer les conditions au limites (par ex 800°C en z=0...et la température en x=d/2).

(je faisais ça les doigts dans le nez y-a qlq années, mais je sais plus faire...)

[invite866905d6]

Merci.
Oui pas de problème pour les conditions aux limites.

J'aimerais néanmoins comprendre pourquoi on peut dire que la propagation selon y n'intervient pas dans le gradient de température qu'on obtiendra dans le plan de coupe considéré?

[inviteb836950d]

Merci.
Oui pas de problème pour les conditions aux limites.

J'aimerais néanmoins comprendre pourquoi on peut dire que la propagation selon y n'intervient pas dans le gradient de température qu'on obtiendra dans le plan de coupe considéré?

je ne comprends pas ta question...
x et y sont dégénérés.
la diffusion suivant x est la même suivant y ou toute combinaison linaire de x et y.

[invite866905d6]

Si je programme mon problème 2D je vais tenir compte de la diffusion selon Z et X.

Or en réalité, la diffusion se fait dans les trois directions. Je me dis donc qu'en étudiant que le problème selon Z et X il y a "trop" de chaleur qui va se propager dans ce plan (puisqu'en réalité il y a aussi une partie de chaleur qui va dans la direction Y). Enfin je ne sais pas si je me fais bien comprendre, peut être que je me pose des questions pour rien mais cela ne me semble pas si évident de point de vue fiabilité du modèle.

[invite866905d6]

Personne pour un petit éclaircissement ?

[phys4]

Ne serait-ce pas un problème 2D? Dans le plan de coupe de l'image, il y a bien propagation selon z et x non? Et donc je dois considérer les dérivées secondes de T selon x et z?

Si oui, comment justifier qu'on ne tient pas compte de la propagation selon "la profondeur" y?

@Obi76, merci d'avoir modifié mon message.

J'ai pensé que vous alliez finir facilement, pourquoi voulez vous absolument que ce soit un problème 2D :
Il existe seulement une variation de température suivant z au début, la symétrie cylindrique implique que toutes les sections sont identiques.

Pourquoi apparaitrai t-il un gradient et une propagation selon les deux autres directions ?

[invite866905d6]

La diffusion ne se fait pas que selon l'axe z. Selon l'axe x il y a forcément aussi diffusion. Je souhaite aussi étudier la diffusion de la chaleur dans l'air à gauche et à droite de cette section du cylindre (pour avoir une idée de la température à laquelle je me retrouverai à une distance x du cylindre). Evidemment, cela implique de mettre les bonnes conditions de Dirichlet, Neumann, de masse volumique et de conductivité, mais cela n'est pas le problème.

Pour moi si on peut simplifier le problème il s'agit au mieux d'un problème 2D.

[phys4]

Ton énoncé original ne mentionne pas de pertes latérales, seulement la diffusion de chaleur à l'intérieur du bloc.

Si tu ajoutes une équation de pertes latérales, alors oui, il faut utiliser la symétrie cylindrique pour ne garder que deux coordonnées z et r pour le rayon et travailler en coordonnées polaires.

[invite866905d6]

Merci de votre aide. En effet je n'avais pas précisé que je souhaité étendre le problème.

Cela donnerait donc:


Cela serait donc un problème entièrement déterminé par cette équation dans les deux directions x et z.

Cela vous être bon?

[phys4]

Tout va bien, si ce n'est que la variable temps s'appelle x maintenant. Ce n'est pas une faute, seulement un choix personnel autorisé.

[invite866905d6]

Merci bien. C'est plutôt une faute d'inattention de ma part, c'est bien plus logique de laisser 't' pour la variable temps

Bonne journée à vous.