Cone de lumière et hypersphère

[sephirot2010]

Bonjour à tous,

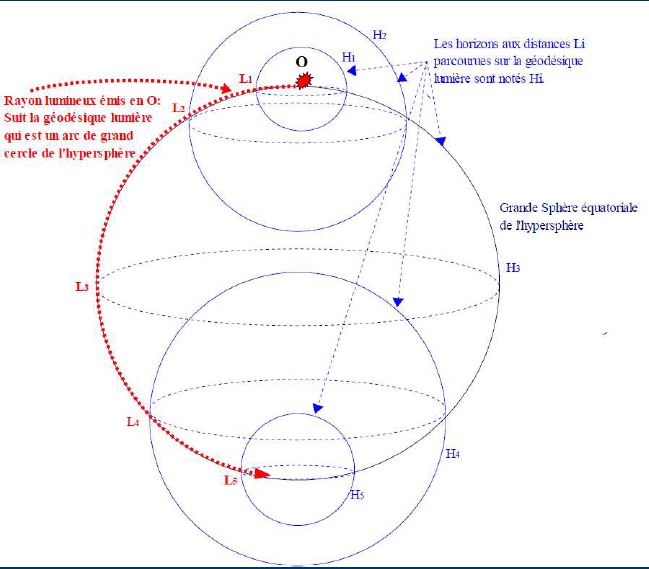
En relativité restreinte, on a l'habitude de représenter un événement de l'espace-temps de Minkowsky par un cône de lumière. En faisant cela, on réduit les 3 dimensions spatiales à seulement deux et la dimension perpendiculaire à l'espace est celle du temps. Voilà ma question : est-ce que quelqu'un a déjà pensé à "représenter" un événement comme une hypersphère 4D, ce qui permettrait de conserver dans la représentation les 3 dimensions d'espace tout en introduisant bien la 4eme (le temps) ? Si cela a été fait, est-ce que vous auriez des sources (bouquin, articles,etc...). Si non, qu'est-ce que vous pensez de l'idée ?

Merci.
-----

[inviteb7558fdc]

L'événement en question ne se situerait-il pas plutôt à l'intérieur d'un hypercône? (un événement n'est pas une hypersphère mais un point (x0,x1,x2,x3) dans l'espace-temps)

[Amanuensis]

En relativité restreinte, on a l'habitude de représenter un événement de l'espace-temps de Minkowsky par un cône de lumière.

?? Non... Un événement est un "point" de l'espace-temps modélisé comme variété 4D. À chaque événement est associé un cône de lumière, dont l'événement est le sommet.

En faisant cela, on réduit les 3 dimensions spatiales à seulement deux et la dimension perpendiculaire à l'espace est celle du temps.

??? Doit y avoir confusion avec autre chose que ce qu'on appelle en RR un cône de lumière.

[sephirot2010]

Oui, j'aurais du mieux formuler ma question : est-ce que l'analogue du cône de lumière (avec deux coordonnées d'espace + celle du temps) est une hypersphère (avec 3 coordonnées d'espace + 1 de temps) ?
Merci.

[A voir en vidéo sur Futura]

[inviteb7558fdc]

Je le répète, c'est un hypercône...
comment pourrait-on passer d'une surface définie par (x1^2+x2^2)^1/2=x4 (formule du cône en 3D) à (x1²+x2²+x3²+x4²)=1 (formule d'une hypershpère en 4D)...non : la généralisation est (x1^2+x2^2+x3^2)^1/2=x4, qui est la formule d'un hypercone de revolution autour de l'axe x4.

[inviteb7558fdc]

ps : la formule d'hypershpere que j'ai donnée est celle d'une hypersphere 4D plongée dans un espace 5D. Pour une hypersphere "spatiale" plongée dans un "espace" temporel comme tu le voudrais, ce serait (x1^2+x2^2+x3^2)=x4^2

[sephirot2010]

Je ne comprends pas cette histoire d'hypercône.
La représentation, dans la RR, du cône de lumière correspond, si je ne me trompe, à la réduction à 2 coordonnées d'espace + une de temps de la propagation d'un flash lumineux issu du sommet du cône (événement). Maintenant, si je considère dans un premier temps la propagation de ce flash lumineux dans l'espace 3 D (sans le temps) on est d'accord qu'il le fait selon une nappe sphérique ? Bon, bah si je veux ajouter ensuite la dimension temporelle, j'ajoute une quatrième dimension orthogonale à ma sphère et j'obtiens bien une hypersphère, non !?

[Amanuensis]

Oui, j'aurais du mieux formuler ma question : est-ce que l'analogue du cône de lumière (avec deux coordonnées d'espace + celle du temps)

???, encore. Un (pas le) cône de lumière est une notion 4D, c'est l'union des trajectoires de genre lumière (disons des trajectoires suivi par un "photon") passant par un même événement. On peut effectivement repérer un point (un événement) d'un cône avec trois coordonnées, deux donnant la direction spatiale (un point de la sphère céleste) et la troisième une durée (0 pour l'événement sommet, positive pour les parties futures des trajectoires et négative pour les parties passées.

(Au passage, ce qu'on voit --à un instant donné-- est la partie passée du cône de lumière dont l'oeil (pris à l'instant donné) est le sommet. Et "l'usage" est de s'y repérer avec 3 coordonnées spatiales...)

est une hypersphère (avec 3 coordonnées d'espace + 1 de temps) ?

?? L'analogue à quel sens ??

(Par ailleurs la notion d'hypersphère ne va pas avec de telles notions de coordonnées. C'est en général une notion de géiométrie euclidienne -- l'ensemble des points à une même distance euclidienne d'un centre. Il y a aussi une notion plus faible, topologique, mais alors on ne s'occupe même plus de coordonnées...)

[Amanuensis]

La représentation, dans la RR, du cône de lumière correspond, si je ne me trompe, à la réduction à 2 coordonnées d'espace + une de temps de la propagation d'un flash lumineux issu du sommet du cône (événement). Maintenant, si je considère dans un premier temps la propagation de ce flash lumineux dans l'espace 3 D (sans le temps) on est d'accord qu'il le fait selon une nappe sphérique ?

Oui. Pour un cône donné, à chaque instant futur ou passé correspond une "nappe sphérique".

Bon, bah si je veux ajouter ensuite la dimension temporelle, j'ajoute une quatrième dimension orthogonale à ma sphère et j'obtiens bien une hypersphère, non !?

Non. La "dimension temporelle" est déjà incluse dans la description précédente : le diamètre de la nappe + le signe (selon qu'on est dans le passé ou le futur) est la coordonnée temporelle. On ne peut pas l'ajouter, puisqu'elle est déjà là, même si elle est "cachée".

C'est comme sur un cône en 3D, dont l'axe est celui des z. On peut s'y repérer avec deux coordonnées, une coordonnées de direction spatiale (l'angle dans le plan x-y) et une distance au centre. On ne peut pas "ajouter" la dimension selon "z", elle est déjà donnée (à un coefficient près) par la distance (signée).

[sephirot2010]

Bon ok, merci pour toutes ces explications. Je patauge beaucoup apparemment
Sinon, vous pourriez me dire ce que vous pensez de ce schéma où on représente la propagation du flash lumineux en utilisant l'hypersphère. Peut-être que c'est cela que j'essaie de dire sans trouver les mots et concepts corrects
Cette figure est issue d'un cours de cosmologie du Pr Edward Wright.

Merci !

[Amanuensis]

C'est pour un modèle avec espace compact ("fini") sans bord et homogène ? Dans ce cas, c'est l'espace qui est une hypersphère (une 3-sphère, la surface de la Terre étant une 2-sphère et un cercle une 1-sphère).

Et le repérage est celui que j'ai indiqué comme "l'usage", c'est à dire consistant à se repérer sur le cône par 3 coordonnées spatiales (on "ramène" à l'espace au présent) + un signe. On ne peut pas "ajouter le temps", car c'est la distance parcourue (divisée par c, si on mesure en secondes)(et signée).

Que le cône se trouve être une (double) hypersphère serait (si l'interprétation est correcte) juste une conséquence de la forme de l'espace.