Translation et rotation simultanées

[mimow]

Bonsoir tout le monde, alors après avoir donc fini la leçon du mouvement circulaire, il y a quelque trucs que je n'arrive pas encore à assimiler
complètement, parmi ces trucs, je vais en représenter un pour que je sois plus compréhensible :

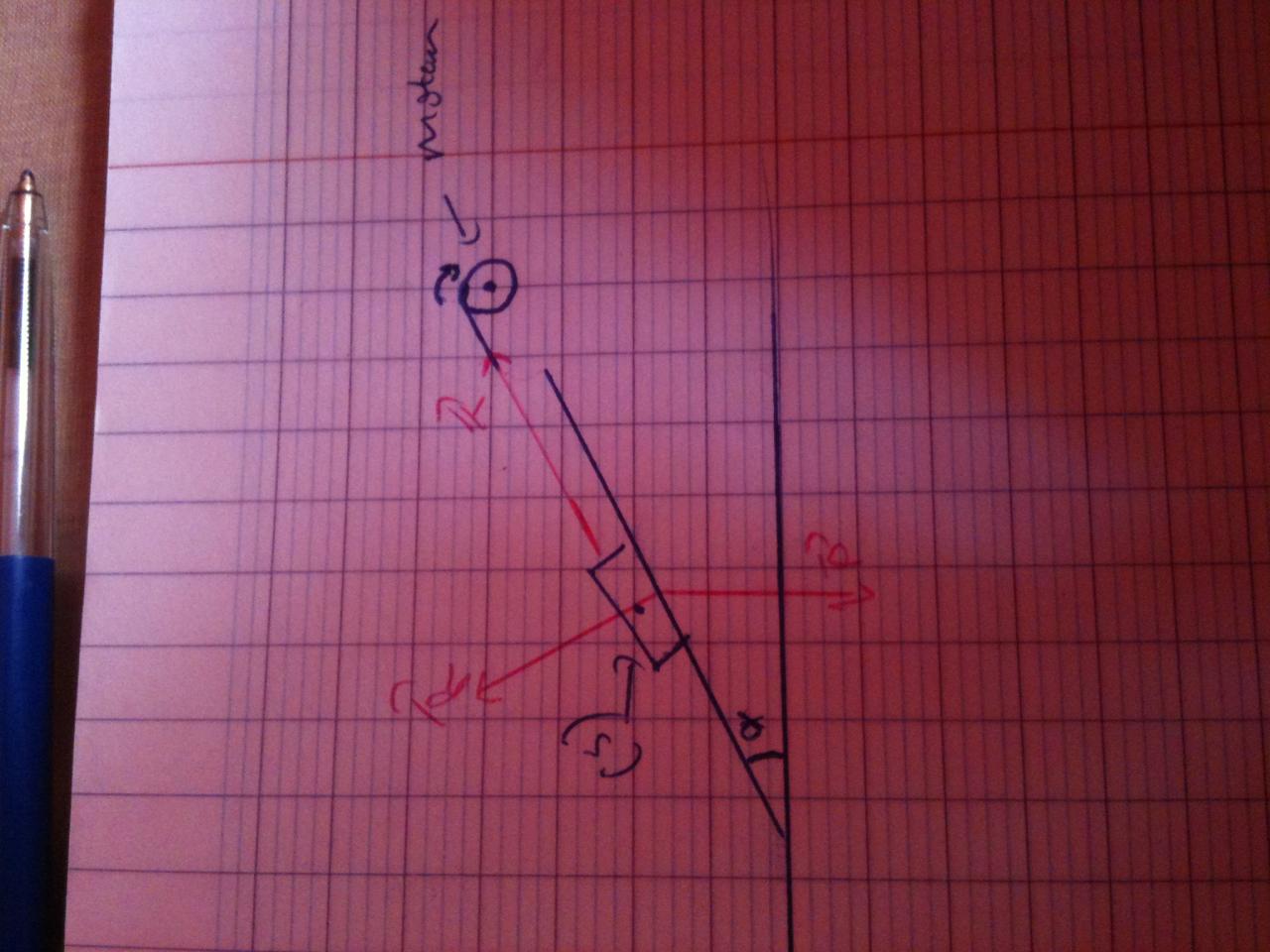
Soit un plan oblique par rapport au plan horizontale, un corps S translate sur le plan oblique et est en meme temps lié a un petit moteur par un
fil, on admet que la translation se fait vers la gauche ( soit de haut en bas ) et que le sens de rotation du moteur est l'inverse .

ma question est la suivante : pourquoi quand le moteur tourne d'un angle teta et donc d'un arc S, le corps translate d'une distance D = S ?

Si il y avait 2 corps en translation et que l'un translatait avec une distance D alors il est logique que le 2eme translatera aussi avec la meme
distance, mais ici je n'arrive pas a comprendre comment l'arc correspond a une distance de translation rectiligne .

J'espère que j'ai bien expliqué mon embarras, et merci d'avance pour les intervenants !
-----

[LPFR]

Bonjour.
Je n'ai pas compris la géométrie et le mouvement de S.
Je ne vois pas où se situe le moteur et comment l'objet S est "lié" au moteur.
Pouvez-vous faire un petit dessin ?
Au revoir.

[mimow]

Oui bien sur LFPR voici le dessin :


Je reformule ma question : je comprends pas le phénomène suivant : pourquoi quand un point M' du moteur se déplace d'un arc A, un point M de
l'objet translate d'une distance D EGALE a A .

Voila, merci pour votre aide !

[LPFR]

Re.
Quand le moteur fait un tour complet, il récupère (ou lâche) une longueur de fil égale à son périmètre 2.pi.R. Et si au lieu de tourner d'un angle de 2.pi, il tourne d'un angle thêta, alors la longueur sera thêta.R, c'est à dire l'arc correspondant à l'angle thêta.
A+

[A voir en vidéo sur Futura]