Vecteur d´onde (réflexion dans un cristal)

[Bartolomeo]

Bonjour,

je ne comprends pas trés bien la différence de phase d´une onde qui est diffractée par un cristal. (C´est dans le Kittel p. 33 7. éd. Dunod)
Si k est le vecteur d´onde de l´onde entrante et k' celui de l´onde diffusée. La différence de phase totale est exp((k - k')*r) d´après le bouquin. Pourquoi la différence de phase de l´onde diffusée est elle -k'*r? Il vient de où le signe moins? Dans la condition de Bragg on ajoute bien les 2 chemins, donc 2 sin(teta)= n Lambda. Pourquoi on écrit pas 4 Pi r sin(teta) / Lambda = 2 r*k = 2 r*k' pour la différence de phase totale?


Merci d´avance pour l´aide!
-----

[Bartolomeo]

98 fois affiché et personne n´a d´idée? Dois-je donner plus de précisions?

[LPFR]

98 fois affiché et personne n´a d´idée? Dois-je donner plus de précisions?

Bonjour.
Oui. Et ce matin il y en a 124. Mais le nombre continuera à augmenter au moins jusqu'à ce que un des lecteurs ait la même édition du Kittel que vous.
Car vous donnez une formule qui ne vaut strictement rien sans le dessin qui va avec. Et vous ne donnez ni le numéro de l'image ni même le nom du chapitre.
J'ai une édition qui doit dater de l'époque ou Kittel était bébé et, évidement, rien ne colle avec votre description.
Faites au moins une photo ou un scan du dessin. Pour ce type de brève citation, on ne viole pas les droits d'auteur.
Mais il n'est même pas certain que sans le "baratin" qui va avec le formules on puisse vous répondre.
Au revoir.

[Bartolomeo]

Bonjour.
Oui. Et ce matin il y en a 124. Mais le nombre continuera à augmenter au moins jusqu'à ce que un des lecteurs ait la même édition du Kittel que vous.
Car vous donnez une formule qui ne vaut strictement rien sans le dessin qui va avec. Et vous ne donnez ni le numéro de l'image ni même le nom du chapitre.
J'ai une édition qui doit dater de l'époque ou Kittel était bébé et, évidement, rien ne colle avec votre description.
Faites au moins une photo ou un scan du dessin. Pour ce type de brève citation, on ne viole pas les droits d'auteur.
Mais il n'est même pas certain que sans le "baratin" qui va avec le formules on puisse vous répondre.
Au revoir.

C´est bien ce que je craignais. Je voulais envoyer la photo à partir de google book, mais ce dessin n´était pas affiché justement à cause des droits d´auteur.
Mais bon pour les besoins de la cause une photo de mauvaise qualité fera l´affaire et comme je cite la source. Ca ne devrait véxer personne.

Figure 6 du chapitre "Réseau réciproque" du livre "Physique de l´état du solide" Charles Kittel, 7 è édition Dunod ISBN 2 10 003267 4.

Cordialement

[A voir en vidéo sur Futura]

[LPFR]

Re.
En fait, le dessin est mauvais.
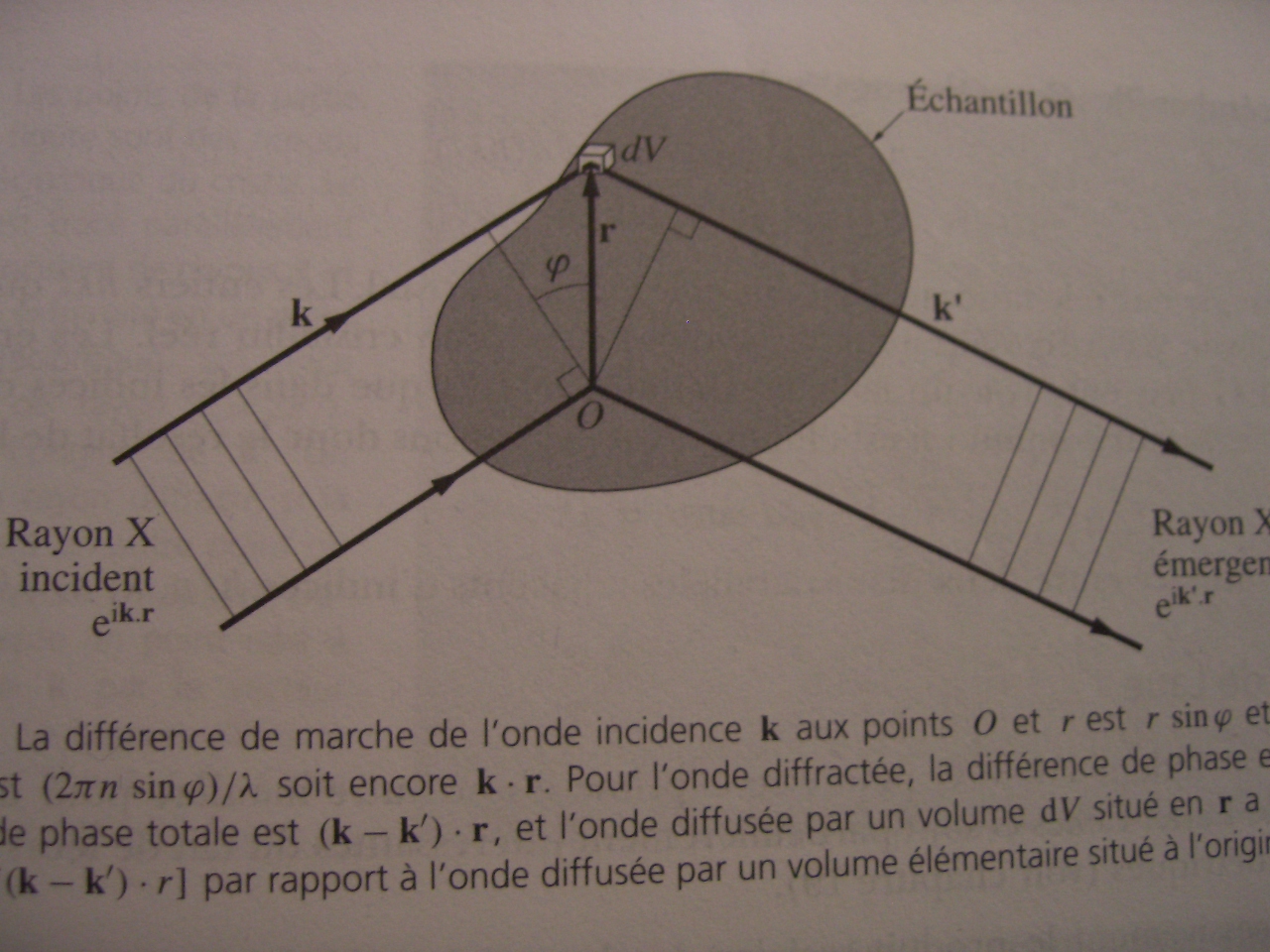
L'onde sortante ne peux pas être . Les plans "isophase" de l'onde sortante dessinés sont faux. Ils ne peuvent pas être perpendiculaires au vecteur k'.
Précisément à cause du retard de phase donné (k-k').r.

Peut-être que par la suite du texte on cherchera des plans correspondants à une interférence constructive. Mais ces plans ne correspondront pas à des rayons avec égalité de phase mais à de rayons qui ont la même phase à 2pi près.

La raison du (k - k') vient du fait que les projections de k et k' sur le vecteur 'r' ont des directions opposées. Mais dans le dessin on voit que les deux déphasages s'ajoutent.

Peut-être qu'avec le texte complet on peut comprendre la nature confuse du dessin. Mais je ne l'ai pas et on ne peut pas le publier sans enfreindre (peut-être) les droits de l'éditeur.

À propos de la condition de Bragg de votre premier post, on ajoute les deux déphasages: celui de l'onde incidente et celui de l'onde difractée. Mais les deux angles thêta ne sont pas, les mêmes. Ce n'est donc pas 2a sin(teta)= n Lambda, mais 2a (sin(thêta1) + sin(thêta2))= n Lambda
A+

[azizovsky]

Salut , soit I la projection du point O sur la droite de vecteur directeur N(i) (K(i)=kN(i)) (voir ton dessin) et J la projection de O sur la droite de vecteur directeur N(f) (avec K(f)=k.N(f) dans ta notation K(f) =K' ) et A un point appartenant au volume élémentaire dv soit les deux diffuseurs situés en deux point O et A , la différence de chemin pour les deux ondes (rayons) diffusées est IA+AJ , soit: (1) : r.cos (m) +r.cos(m') , (m=pi/2 -alpha) et m'=pi/2-m' (les angle au point A)
(1)===> R.[-N(i)] + R.N(f) = R.[N(f)-N(i)] ou R=OA (majuscule =vecteur ,min=scalaire comme /R/=r ), pour deux diffuseurs séparés par R le déphasage est donc :
(2pi/landa ).R.[N(f)-N(i)]=R.[K(f)-K(i)] . , landa =2pi/k(i)=2pi/k(f) , dans ta notation
le déphasage est r.(k'-k) .

[azizovsky]

correction : (2pi/landa).R.[N(i)-N(f)]=R.[K(i)-K(f)] d'aprés la notation du livre le diphasage est r.(k-k') il est juste

[Bartolomeo]

À propos de la condition de Bragg de votre premier post, on ajoute les deux déphasages: celui de l'onde incidente et celui de l'onde difractée. Mais les deux angles thêta ne sont pas, les mêmes. Ce n'est donc pas 2a sin(teta)= n Lambda, mais 2a (sin(thêta1) + sin(thêta2))= n Lambda
A+

Dans le contexte: le but est de démontrer la condition de diffraction, c´est à dire quand le vecteur de diffusion est égale à un vecteur du réseau réciproque, il y a diffraction:
K'-K = G. Si la diffraction est élastique on peut écrire 2K*G = G².
Si k=k' alors les angles (entre K et R noté Phi sur le schéma, entre K' et R) sont identique puisque R devient un axe de symétrie.
C´est avec g= 2Pi/d et k=2Pi/lambda qu´on retrouve la condition de Bragg. Neanmoins je ne comprends pas trop l´intéret du Kittel d´expliquer tout ca pour en revenir à la condition de Bragg.

En tout cas merci pour les explications! Et J´ai beaucoup apprécié la démonstration mathématique d´azizovsky!