discrétisation type différence fini ?

[invite9c7554e3]

Bonjour tous,

je viens vers vous car je me pose des questions sur comment discrétiser un problème afin de le résoudre...
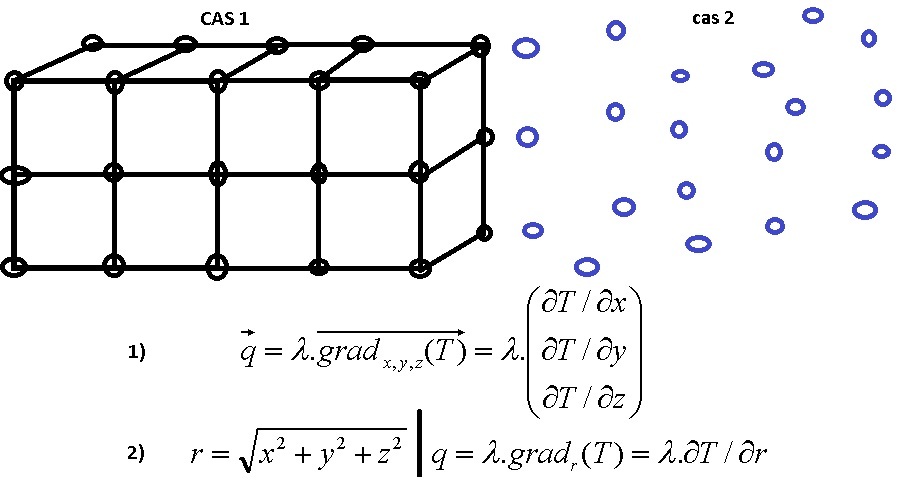
(ps : sur la figure que j'ai mis je n'utilise pas l'eq. numéroté 1mais la 2 car plus simple, je ne pense pas que ça est de conséquences)

Je m'explique sur le cas classique (cas 1 sur figure) qui ne m'intéresse pas vraiment mais qui me permettra de mieux comprendre le cas 2:
j'ai un maillage où un calcul externe a été effectué, je connais en chaque point la température (ça peut être très hétérogène comme champ)
et je voudrais calculer à présent sur plusieurs pas de temps les flux qui arrivent en chaque points du maillage connaissant les températures
des points et quel point est lié à quel autre. A partir de là j'ai une expression simple qui me permet de mettre à jour la température du point
en question, je fais ceci pour tous les points et à la fin de je met à jour une autre variable (le déplacement) qui est globale.

Pour mettre ceci en pratique, il y a plusieurs méthodes :
1) je fais une boucle sur tout mes liens entre points et je calcul le flux de chaleur qui part du point 1 ou point 2 en discrétisant
par une différence finis ma dérivée (j'utilise une variable "r" pour les coordonnées afin de ne pas avoir à faire sur toutes les compostantes)
---> c'est simple et ça à l'air de marcher super bien
2)la deuxieme solution serait de construire un schéma différence finis car je connais le pas du maillage
---> par contre pour les conditions limites je ne sais pas trop comment je pourrais faire=tout les bords sont libres
je dois donc imposer un flux nul sur chaque bord ?

que pensez vous de ces deux méthodes ? la première marche très bien mais n'est pas très orthodoxe, la seconde qui l'ai plus je n'ai pas essayé
car elle me parait pas très facile à mettre en place et je ne suis pas certain de gagner en temps de calcul (c'est ce qui m'intéresse).

Maintenant mon cas réel (cas 2 sur figure):

lorsque j'ai un maillage bien régulier j'avais le choix entre deux méthodes mais en fait dans le cas qui m'intéresse
j'ai un maillage qui peut être complètement tordu (c'est une donnée d'entrée avec laquelle je dois composer).

---> du coup le seul choix que j'ai c'est la première méthode ?
---> il n'est pas possible de faire quelque chose de plus rapide ? et/ou plus conventionnel ?

Dernière question (mais très importante):
j'ai une dernière question, je fais mon calcul pas à pas en choissisant un mais j'aimerai que ce ne soit plus un choix mais
quelque chose géré automatiquement afin de maximiser le rapport précision/tempsCalcul. Car si je fais des trop grand mes données seront peu précises
mais si je fais trop petit j'ai des temps de calculs long (et mon but c'est optimiser ceci).

---> je ne vois pas comment faire pour gérer ce automatiquement ...?
---> pour le moment j'ai dis au pas de ce diviser par 2 si la température d'un noeud varie de plus de 10% et
d'augmenter de 10% dans le cas contraire. Mais ça n'ai pas vraiment optimal car ça dépend du choix de l'utilisateur (pk 10% plutot que 20 par exemple...)

Auriez vous des choses à me conseiller ?

merci de votre aide


-----

[obi76]

Bonjour,

en différence finie, pour les conditions limites on peut mettre aussi ce qu'on veut. Flux nul : les deux derniers points sont égaux, température fixée : on fixe le dernier point...

Le truc que j'ai pas compris, c'est que tu as des points irrégulièrement disposés en tant que condition d'entrée ? Pourquoi ne pas interpoler sur un maillage régulier et utiliser une DF classique ?

PS : pour le delta T il existe une méthode toute bête (mais à respecter impérativement).

[Etrange]

Salut,

As-tu jeté un oeil sur Wikipédia pour les conditions de convergence : http://en.wikipedia.org/wiki/Courant...Lewy_condition ?
Pour les schémas usuels le CFL doit être majoré par une certaine valeur pour assurer la convergence de la simulation. Cette condition te permettra de choisir un pas de temps adapté en fonction du pas d'espace utilisé.

[invite9c7554e3]

salut tous et merci pour vos réponses !

en différence finie, pour les conditions limites on peut mettre aussi ce qu'on veut. Flux nul : les deux derniers points sont égaux, température fixée : on fixe le dernier point...

ça marche, je vais regarder, merci.

Le truc que j'ai pas compris, c'est que tu as des points irrégulièrement disposés en tant que condition d'entrée ? Pourquoi ne pas interpoler sur un maillage régulier et utiliser une DF classique ?

je ne peux pas vraiment expliquer ici... pour faire simple : je travail avec un mécanicien qui déforme son matériau/maillage
et en même temps je dois faire sur le même maillage une réactualisation de variables qui lui seront nécessaires et qui viennent
d'une résolution type thermique. (pas tout à fait ça mais je ne peux en dire plus)

PS : pour le delta T il existe une méthode toute bête (mais à respecter impérativement).

lol, pourrais tu me dire quel est ce secret ?

As-tu jeté un oeil sur Wikipédia pour les conditions de convergence : http://en.wikipedia.org/wiki/Courant...Lewy_condition ?

je t'avous que non.j'ai essayé de déchiffrer avec mon anglais pourri et j'ai pas trop compris, néanmoins ça ressemble à des conditions de stabilité
du schéma ?

Pour les schémas usuels le CFL doit être majoré par une certaine valeur pour assurer la convergence de la simulation. Cette condition te permettra de choisir un pas de temps adapté en fonction du pas d'espace utilisé.

pourrais tu me donner un exemple simple s'il te plait pour illustrer ceci ?
en différence finis je vois bien ce que c'est une condition de stabilité d'un schéma (je n'ai étudié que des cas ultra simple néansmoins en DF) mais moi ici je n'utilise pas la différence finis
(j'utilise le cas 1°) et je n'arrive pas à transposer ....

[A voir en vidéo sur Futura]

[obi76]

Pour la méthode, Etrange te l'a donné : ce sont les conditions CFL qui sont importantes :
convection : dt = C*min(dx)/max(U) (avec U la vitesse et C le CFL convectif, en général vers 0.4)
conduction : dt = C*min(dx)²*max(rho*Cp/lambda). Là si je ne dis pas de bêtises, C doit être de l'ordre de 0.1. Et (ça m'avait étonné à l'époque), même si la température est homogène, cette condition doit quand même être prise en compte, même s'il n'y a pas de flux de chaleur.

[invite9c7554e3]

c'est la première fois que je vois ce mot "CFL" j'ai regardé le lien en anglais de Etrange mais je n'ai pas tout compris, pourrais tu m'expliquer s'il te plait ce que c'est ?
et surtout pourquoi a t on besoin de les utiliser ?

merci

[obi76]

Re

lorsque tu résouds numériquement une équation différentielle, le pas de temps d'intégration possède un maximum (sauf cas particuliers, ce n'est pas le cas ici), au delà duquel la résolution diverge.

Exemple bête : tu prends une EDO linéaire du premier ordre, il y a donc une asymptote. Tu estimes la dérivée en t=0. Si le pas de temps est trop grand, alors y0 + dt*y'(t=0) sera en dehors de l'intervale d'existence des solutions (ce qui n'est mathématiquement pas possible), et ta solution oscille pour finir par faire n'importe quoi.

Que tu résolves un problème 2D ou 3D (ou ND) la condition qui t'assure la stabilité et la robustesse de ton modèle s'appele le CFL (de Courant-Friedrichs-Lewy) qui sont spécifiques au type d'équation résolue. La convection c'est du premier ordre, la diffusion / conduction c'est du second ordre, donc une condition CFL par problème résolu (et évidement, tu prends le plus restrictif).

[invite9c7554e3]

merci Obi,
dans le cas ou je résouds par DF il faudrait donc je j'utilise ce critère mais par contre dans où je n'ai pas
un maillage structuré je ne peux pas utiliser les DF et donc ce critère sur le pas de temps ??