Bonsoir ;
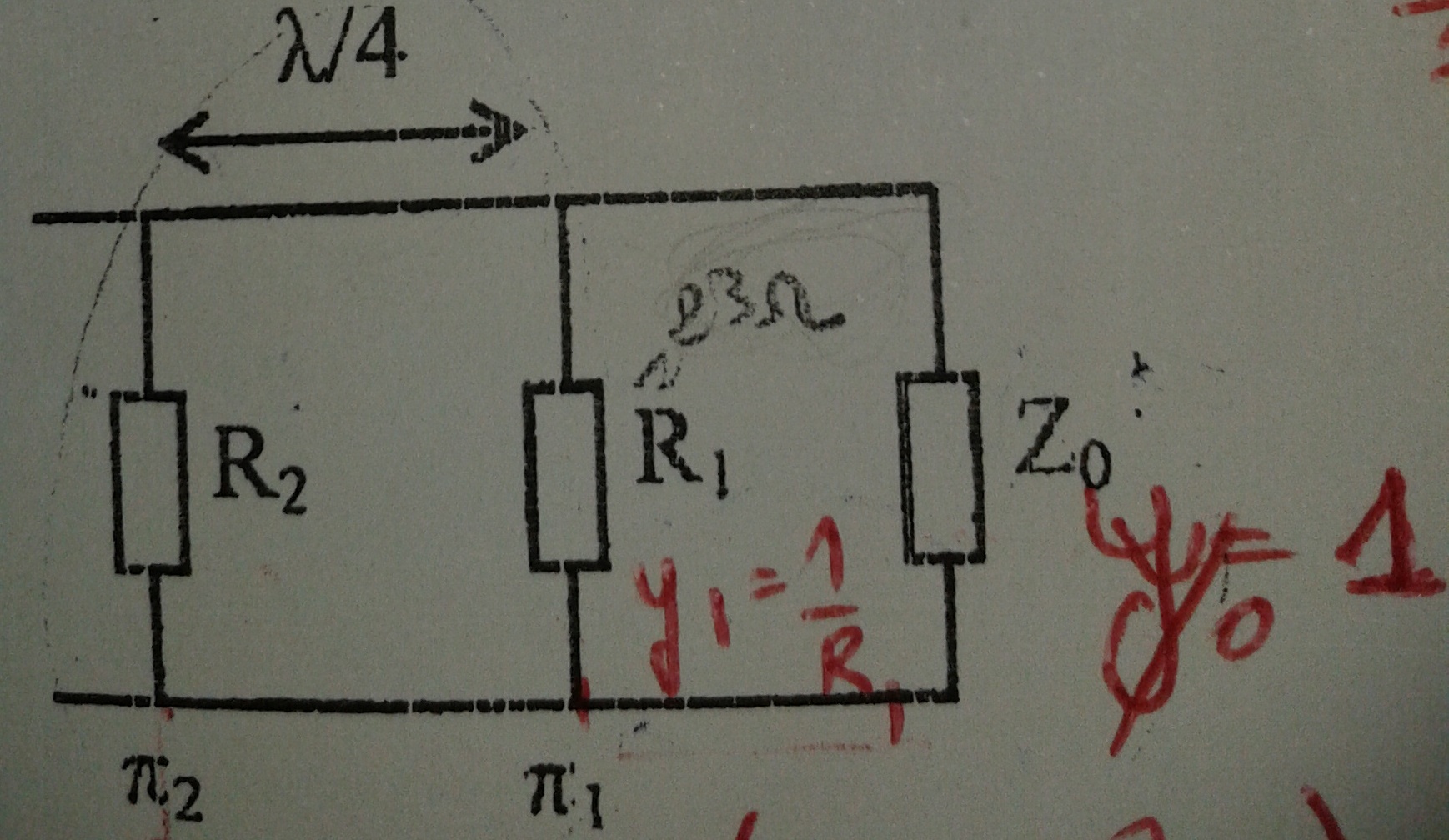
j'ai une ligne sans pertes d'impédance caractéristique Z0=50 ohm est terminée par une charge adaptée.On intercale deux résistance R1 et R2 en
parallèle et distantes de λ/4 , comme le montre la figure ci-contre .
je veux déterminer l'admittance réduite au plan π2 (pi 2).
une idée SVP . Merci
please ???? help me !!
Bonjour.
Soit vous travaillez avec l'abaque de Smith, soit vous utilisez la formule de l'impédance ramenée. C'est à dire, l'impédance vue à l'entée de la ligne, dans votre cas.
Vous trouverez la formule dans le web. Par exemple dans ce site:
http://michel.hubin.pagesperso-orang...chap_prop3.htm
Dans votre cas, vous aurez un problème car la tangente deest infinie pour un quart d'onde.
Mais si vous regardez à quoi tend la formule quand
Au revoir.
D’après ce que je sais , l'admittance au plan ( pi 1) y1= (1+(1/R1)) ( car y0=1 : charge adaptée) , donc au plan (pi 2) sa devra être y2= y1 +(1/R2) ; je croix que j'oublie quelque chose parce que j'ai pas utilisée la distance λ/4 entre le plan 1 et 2 . Alors si vous pouvez m'aidez ?? et sinon je ne voix pas comment utilisée la formule ( si Bl tend vers pi/2 alors tangente de Bl tend vers l'infini ) alors que dois-je comprendre ??
P.S : j'ai essayé de travaillé avec la formule mais je n'arrive pas à trouvé la réponse ??
Re.
Savez-vous calculer la limite d'une expression ?
Si vous ne le savez pas, faites-le "à la calculette".
Prenez les valeurs numériques et calculez le résultat pour la tangente égale à 1000, puis 10000, puis 1 000 000, etc. Vous aurez le droit de vous arrêter un peu avant l'infini. Mettons pour tan(Bl) = 1090.
A+
mais bien sur que je sais calculer la limite d'une expression ; c'est pourquoi je t'avais dit, si j'utilise la formule B=2 pi / λ , X la distance est égale λ/4 , alors j'aurais lim (tang de pi/2 ) = infini et puis j'utilise la formule générale de l'impédance d'entrée pour avoir mon admittance au plan (pi 2) ?? la ou je me beuge ???
Re.
Que donne la formule de l'impédance ramenée pour lambda ?
Écrivez la formule résultante que vous obtenez. Car j'ai l'impression que vous n'avez pas compris ce que je vous ai dit de faire.
A+
mais c'est ce que je n'arrive pas à trouver ??? la formule générale est Ze= Z0 × (Zl +jZ0tgBl)/(Zo+jZl tgBl) . De plus on a lim (tang de pi/2 ) = infini à la distance X=λ/4 ( quand je ramène Z0 au plan 1 , j'aurais Z0 parallèle à 1/R1 ce qui nous donne l'admittance réduite y1 =(1+ ( Z0/R1) ) ) maintnant je doit ramené ce qui est dans le plan 1 au plan 2 ou il y a 1/R2 , mais je n'arrive pas à le faire ??
Re.
Dernière tentative et après j'abandonne:
Que donne cette formule:
Ze= Z0 × (Zl +jZ0tgBl)/(Zo+jZl tgBl)
quand tgBl tend vers infini ?
A+
Ze=( Z0 * Z0) / Zl
Re.
Finalement !
C'est tout. Vous n'avez qu'à l'utiliser.
A+
looooool; mais je connais cette réponse dés le début mais comment l'utilisée ?? c'est ça ma question est ce que je met Zl= R1 ou bien Zl= 1/(1+(Z0/R1))+ 1/R2
Re.
ZL est l'impédance qui charge l'extrémité de la ligne. Dans votre cas c'est Zo en parallèle avec R1.
alors yl ( réduite) = (1+ (Z0/R1)) puisque y0=1 ????? c'est ça !!!
Zl =( R1 Z0 / (R1+Z0) ) par suite Ze =( Z0 ( R1+Z0)) / R1 et l'impédance réduite ze= (R1+Z0) /R1 , alors ye= R1/ (R1+ Z0) .
j’espère que c'est juste cette fois si ????
please answer me
Un conseil : sans forcément retenir la formule Gamma(L) = Gamma.exp(-2j.beta.L) pour le coefficient de réflexion d'un tronçon de longueur L, tu pourras gagner du temps en connaissant quelques cas intéressants :
-> si L est multiple de la demi-longueur d'onde, rotation de k tours dans l'abaque de Smith donc Gamma(L) = Gamma
-> si L est un multiple impair du quart de longueur d'onde (L = (2k+1)pi/Beta), Gamma(L) = -Gamma soit z' = 1/z ou encore Z' = Rc²/Z. C'est le cas dans ton exo : un tronçon de longueur lambda / 4 s'appelle un transformateur quart d'onde et se comporte comme un inverseur d'impédance.
-> si le tronçon de ligne est chargé par un court circuit (Z = 0), Gamma = -1 donc le tronçon court-circuité se comporte comme une réactance pure : Z(L) = jRc.tan(beta.L), positive (capacitive) ou négative (inductive) selon que L est plus petit ou plus grand que lambda/4. On peut donc réaliser n'importe quelle réactance avec un tronçon de ligne court-circuité.
-> si au contraire l'impédance de charge est infinie (circuit ouvert) on obtient Z(L) = -jRc.cotan(beta.L), idem on peut réaliser n'importe quelle réactance.
C'est important en pratique puisque c'est entre autres avec ça qu'on se débrouille pour réaliser l'adaptation de n'importe quel récepteur ou émetteur...
Et oui pour ton exo, l'admittance totale vaut 1/R2 + 1/Zl, et pour Zl on s'embête pas on reconnaît l'inverseur quart-d'onde : Zl = Z0² / Zeq avec Zeq = R1//Z0.
d’après ce que vous m'avez dit si je fais le calcul je trouve que l'admittance réduite total est égale à ye= Z0/R2 + R1/(R1+Z0) , normalement c'est la réponse juste n'est ce pas ??
Pour moi oui. Mais je peux me tromperC'est si important que ça (DM noté ?), au point que vous ne fassiez pas confiance à vos compétences en calcul ?...
hhhhhhhhhhhhhhhhhhhh, on faite dés le début j'avais le même résultat que vous , donc si vous le confirmé je suis sur que la réponse est correcte maintenant
thank youuuuuuu
juste une dernière autre confirmation : si je dois calculer R2 pour qu'il ait une adaptation au plan 2 sachant que j'ai la valeur de R1 , donc il suffit de mettre ye=1 n'est ce pas ?? puisque on veut une adaptation ???
( et c'est juste une révision pour mon examen )
Oui, si ze = ye = 1, le coefficient de réflexion est nul, i.e toute la puissance est transmise.
ouiiii, merci beaucoup
