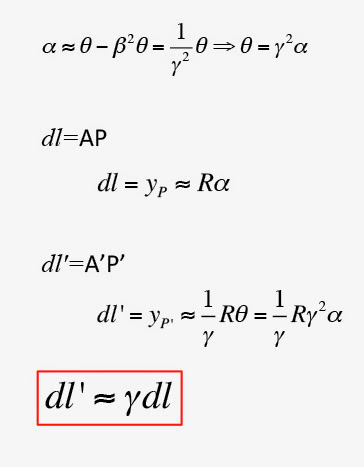Bonjour,
J’ai toujours été intrigué par les résultats qui découlent de l’étude d’un disque en rotation relativiste : la circonférence propre augmente mais pas le rayon ce qui pousse à abandonner la géométrie euclidienne. Une autre conséquence gênante est l’impossibilité de synchroniser les horloges sur la circonférence et l’apparition d’une déchirure temporelle (time gap).
Ces résultats bizarroïdes découlent de l’approximation initiale suivante :
« un arc de la circonférence du disque est considéré pendant un petit moment comme un référentiel inertiel »
Or, cette hypothèse me semble fausse : on ne peut pas assimiler un arc de circonférence à un référentiel inertiel.
Pour être plus précis, en notant R le référentiel inertiel dans lequel tourne le disque :
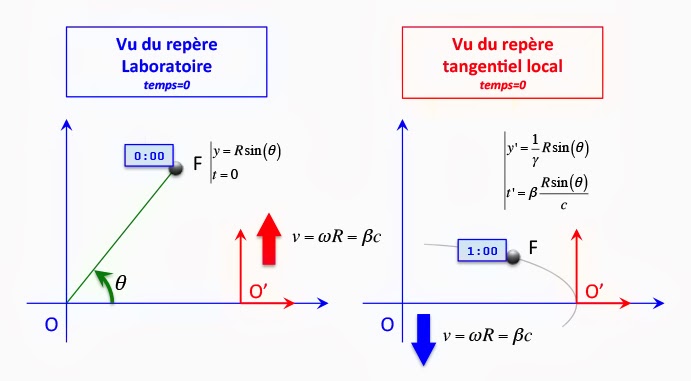
- Je peux considérer un référentiel inertiel local L
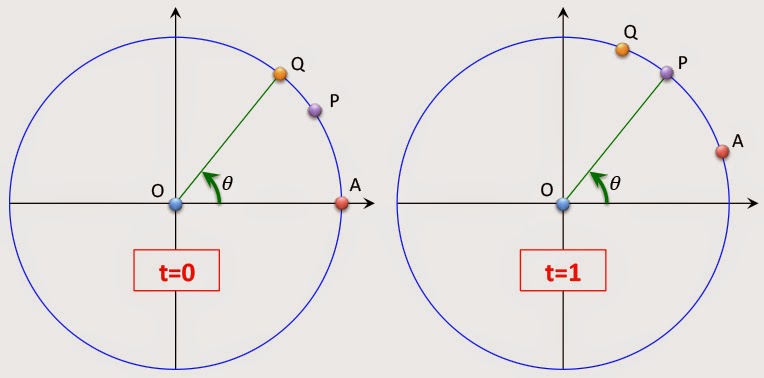
- Pendant un petit laps de temps, l’arc de circonférence sera immobile par rapport à L
- MAIS il y a une déformation relativiste entre l’arc et le référentiel L
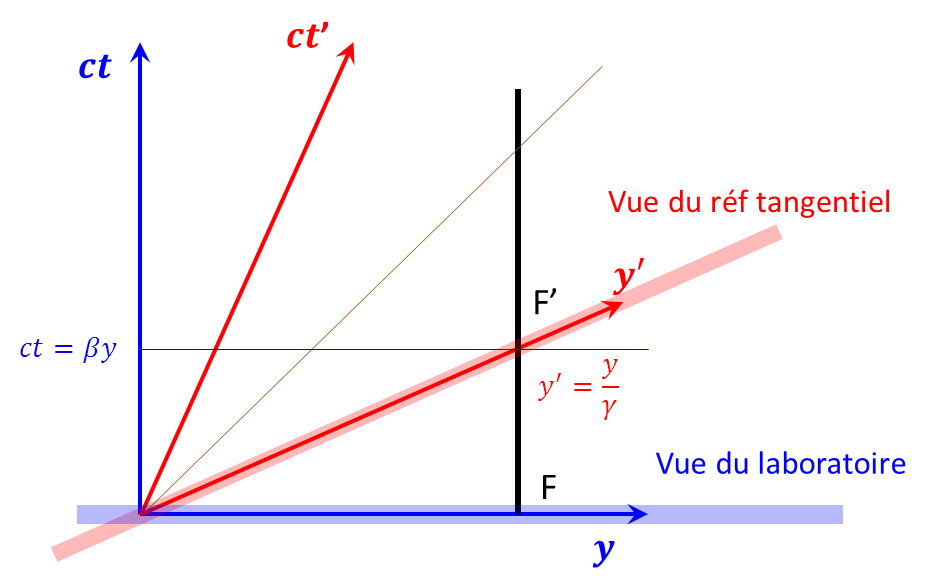
- Cette déformation est une dilation (L voit l’arc de cercle dilaté) d’un facteur gamma
- Comme vues de R les longueurs du référentiel L sont contractées d’un facteur gamma : le référentiel R mesure la longueur propre de l’arc de circonférence
Finalement les choses sont très simples : le disque en rotation reste dans la géométrie euclidienne et les horloges sont synchronisées sur les cercles concentriques.
J’ai documenté cette analyse ici.
-----