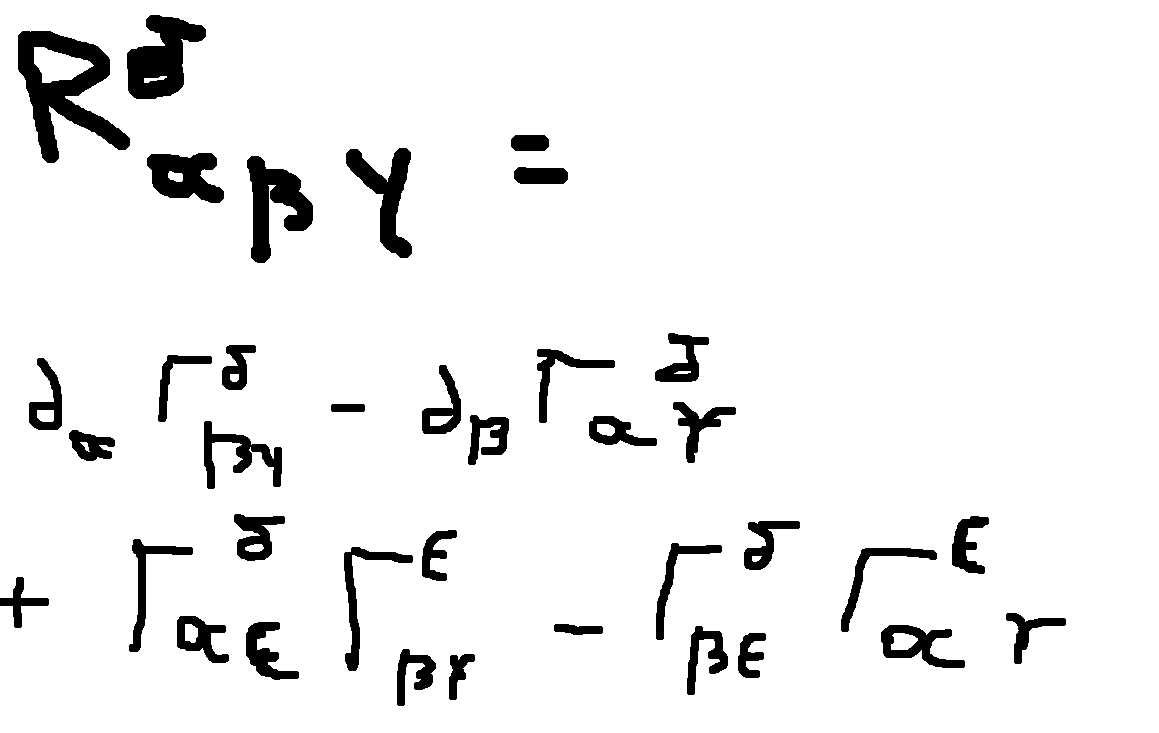Bonjour, soit V une variété différentielle, en chaque point M il existe un système de coordonnées locale (x⁰, x¹, x², x³). Je demande juste
juste au lecteur(s) de confirmer ou non, s'il(s) lui(leurs) plaît(plaisent), mes dires.
Définir un champ de vecteur sur une variété consiste à associer à chaque point M de coordonnées locale (x⁰, x¹, x², x³) un vecteur de l'espace tangent. En d'autres termes, on définie 4 fonction de (x⁰, x¹, x², x³) noté fp ou p va de 0 à 3 et en posant (∂0; ∂1; ∂2; ∂3) une base de l'espace tangent, le vecteur u de l'espace tangent associé au point M est noté(j'utilise la convention d'Einstein.). :
u = fp(x⁰, x¹, x², x³)∂p
Merci d'avance et bonne fin d'après midi.
-----



 .
.
 .
. ?
?

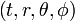 dans la variété de dimension 4 correspondant à l'espace temps n'est ce pas?
dans la variété de dimension 4 correspondant à l'espace temps n'est ce pas?





 merci pour la réponse, donc mes Va sont des fonctions de M et plus précisément de
merci pour la réponse, donc mes Va sont des fonctions de M et plus précisément de  Merci de me répondre bonne soirée.
Merci de me répondre bonne soirée.
 .
.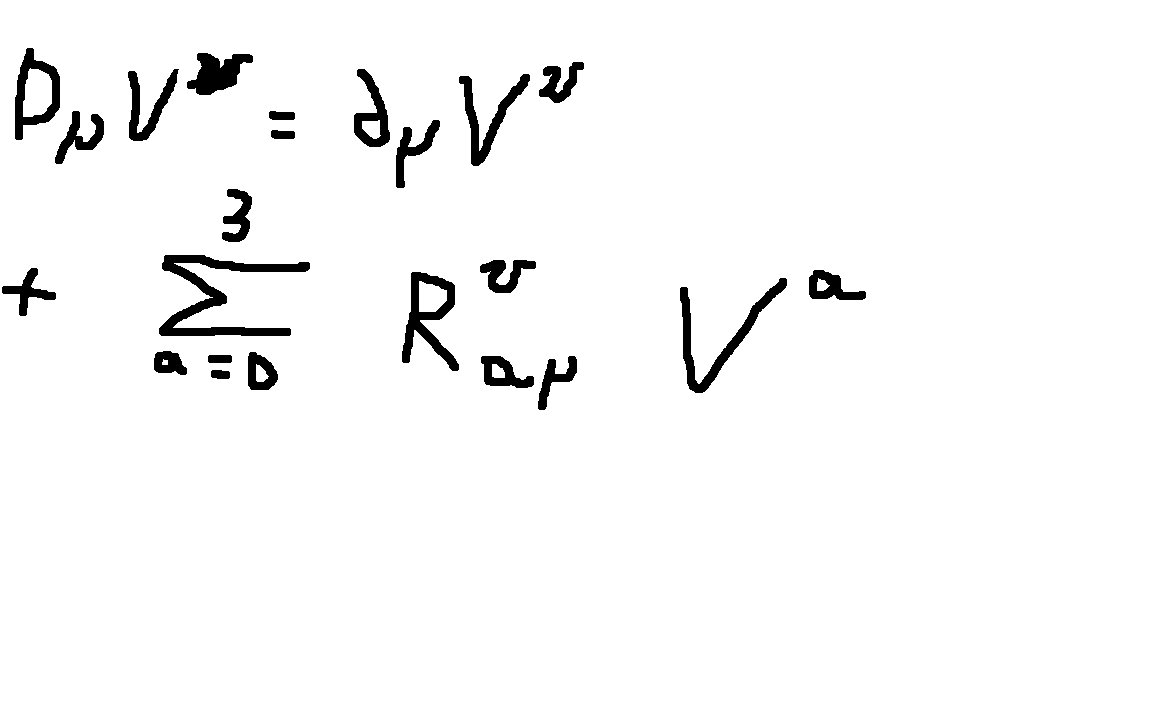 ?
?