dérivée partielle seconde (pour les ondes)

[Minialoe67]

Bonjour!

Premier cours d'ondes de l'année et 1ers soucis!
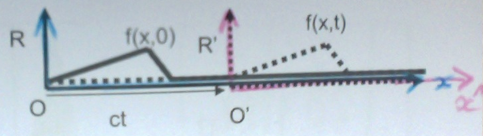
Soit une onde progressive croissante (définit par x (espace) et t (temps)) et la perturbation f (f(x,t)).
on a f(x-ct) (c=célérité). On pose a=x-ct

df/dt = -c df/da (là je suis d'accord)
d²f/dt² = -c * d²f/da² * (-c)= c² * d²f/da². (là je suis perdue, expliquez moi svp ce qui a été fait)

Mais on sait que df/dx=df/da (je suis ok) et d²f/dx²=d²f/da² (perdue là aussi!)

Pouvez vous me donner le calcul entier pour que je puisse comprendre les parties en rouge? je pense que mon problème est surtout un problème mathématique dû aux dérivées secondes...
Merci de m'aider
-----

[LPFR]

Bonjour.
On ne pose pas une équation d'onde dans l'abstrait. Mais uniquement d'un système physique bien déterminé.
À partir d'une fonction quelconque f(x-ct) vous ne pouvez pas déduire que df/dt = -c df/da.
Imaginez que la fonction 'f()' soit le logarithme népérien.

Je vous suggère de lire ce premier chapitre sur des ondes (dans ce cas sur une corde). Il vous donnera de basses un peu plus physiques:
http://forums.futura-sciences.com/at...n-ondes2-a.pdf
Au revoir.

[coussin]

À partir d'une fonction quelconque f(x-ct) vous ne pouvez pas déduire que df/dt = -c df/da.
Imaginez que la fonction 'f()' soit le logarithme népérien.

Bah si, non ?
Y a que da/dx entre les deux. La fonction f est quelconque, même le logarithmique népérien.

[Amanuensis]

Perso je trouve que les notations devraient être plus rigoureuses, en distinguant la fonction à deux variables de la fonction à une variable ; on note .

La première égalité se lit , puisque .

La différentielle seconde est , en appliquant exactement le même principe qu'utilisé pour obtenir la première égalité.

[A voir en vidéo sur Futura]

[LPFR]

Bah si, non ?
Y a que da/dx entre les deux. La fonction f est quelconque, même le logarithmique népérien.

Re.
Oui. Vous avez raison. Au temps pour moi.
A+

[Minialoe67]

On ne pose pas une équation d'onde dans l'abstrait. Mais uniquement d'un système physique bien déterminé.

Je reprend du début alors:
Soit une perturbation f fonction de l'espace et du temps f(x,t)
on considère une onde progressive (x croissant)
Si on suit la perturbation dans le référentiel mobile R', f ne dépend que de l'abscisse f(x')
on a alors x=x' +ct ou x'=x-ct
=> f ne dépend que de la variable x-ct : f(x-ct) (on pose a=x-ct).

[Minialoe67]

Amanuensis, je pense avoir compris vos explications.

Par contre d²f/dx²=d²f/da² me pose toujours problème...
Avec vos notations d²ø/dx²= d/dx ((x,t) => f'(x-ct)) =f"(x-ct) j'ai essayé ça. C'est juste?

[LPFR]

Je reprend du début alors:
Soit une perturbation f fonction de l'espace et du temps f(x,t)
on considère une onde progressive (x croissant)
Si on suit la perturbation dans le référentiel mobile R', f ne dépend que de l'abscisse f(x')
on a alors x=x' +ct ou x'=x-ct
=> f ne dépend que de la variable x-ct : f(x-ct) (on pose a=x-ct).

Pièce jointe 228131

Re.
C'est bien ce que je dis. C'est un exercice de mathématiques. Pas de physique.
A+

[albanxiii]

Bonjour,

Je propose de passer par les dérivées de fonctions composées.

On pose et alors on a .

On sait alors que car .

Et ensuite je vous laisser finir.... sachant que bien sur , vous êtes d'accord ?

Le principe est le même avec les dérivées par rapport au temps, en tenant compte du fait que qui est une simple constante.

@+

[Amanuensis]

Ce qui avait déjà été expliqué plus tôt... Doit y avoir une raison à la répétition?

[Amanuensis]

Par contre d²f/dx²=d²f/da² me pose toujours problème...

Quelque chose m'échappe: si vous voyez pourquoi (avec vos notations) df/dt = -c df/da, alors les trois autres cas (dérivée seconde par rapport à t, dérivée première par rapport à x et dérivée seconde par rapport à x) s'obtiennent exactement de la même manière.

Je vous suggère de reprendre la démo de "df/dt = -c df/da", de bien la comprendre, et de l'appliquer aux trois autres cas.