Roulement sans glissement

[lora2000]

Bonjour,
alors je ne comprends pas bien la condition de roulement sans glissement .. j'ai des difficultés à résoudre cet exercice



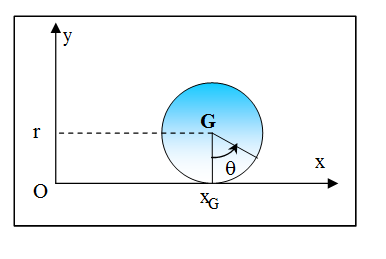
Soit un solide (S) constitué d’un disque de centre G, de rayon r, en contact sur un plan xOz le long de l’axe Ox.
Le mouvement est étudié dans le référentiel lié au support R = (O, x,y,z).
On note xG l’abscisse de G suivant Ox et (téta) l’angle représentant la rotation du disque.
* Montrer que dans le cas du roulement sans glissement, on obtient ( dx_G)/dt=-r (d(téta))/dt


je sais que R.S.G implique que v(s₁/s₂)=v_2/0-v_1/0 = 0
et v_1/0 est égal à 0 puisque I₁ est fixe du sol
mais je sait pas comment calculer v_2/0
j'ai essayé de faire v_2/0=v_(G,s2/R)+ rotation de s2/R vectoriel GI
mais je sais pas à quoi est égal v_(G,s2/R)
vraiment je suis perdu

-----

[LPFR]

Bonjour.
Au lieu d'aligner de tas des formules et des vecteurs, j'enroulerais une bande de papier sur le pourtour du disque, qui se collerait sur le support en bas.
Il suffit alors de calculer la longueur de bande qui est transférée au bout d'un temps quelconque.
Au revoir.

[lora2000]

je vous remercie infiniment pour votre réponse mais malheureusement je suis obligée de travailler avec la formule V_G = V_2/0-V_1/0 puisque c'est un exercice d'application de cours

[obi76]

Bonjour,

à mon avis vous raisonnez à l'envers. Vous avez une formule et vous essayer de voir où la mettre pour que ça marche. Ce n'est pas du tout la bonne méthode.

Comme vous l'a dit LPFR, un peu de logique et de l'imagination vous permettra déjà de dénouer la situation. La formule de cours ensuite interviendra naturellement pour répondre aux problèmes que vous aurez lors de la résolution.

[A voir en vidéo sur Futura]

[lora2000]

Merci obi76 pour votre réponse .... j'ai déjà essayer de travailler avec la méthode de LPFER mais j'ai rien trouver :/ + je crois que cette methode est indépendante de la relation que j'ai déjà donné .. vraiment je suis perdue xp le problème est avec v(G,s2/R) faut juste savoir comment le calculer et puis mon problème sera résolu

[obi76]

Lorsque le rouleau fait un tour (donc theta va de 0 à 2 pi), G va de où à où ?

[lora2000]

va de O à XG c'est à dire il tient la distance XG

[obi76]

Alors déjà deux choses :

- faites bien attention à voir dans quel sens va theta. Quand theta augmente, G il va vers la droite ou vers la gauche ?
- lorsque le rouleau fait un tour, on est d'accord que le centre du rouleau parcours une distance égale à sa circonférence (ce qui revient à dire ce qu'avait évoqué LPFR) ?

[lora2000]

alors dans ce cas il va vers la gauche puisque le sens de theta est vers la gauche .. aussi je comprend parfaitement que G parcours la distance égal a la circonférence de reouleau

[obi76]

donc on est d'accord :

(on va l'appeler comme ça)
,

ou mieux :

Jusque là, vous avez des questions ? (il faut absolumet que vous comprenniez TOUT ce que je viens d'écrire...).

[lora2000]

ok je crois que c'est clair et j'ai aucune question pour l'instant

[obi76]

vous croyez ou c'est sur ? Vous sauriez le refaire ?

Si oui, prenez ce que j'ai écrit, et dérivez à droite et à gauche par le temps. Qu'obtenez vous ?

[lora2000]

je suis sur ....d'ou on peut conclure que dXG/dt=dx₀/dt-r.d (théta)/dt
et puisque x0=cst alors dx0/dt=0 n'est ce pas ?
( on peut remarquer que V_2/0=dx₀/dt et V_1/0=r.d(theta)/dt )

[obi76]

je suis sur ....d'ou on peut conclure que dXG/dt=dx₀/dt-r.d (théta)/dt
et puisque x0=cst alors dx0/dt=0 n'est ce pas ?

Exactement, donc vous avez répondu à la question, même pas besoin de la formule que vous vouliez absolument utiliser... Après, ce que sont v2/0 et v1/0, je ne sais pas ce que c'est donc je ne peux pas vous dire....

[lora2000]

ok merciii bcp

[obi76]

De rien