Oui c 'est exacte, c'est ce qui te pose un probleme.Et pour être franc j'avoue que la frontiére physique/ mathématiques peut être floue dans certains cas. Dans ces cas il faut adopter une convention pour que tout le monde se comprenne.Envoyé par stefjm
J'y travaille et j'aimerais bien arriver à des définitions claires.
Le gars qui modélise la moduilation (entre autres) en utilisant plein de fréquences négatives : Il ne fait pas de la physique?
Que penses-tu de la modulation QAM?
Que penses-tu de mon moteur quantique?
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Bonsoir,
Dsl, j'ai pas tout lu ^^'.
Mon frère m'avait donné des pistes très claires pour me représenter les séries de Fourier et les transformées :
C'est très simple dans le cas des séries, en se plaçant dans le plan complexe on voit facilement que l'histogramme des coefficients de Fourier correspond à la longueur des exponentielles iwkt tournantes(aiguilles) à une fréquence fk...du coté négatif du spectre, on a celles tournant dans le sens horaire, et du côté positif, celles tournant dans le sens trigo. On met ces aiguilles bout à bout (somme). On a une espèce de système bielle manivelle évoluant dans ce plan complexe, et en bout de système on retrouve la fonction périodique. Dans le cas d'un coefficient de Fourier complexe... la longueur de l'aiguille est donnée par le module du coeff, et l’argument du coeff donne le déphasage de cette aiguille par rapport aux autres.
Pour les transformées de Fourier, c'est un peu la même chose sauf que le spectre au lieu d'être discret est continu. Du coup des aiguilles, il y en a une infinité et elles sont infiniment petites sauf si on a des distribution de Dirac dans le spectre. Mais sinon le signe indique toujours le sens de rotation de ces aiguilles.
Est-ce que ça aide ?
En espérant avoir pas dit trop de bêtises.
Au revoir
Dernière modification par interferences ; 28/04/2014 à 18h48.
Ce n'est pas le doute qui rend fou, c'est la certitude.
Dans le cas d'un dirac, l'aiguille est toujours infiniment fine (pas d'épaisseur) mais sa longueur est infinie. Ce qui est fini est son poids, ie son aire, produit de sa longueur par son épaisseur, qui vautpour un
J'espère que cela aide.
Vous avez décrit une représentation physique de quelque chose.
J'appelle cela faire de la physique et d'autres appelle cela faire des maths. (et je ne suis pas tout seul heureusement!)
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Non non.
Dans le cas d'un Dirac, la longueur de l'aiguille est finie...mais elle est pas infiniment petites comme les autres. Il n'y a pas de notion d'épaisseur.
Mais rien qu'avec une infinité dénombrable d'aiguille de longueur finie (Somme) on ne peut décrire que des fonctions périodiques (Série de Fourier).
En revanche quand on passe à la transformé de Fourier dans le cas général on a une infinité non dénombrable d'aiguille de longueur infiniment petite (Intégrale).
Si par hasard on a besoin d'une aiguille de longueur finie (composante périodique de la fonction) ben on utilise la notion bien utile de distribution de Dirac.
Ci-dessous la représentation des aiguilles de sinus et cosinus avec leur sens de rotation quand on parcours x dans le sens croissant :
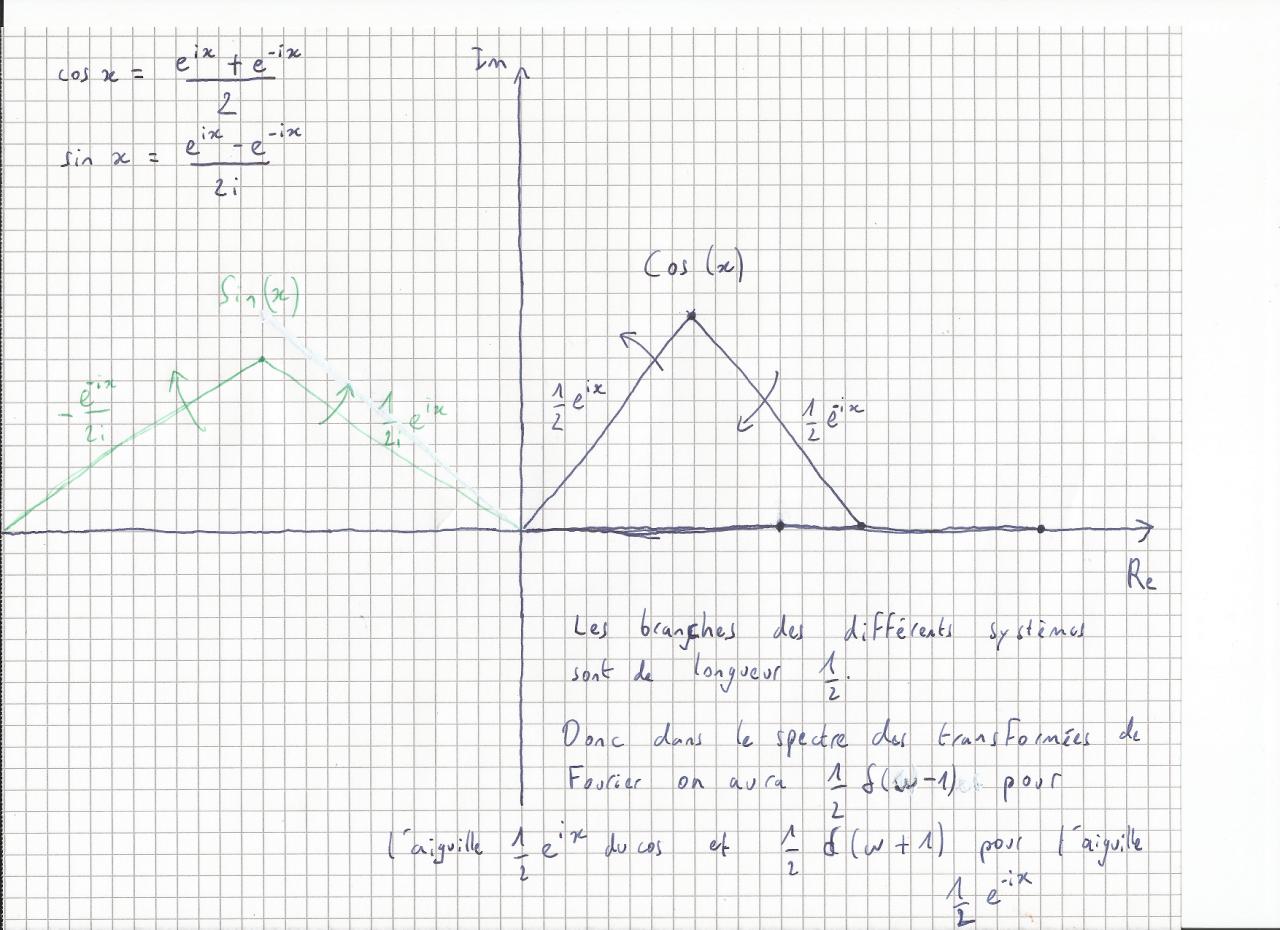
On comprend très bien dans ce cas que la notion de fréquence négative est stupide et que le signe n'indique que le sens de rotation des exponentielles.
Dernière modification par interferences ; 29/04/2014 à 10h12.
Ce n'est pas le doute qui rend fou, c'est la certitude.
PS : Désolé si un mathématicien passe par là ^^'
Ce n'est pas le doute qui rend fou, c'est la certitude.
Bonjour stefjm
à mon sens ce n'est pas qu'une question de sémantique, moi j'appelle ça enseigner la physique par le biais des maths.
Je ne cherche pas à te convaincre, j'ai mieux à faire, mais dis-moi comment tu prouves par les maths que "c" est une vitesse limite pour la matière par exemple. Avec les maths rien n'empêche de trouver une vitesse infinie, avec l'expérience on retombe sur terre.
Voilà, pour moi un physicien fait des expériences et ensuite utilise les maths pour (r)enseigner celui qui veut bien se pencher sur le problème.
Un prof peut se contenter de la seconde partie.
L'electronique, c'est fantastique.
Exact.
Je n'avais pas compris que tu étais resté coté temporel avec les aiguilles.
Ta représentation montre bien pourquoi un moteur asynchrone monophasé ne peut pas choisir tout seul son sens de rotation. (Tes aiguilles sont une représentation de son rotor, un moteur spatialise le sinus électrique.)
Mais je ne dis rien de plus depuis le début.
En quoi le sens de rotation d'exponentiel ne serait-il pas physique?
On peut trouver des tonnes d'exemples qui le mette en évidence.
Pourquoi?
Cela ne me semble pas faux.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Je ne comprends pas le lien entre ta remarque et le sujet de ce fil.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Re,
On peut même imaginer une transformation qui donnerait uniquement des coefficients réels à des fréquences situées dans le plan complexe.
On aurait alors des "fréquences complexes" où le signe de la partie réelle donne le sens de rotation et l'argument la phase.
Du coup on pourrait lire le spectre de la transformées sous forme de surface apparaissant sur le plan complexe
Au revoir
Dernière modification par interferences ; 29/04/2014 à 11h54.
Ce n'est pas le doute qui rend fou, c'est la certitude.
PS : En fait il faut 2 surfaces dans le plan complexe sinon on a pas assez de déphasage (seulement pi pour les positif et les négatifs).
Ce n'est pas le doute qui rend fou, c'est la certitude.
Il faudra que réfléchisse à cette représentation. Tu t'en es déjà servi?On peut même imaginer une transformation qui donnerait uniquement des coefficients réels à des fréquences situées dans le plan complexe.
On aurait alors des "fréquences complexes" où le signe de la partie réelle donne le sens de rotation et l'argument la phase.
Du coup on pourrait lire le spectre de la transformées sous forme de surface apparaissant sur le plan complexe
En considérant la variable directement complexe,
ca se fait déjà en transformée de Laplace où la variable de Laplace est complexe.
Sa partie réelle représente l'amortissement (positif ou négatif) et la partie imaginaire la fréquence.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Re,
Non, non je ne m'en suis pas servi.
Mais après ça reste toujours des transformées de Fourier.
C'est juste que la représentation du spectre est différente.
Ce n'est pas le doute qui rend fou, c'est la certitude.
Après, j'ai réfléchi un peu, c'est mieux de prendre un plan complexe pour les fréquences complexes des aiguilles tournant dans le sens horaire et un autre plan complexe pour les fréquences complexes des aiguilles tournant dans le sens trigo.
On a alors dans le cas des séries de Fourier, une série de la forme :
Avec :
On observe donc :
Ce n'est pas le doute qui rend fou, c'est la certitude.
Après, j'ai réfléchi un peu, c'est mieux de prendre un plan complexe pour les fréquences complexes des aiguilles tournant dans le sens horaire et un autre plan complexe pour les fréquences complexes des aiguilles tournant dans le sens trigo.
On a alors dans le cas des séries de Fourier, une série de la forme :
Avec :
On observe donc :
Et pour wk>0 :
Pour wk<0 :
PS : Si quelqu'un pouvait supprimer le doublon ^^'...merci d'avance
Dernière modification par interferences ; 29/04/2014 à 21h37.
Ce n'est pas le doute qui rend fou, c'est la certitude.
PPS : Sinon pour wk=0 :
Ce n'est pas le doute qui rend fou, c'est la certitude.
Bonjour,
J'ai l'impression qu'il y a une ambiguïté générale entre ce qui tourne et ce qui ne tourne pas.
La confusion n'est pas facile à éviter en raison des habitudes à passer en complexe les grandeurs réelles sans pour autant passer dans l'espace réciproque. (Je ne sais pas si c'est très clair?)
Je le constate en général, y compris pour moi, pas pour interférence en particulier.
Exemple :
Un cosinus
Une exponentielle imaginaire
Si je reprends mes moteurs asynchrones, il est clair qu'un cosinus vibre, mais ne tourne pas.
Pour que cela tourne, il faut un déphasage,
1) soit deux bobines à -90° alimentées déphasées à -90° (donc cosinus, sinus), racine carré de l'unité négative
2) soit trois bobine à -120° et -240° alimentées déphasées (donc triphasé), racine cubique de l'unité
Les représentation 1) et 2) sont équivalentes tant d'un point de vu maths, que d'un point de vue physique. Dans les deux cas, il y a création d'un champs magnétique tournant.
Par contre, une seule bobine ne crée pas de champ tournant, mais un champ pulsant, ie, deux champs tournants en sens inverse l'un de l'autre.
0) Une seule bobine crée un champ pulsant.
Plutôt que de parler en terme de champs tournant, on peut parler en terme d'onde :
Dans les cas 1 et 2, on a une onde progressive qui se propage dans l'entrefer et tourne en rond.
Dans le cas 0, on a une onde stationnaire, somme de deux ondes progressives.
Merci à interférence pour ses aiguilles qui illustrent très bien le fonctionnement des moteurs.
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Bonjour,
Hé bé...
Je fais un four avec un bête moteur asynchrone monophasé en physique?
Bon, un peu d'optique et de TF déniché par Phuphus.
http://www.tsi.telecom-paristech.fr/.../TF2Dimage.htm
Images à fréquences pures
Comment un physicien "non négatif" interprête-t-il les trois points? (continu, +f, -f)
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Je t'avoue que je ne comprends pas trop pourquoi 3 points et pas 2, mais sinon, comme n'importe qui qui sait que la TF de 1 est un delta de dirac, et qui sait que sin w= (e^iw-e(-iw))/2i,(tu la vois dans le deuxième terme la "fréquence négative"????????) je ne comprends vraiment pas ce que tu ne comprends pas.
Parce que le spectre de Fourier est symétrique.
ben oui!
et la TF d'un sinus est deux delta symétriques.
Qu'un physicien puisse dire qu'une pulsation négative est moins physique qu'une pulsasion positive...
Un automaticien utilise couramment des pulsations p complexes en Laplace.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
c'est vraiment un dialogue de sourd. parlons de représentation si tu veux. Si on représente une EXPONENTIELLE complexe quelconque, une représentation commune et complète est celle du plan complexe. Dans ce cadre e^(-iw) est juste le conjugué de e^(iw) ok? Jusqu'ici c'est tout à fait facile de se le représenter, maintenant si on a e^(-iwt), et qu'on cherche une représentation de ça dans le plan complexe, alors il s'agit d'une exponentielle complexe qui tourne (donc qui évolue dans le temps) dans le sens inverse de e^(iwt), je vois mal comment avoir une interprétation au delà de ça. On pourrait bien dire que e^(-iwt)= e^(iw(-t)), mais alors il serait IMPOSSIBLE d'en avoir une représentation dans le temps. Donc à ce moment là, nous faisons quand même un peu d'interprétation physique puisque nous utilisons la seule évolution du temps qui fasse sens pour nous (c'est à dire vers les t croissants). Maintenant concernant un sinus, ou un cosinus, la fréquence DU SINUS et non pas des exponentielles, (car les delta sont les delta centrées sur les fréquences des exponentielles) n'a qu'une seule interprétation, c'est le nombre de battements par seconde (enfin tout dépend des unités), qu'on pourrait associer à n'importe quelle amplitude d'une fonction périodique (sinusoidale). Donc je répète, quel est le problème la dedans?????
si
a=u+v
b=u-v
alors
u=a/2+b/2
v=a/2-b/2
Pour pouvoir interpréter, il faut déjà fixer à l'avance de quoi on parle, une exponentielle complexe, ça n'a pas vraiment d'interprétation en dehors du plan complexe. Un sinus n'a pas de représentation dans le plan complexe (à par la projection de l'exponentielle sur un axe), mais en a une très "intuitive" à interpréter dans le plan réel: on associe la hauteur à une amplitude.
PS: il me semblait que ça donnait delta(w-pi/2)+delta(-w-pi/2), donc seulement 2 pics.
Bonjour,
C'est déjà pas mal non?
Cela montre qu'un sinus ou un cosinus tourne dans les deux sens et pas dans un seul choisi arbitrairement.
Cela se voit très bien quand on regarde le champ tournant créé par une seule bobine : deux champs qui tournent en sens inverse.
https://www.youtube.com/watch?v=OyfyrjzyeH8
Je cite http://fr.wikipedia.org/wiki/Maurice...nc_(ingénieur)
«Le théorème de Leblanc énonce qu'une bobine alimentée par une tension alternative et créant de ce fait un champ magnétique pulsant le long de son axe créé en fait deux champs magnétiques, de même module, tournant en sens inverses. Ce théorème constitue la base théorique du fonctionnement des moteurs asynchrones monophasés.»
Je trouve que c'est une très belle représentation physique, à l'aide d'un champ magnétique qui permet de représenter le plan complexe.
Une autre belle preuve physique est qu'un moteur asynchrone monophasé ne démarre pas tout seul, car il ne peut pas choisir son sens de rotation!
S'il a déjà un sens de rotation, il continue sur sa lancée. Une des fréquences est privilégiée. A vide, le moteur tourne à f en suivant f. (glissement f-f nul). Le champ à L'autre fréquence -f devient négligeable car il tourne à -2f par rapport au rotor.
Je remplace Chaverondier un moment pour rappeler qu'on peut envisager une évolution à rebrousse temps.
Oui pour les fréquences définies comme réelles positives.
Non pour celles issues de transformée de Fourier (réelle positive et négative) et pour celle issues de transformée de Laplace (complexe).
Je ne comprends pas pourquoi le statut «physique» est accordé aux premières et pas aux secondes...
Cela en a plein...Il suffit de demander aux mathématiciens...
Par exemple,
1) les matrices de rotation dont a parlé gatsu au début de ce fil.
2) les vecteur de Fresnel
3) le fait qu'une multiplication par
4) le fait qu'une multiplication par
Plus toutes celles que j'oublie...
Et alors?
Je ne conteste pas cette interprétation physique.
Je me demande simplement pourquoi les autres interprétations physiques que je propose sont rejetées par certains physiciens comme n'étant que mathématique. (et pô physique...)
Je cherche juste à comprendre ce rejet... et à savoir s'il est légitime et en particulier par quels arguments il est justifié.
Jusqu'à présent, je continue à enseigner comme physique toutes les interprétations que j'ai données dans ce fil, car les arguments des physiciens définis positifs ne m'ont pas convaincu.
Oui pour un sinus (ou cosinus) sans composante continue.
Dans le cas de l'image, on a du mal à définir plus «blanc que blanc» et il y a donc une valeur moyenne non nulle d'où la raie à fréquence nulle.
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Bonsoir,
Je vois que mon petit exemple de visualisation par un champ tournant physique (un champ magnétique, c'est bien physique?) n'a pas inspiré grand monde...
Je trouve cela curieux...
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
bonsoir Stefjm , j'ai regardé la vidéo , j'ai vu
, on revient au point de départ.
Dernière modification par azizovsky ; 12/05/2014 à 20h23.
Il me semble, qu'au message #383; nous pouvons tordre le coup à cette question ambigu sur est-ce physique / ou non, car ce qui importe dans toute modélisation c'est son aspect prédictif "réfutable" par expérimentation. Cela nous le savons depuis belle lurette me semble t-il sans invoquer une quelconque ontologie non (de manière consciente ou pas) ?
Patrick
Dernière modification par invite6754323456711 ; 12/05/2014 à 20h32.
salut ,j'ai oublié un
désolésalut ,j'ai oublié un
Bonsoir,
Admettre les fréquences négatives, c'est admettre les périodes négatives, donc les "distances temporelles" négatives.
Remarquons que si la longueur d'un objet ne saurait être que positive, une distance peut être négative. De même:
alors que la durée d'un événement ne peut être que positive, on peut concevoir beaucoup plus facilement une "distance temporelle" négative.
Et je crois que c'est ce qu'on fait en analyse spectrale : on calcule ce que ça donne si on imagine qu'on revient en arrière dans le temps.
Mais, alors qu'on peut réellement déplacer dans l'espace dans les deux sens de l'axe, on ne déplace réellement sur l'axe du temps que dans le sens positif.
Ou alors ce serait remettre en question un des aspects les plus basiques de la science physique (comme B. Chaverondier semble prêt à le faire) !
La réalité, c'est ce qui reste quand on cesse de croire à la matrice logicielle.
je suis fatigué :
Ou difficultés entre mathématique et physique. En mathématique il est possible de construire une distance pour ensuite pouvoir parler de cercle
Et ne pas être perturbé par un résultat exprimé dans un cadre formel donné. Poincaré parlait de pluralisme théorique.A circle is a set of points with a fixed distance, called the radius, from a point called the center.
Patrick
