Bonjour à tous.
Voici mon problème:
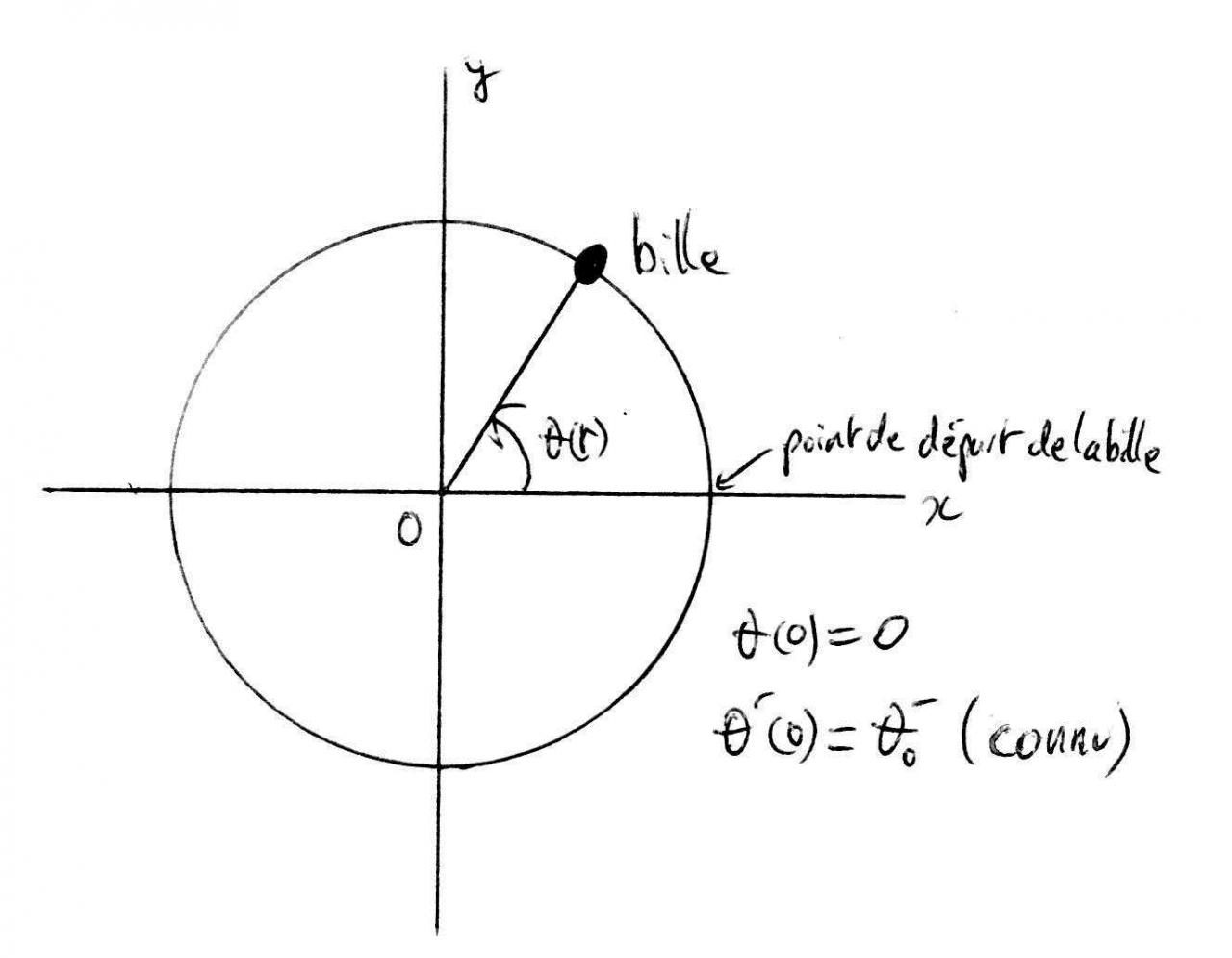
une bille tourne le long d'un cercle de rayon R (par exemple dans un rail circulaire).
On lui donne une vitesse angulaire initiale theta0. J'aimerais obtenir l'angle theta(t) (angle entre l'axe centre du cercle-bille et l'axe des abscisses) en fonction du temps t sachant qu'il y a des frottements.
Le but, c'est de dessiner dans un logiciel une roulette de casino avec une bille qui tourne dedans, en tenant compte des frottements.
Merci.
Bonjour et bienveu au forum.
Les frottements d'une bille qui roule sont des frottements de roulement (inconnus pour la version française).
Ne pas confondre avec les frottements "ordinaires" (de glissement).
Mais je vous souhaite bon courage pour trouver le coefficient de frottement de la bille de la roulette (en ivoire ou en plastique ?) contre le rail (bois ? acier ? plastique ?).
Une fois calculée la force de frottement, l'énergie cinétique (de translation et de rotation) diminue du fait du travail de la force de frottement. Ce qui permet de calculer la vitesse de la bille et sa position.
Au revoir.
Bonjour et merci pour ta réponse.
Ma modélisation n'a pas à être très proche de la réalité.
Je pensais simplement supposer que la force de frottement est proportionnelle à la vitesse (mais ça ne marche pas dans le cas d'une bille?). Pour le coefficient, je prendrais ce qui m'arrange pour l'animation à l'écran.
Ce qui m'intéresse, c'est le reste: les détails pour obtenir theta(t). J'aimerais avoir le raisonnement.
Merci.
Re.
Je ne vois pas qui sont thêta0 ni thêta.
Pouvez-vous faire un petit schéma ?
A+
Je me suis trompé: je voulais dire thetaprime0 (vitesse angulaire initiale) au lieu de theta0.
Voici le schéma:
Merci bien de m'expliquer en détail comment obtenir theta(t).
Re.
Aux vitesses des billes de roulette, la force de freinage aérodynamique est négligeable.
Donc, on peut considérer qu'elle est constante, ce qui donne une accélération angulaire 'alpha' constante et négative.
Vous n'avez qu'à essayer pour trouver celle qui vous donne un effet visuel acceptable.
Les formules sont les mêmes que pour le mouvement uniformément accéléré, en changeant les distances par des angles, les vitesses par des vitesses angulaires et les accélérations par des accélérations angulaires.
A+
Merci pour votre réponse. Ça devrait convenir.
Oui, mais dans ton modèle je crois que ta « force » de resistance est prop à la vitesse.
Donc le alpha n’est pas constant.
Je raisonnerai donc plutôt en vitesse avec
et
avec
À intégrer pour avoir
Bonjour Anset.
Qu'est qui vous fait penser qu'aux vitesses des billes de roulette ce soit le frottement aérodynamique qui soit prépondérant ?
Au revoir.
ce n'est pas moi,
c'est ce que j'ai compris de SON modèle tel qu'il l'a présenté dans ses messages.
il ne parle pas d'aérodynamisme mais de force ( frein ) prop à la vitesse
mais peut être ai je mal saisi !
donc je n'ai pas d'interprétation personnelle, je traduit "bêtement".
Re.
Son modèle est mauvais.
Comme le lui ai dit. Aux vitesses de la bille, ce sont des frottements de roulement qui sont prépondérants. Et c'est la solution que je lui ai proposé.
A+
pas de soucis,
lu un peu trop vite l'intro de ton mess #6, ( et forum physique ici, pas math !)
cordialement.
Rebonjour.
Est-ce que vous pouvez valider mon raisonnement pour être sûr que c'est bien ça:
Dans l'article
http://en.wikipedia.org/wiki/Rolling_resistance
ils disent que la force de frottement de roulement est F=Crr N où Crr est une constante et N est la force normale à la surface.
Je suppose qu'on peut considérer que N est constante, donc la force de frottement est constante (en négligeant la force de frottement avec l'air).
Et là, j'aimerais avoir des précisions pour justifier que la dérivée seconde de theta est constante (on utilise la formule m a=somme des forces? dans quel repère?)
Merci.
Bonjour.
On travaille toujours dans le repère de la table de la roulette que l'on considère comme inertiel.
Mais je viens de m'apercevoir que comme la force de frottement roulant dépend de N (la normale) et que cette normale est surtout donnée par la force centripète. Et que cette force centripète est proportionnelle à
Donc, contrairement à ce que j'ai dit, l'accélération angulaire n'est pas constante mais dépend du carré de la vitesse.
Mea culpa.
Le calcul de thêta est un peu plus compliqué. Un peu comme celui de Ansset au post #8.
J'obtiens:
Avec les 'b' et 'r' utilisés dans la page de Wikipedia.
Mais je ne suis pas sur de ne m'être pas trompé dans les calculs. Il serait bien si Ansset pouvait les faire indépendamment.
Au revoir.
Si la force de frottement est constante ( comme le précise LPFR ), alors il suffit de se réferrer à son post 6 pour voir l’équation de theta.
Polynôme du second degré, avec donc une décélération constante égale à 2*alpha.
Si la force de frottement est constante ( comme le précise LPFR ), alors il suffit de se reprendre son post 6 pour voir l’équation de théta.
Polynôme du second degré, avec donc une accélération (dérivée seconde ) constante égale à 2*alpha. ( alpha < 0 )
cordialement.
correction :
nos message se sont croisés.
Effectivement, pour une vitesse de bille de roulette la force centripète n’est pas négligeable, et le N ( force de contact a revètement ) ne peut se résumer au poids.
si on veut modéliser, (je l'écris en vitesse , pas en angle )
l'accélération vaut
on abouti à une équation diff non triviale !
en début de mouvement, on peut certainement négliger g, mais au fur et à mesure du ralentissement, la composante verticale prend de l’importance jusqu’à devenir principale à la fin !!
Bonjour Ansset.
Vous êtes bien plus courageux que moi. Car je n'ai pas tenu compte du poids dans la force sur le guide.
J'essaie de comparer à mon calcul avec g = 0, et je suis gêné par le t² de la formule de l'accélération. Je ne vois pas d’où il sort. Serait-il une erreur de copier-coller ?
Cordialement,
oui, oui, une erreur ce CC, et réécrivant en Latex ( le t² est oublier )
désolé
Re.Envoyé par ansset
Quand la vitesse est trop petite, la bille tombe du rail sur la partie tournante de la roulette (le cylindre, je crois).
A+
Annset, le N(t)/m=sqrt(g^2+v^4/R^2), tu l'as trouvé où , car je ne l'ai pas vu dans la page wikipedia?
Sinon, à part les forces de frottement, il y a d'autres forces qui s'appliquent, non, puisque la bille roule sur un rail circulaire? Il faut les prendre en compte?
Re.
Ansset a fait un dessin (d'ou moins dans sa tête) avec la force centrifuge et le poids et a utilisé le théorème de Pythagore pour trouver la normale.
Et non les seules forces qui accélèrent la bille sont des forces dirigées dans le sens d'avancement de la bille.
A+
Re.
Quand on regarde l'intégrale de la formule avec 'g':
http://www.wolframalpha.com/input/?i=int+dx%2Fsqrt%281+%2B+a*x^4 %29
on est vite convaincu qu'on peut (doit) négliger 'g'
A+
Oui, enfin tout dépend du rail !
Mais on peut effectivement négliger g pour toute une grande partie de mouvement.
Ex : R=1 ( grande roulette )
V=2T/s ou 3T/s au début par exemple
V²/R env 40 ou 100 et g 10.
De toute façon on peut le faire avec g=0….pour voir.
Donc finalement, je prends
et je remplace
S'il n'y a pas de solution simple pour cette équa diff, je peux essayer une résolution numérique (Euler, Runge-Kutta..) puisque c'est fait sur ordinateur.
Par contre, vous pourriez me faire une figure pour expliquer le
j'obtient simplement dans ce cas.
V(t)=1/(1/V0+(k/R)t)
ca v'=-(k/R)v²
Re.... (je sais, là j'abuse)
Oui. Vous abusez.
A+
Heu, un dessin non,
Même pas de logiciel pour ça !
Pythagore t’a bien expliqué LPFR
g vertical et V²/R ou Rw² comme tu veux à l’horizontal ( centripète )
Je reviens avec mes questions:
dans l'article wikipedia, ils disent:
et avant il est écrit:
"W is the load on the wheel in lbs."
Donc pourquoi avoir compté la force centripète dans N?
Bonjour,
Dans quel article de wiki ?
S’agit-il d’un objet en mouvement rotatif ou d’objet sur une trajectoire rectiligne ?
Je suppose sinon que le r est le rayon de la bille ou boule .
