Bonjour, mon lagrangien a pour expression:
L= 1/2M(x'2+y'2+z'2)+e(Axx'+Ayy'+Azz')-ePhi(r,t)
A(r,t) etant un potentiel vecteur
Phi(r,t) étant le potentiel scalaire
Si je calcul la formule d'Euler Lagrange pour la composante x à partir de la formule (d/dt)dL/dx'-dL/dx=0 j'obtiens d'apres le corrigé de mon prof:
Pourquoi les composantes Ay et Az sont elles dérivée par rapport à x? Dans mon calculs je n'ai pris en compte que la composante Ax.
-----




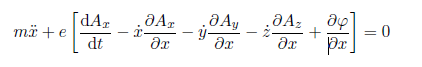

 est un champ vectoriel. En d'autre terme, c'est une fonction qui a chaque point de l'espace associe un vecteur. Et donc, chacun de ses composantes sont des fonctions de l'espace.
est un champ vectoriel. En d'autre terme, c'est une fonction qui a chaque point de l'espace associe un vecteur. Et donc, chacun de ses composantes sont des fonctions de l'espace.