Bonjour,
Je reprends ma question avec un seul disque. Cela suffit amplement pour comprendre mon problème. Ce n'est plus un problème de calcul car je trouve bien une énergie constante. C'est un problème de changement de variables, en mathématiques c'est correct mais cela me semble faux en physique.
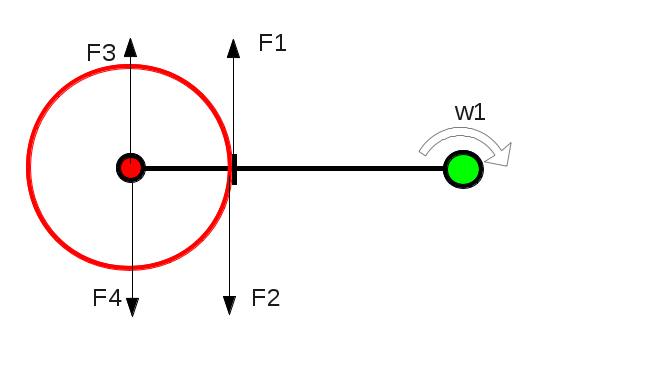
Le bras noir tourne à la vitesse angulaire de w1 dans le sens horaire. L'axe vert est fixé au sol. Le disque tourne à la vitesse w2 avec w2 < w1, le disque tourne donc sur lui même dans le sens trigo. Les vitesses w1 et w2 sont dans le référentiel labo. Je note w2' la vitesse de rotation du disque dans le référentiel bras. w2'=w2-w1 si je respecte le signe positif comme étant le sens horaire. w2' < 0. Il y a de la friction entre le disque et le bras ce qui donne les forces F1 et F2. Je choisis par exemple w1=10 et w2=2, donc w2'=-8.
Je considère le cycle suivant:
1/ Il n'y a pas de friction entre le disque et le bras. Je lance le bras à w1 et le disque à w2, ceci avec l'aide d'un moteur externe.
2/ Je retire le moteur externe.
3/ La friction entre les disques est mise en action de telle manière à fournir une force F constante même si la vitesse du disque change. Il n'y a pas d'autre friction ailleurs.
4/ Je mesure la somme de toutes les énergies, chaleur incluse, la somme doit être constante.
------------------------------------------------Le bras----------------------------------------------------
la vitesse angulaire évolue comme:
car le couple F1/F4 est dans le sens trigo
la différence d'énergie cinétique est donc de :

------------------------------------------------Le disque-------------------------------------------------
la vitesse angulaire évolue comme:
car le couple est dans le sens horaire
donc la différence d'énergie cinétique est:
------------------------------------------------La friction--------------------------------------------------
La friction donne une énergie de :
La différence d'énergie est bien nulle. Mais pour moi, l'intégrale devrait être:
La différence d'énergie devrait être de :
Au départ il y a w1 et w2, cela donne w2'=w2-w1 (w2' c'est w2 dans le référentiel bras). Il y a de la friction entre le disque selon la vitesse de rotation w2' et non selon w2.
Questions:
1/ Sans friction, si je modifie w1 à la main, est ce que w2' change ? Pour moi c'est non, c'est w2 qui change et qui dépend de w2' et de w1. En fait, la formule n'est pas w2'=w2-w1 mais w2=w1+w2'. Il y a une cause et une conséquence car la friction change w2' et w1 et par voie de conséquence w2. Donc je dois bien intégrer avec w2' du départ ensuite c'est uniquement la variation de la vitesse de rotation locale qui doit intervenir et non la variation de w1.
2/ Si je modifie w2' à la main, est ce que w1 change ? Pour moi c'est encore non, par contre w2 change.
Voilà, je voudrai comprendre pourquoi l'intégrale de la friction prendrai en compte l'évolution de w1.
Merci par avance de votre aide
A+
-----