Chute d'un corps dans l'eau, vitesse à l'asymptote

[inviteb9f49292]

Bonjour à tous,

J'ai un problème assez simple de chute d'un corps dans l'eau, mais le résultat de mon calcul est très éloigné de ce que j'observe, je voudrais donc soumettre mon raisonnement et l'application numérique à la sagacité du forum, pour qu'on me pointe où est mon erreur.

Je commence donc par poser le PFD:

où Mb est la masse de l'objet totalement immergé, dont j'ai séparé le volume en deux partie, Vb tel que


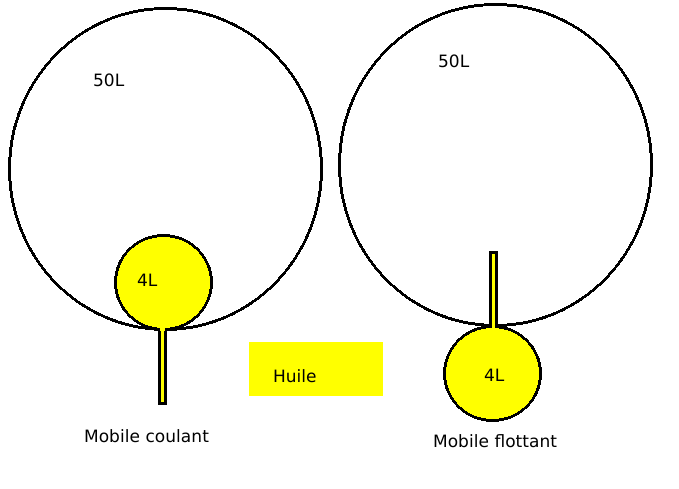
Bon but est de connaitre la vitesse asymptotique (lorsque l'accélération est nulle) pour un dV donné. Mon raisonnement est le suivant: au début nous sommes immobile (dV = 0), puis on gonfle (dV > 0) ou on dégonfle (dV < 0) l'objet, il va monter (v < 0, z pointe vers le bas) respectivement descendre (v > 0), lorsque la vitesse asymptotique est atteinte j'ai donc


L'objet est sphérique et d'expérience les vitesses max sont de l'ordre de 10cm/s, si c'est un écoulement laminaire, j'ai la relation

où mu est la viscosité de l'eau, Rb le rayon de l'objet et v sa vitesse en m/s, et l'application numérique me donne (rho = 1e3kg/m^3, mu = 1e-3 Pa.s, Rb = 0.5m) un transfer d'1m^3 corresponds à une vitesse de 1m/s, or le flotteur a un volume d'une 50aine de liltres, et on peut transférer 4L max ! Donc en gros j'ai un facteur 1000 à 10000 entre mon résultat théorique et ce que j'observe en réalité!

Ai-je fait une erreur de raisonnement ? ou peut-être une bête erreur de calcul (ma vitesse est mesurée en cm/s et mes transferts d'huile en mL, et je me suis plusieurs fois emmélé les pinceaux...) ?
Si le résultat est bon, cela est-il un argument fort pour justifier que nous serions en écoulement turbulent, ou bien ça n'a rien à voir ?

D'avance merci à tout élément de réponse.
-----

[invitecaafce96]

bonjour,
Il me semble bien reconnaître tous les termes , force-poids , poussée d'Archimède et force de frottement proportionnelle à la vitesse de forme -kv .
Donc, posée de façon habituelle, vous arrivez à une équation différentielle du premier ordre : my' + ky = Constante , pas très difficile à résoudre .

[inviteb9f49292]

vous arrivez à une équation différentielle du premier ordre : my' + ky = Constante , pas très difficile à résoudre.

Après une 10aine d'années quasi-exclusivement dédiée au dev informatique je suis un peu rouillé...

Si je trouve la fonction qui résouds mon équa. diff., penses-tu que sa limite puisse être différente de ce que j'ai tenté d'établir avec mon raisonement de base ?

J'ai appliqué le même raisonnement avec des frottements de Newton (proportionnels à la vitesse au carré), l'application numérique semble être bien plus proche de ce que j'observe. Du coup mon équa. diff. serait du type y' + ky^2 = cste, c'est solvable ce genre de bêstioles ?

[calculair]

Bonjour

Cette bestiole est solvable....

[A voir en vidéo sur Futura]

[invite6dffde4c]

Bonjour.
Le changement de volume n’est pas infiniment petit. Donc, évitez d’utiliser des différentiels qui faussent les formules.
Utilisez ΔV qui ne posera pas ces problèmes.

Je n’ai pas compris la manip. De quel transfert parlez-vous ?
Si Rb fait 0,5 m, son volume est nettement supérieur à 50 L, C’est plutôt 523 L.

Pour ce qui est de l’équation du mouvement, c’est une exponentielle.
Au revoir.

[inviteb9f49292]

Si je trouve la fonction qui résouds mon équa. diff., penses-tu que sa limite puisse être différente de ce que j'ai tenté d'établir avec mon raisonement de base ?

Equa. diff. résolue, la vitesse limite a bien la même expression que ce que j'avais déterminé avec mon raisonnement... Je suis donc cohérent mais ça ne colle toujours pas avec la réalité... Décidément la nature elle ni comprends rien en math !

Cette bestiole est solvable....

Cette bestiole a-t'elle un nom que je puisse soumettre à l'oracle google ?
Si tu as un début de piste a me refiler pour la résoudre je suis prenneur, parce que j'ai beau chercher dans mes vieux cours de sup/spé, je trouve pas grand chose pour cette forme...

[calculair]

Bonjour

Je ne suis pas au clair avec ton équation

le poids - archimède = F

le coefficient de frotement dans le fluide K

La vitesse V

l'equation de la dynamoque = M dV/dt = F - K V^2

M / ( F - K V^2 ) dV/dt = 1


On integre / au temps M / ( F - K V^2 ) dV = 1 dt


M tanh^-1 ( V racine K/F) / ( racine F K ) = t + cte


d'ou V = Racine ( F /K ) Tanh ( Racine (F K) ( t +cte )/ M )

La vitesse limite V = racine (F /K )

[inviteb9f49292]

Je n’ai pas compris la manip. De quel transfert parlez-vous ?
Si Rb fait 0,5 m, son volume est nettement supérieur à 50 L, C’est plutôt 523 L.

Il y en a au moins un qui suit! 0.5m c'est le diamètre de ma "presque" sphère, pas son rayon désolé. Malheureusement ça ne fait qu'un facteur 2... je suis loin de mon facteur 1000...
Par transfer il faut comprendre que j'augmente ou diminue le volume de mon mobile en transférant de l'huile entre une vessie extérieure souple et l'intérieur du mobile.

[inviteb9f49292]

M / ( F - K V^2 ) dV/dt = 1


On integre / au temps M / ( F - K V^2 ) dV = 1 dt


M tanh^-1 ( V racine K/F) / ( racine F K ) = t + cte


d'ou V = Racine ( F /K ) Tanh ( Racine (F K) ( t +cte )/ M )

La vitesse limite V = racine (F /K )

Super ! Merci ! Regarder ça plus en détail...

[invite6dffde4c]

Re.
Si c’est un volume, le facteur est 8 et non 2.
Je n’ai toujours pas compris la manip.
Pouvez-vous la décrire un peu plus clairement ?
De telle sorte qu’un arriéré comme moi puisse la comprendre ?
A+

[inviteb9f49292]

Si c’est un volume, le facteur est 8 et non 2.

Je parlais du facteur entre mon calcul et ce que j'observe, or le diamètre / rayon du mobile intervient dans le coeff de la force de frottement à la puissance 1.

Pouvez-vous la décrire un peu plus clairement ? De telle sorte qu’un arriéré comme moi puisse la comprendre ?

J'ai un mobile dont je veux contrôler l'immersion, pour celà je joue sur son volume (son poids étant constant) et donc sa densité, pour le faire couler ou remonter. Or j'aimerai prévoir la vitesse de mon mobile en fonction de sa variation en volume (que je contrôle). Et j'espère pouvoir également "inverser" cette relation, connaissant la vitesse du mobile, quel est la variation de volume que je dois appliquer pour pouvoir le stopper. J'espère que c'est plus clair.

Merci pour toutes les réponss

[calculair]

Bonjour,

Effectivement , je n'ai pas compris le détail de cette manip.

J'ai donné le calcul de la vitesse de chute pour un coprs indeformableet de masse fixe.

Il semble qu'i y ait des transferts de fluide dans la manip que je ne comprends pas.

Merci de nous préciser les choses et de valider peut être les réponses.

[invite6dffde4c]

Re.
Et il vient d’où, l’huile que vous injectez ? D’un réservoir externe ?
Car la densité de ce réservoir externe va changer elle aussi.
Sont-ils reliés par un tuyau ?
A+

[inviteb9f49292]

Nouvelle tentative d'explication:

Mon mobile est une sphère rigide reliée à une vessie déformable pour pouvoir échanger de l'huile dans les deux sens (sphère <-> vessie). Son volume est donc compris entre le volume de la sphère 50L (vessie totalement dégonflée), et 50L + 4L de vessie totalement gonflée. Comme le poids de l'ensemble est une constante (54kg environ), je maîtrise la flotabilité du mobile en transférant de l'huile, vessie totalement gonflée, densité du flotteur de 1000kg/m^3 le flotteur monte jusqu'à la surface (on travaille en eau salée où la densité est toujours supérieure à 1000). En rentrant de l'huile de la vessie extérieure vers la sphère, je diminue le volume -> j'augmente la densité -> le mobile plonge jusqu'à une couche d'eau de densité égale à celle du mobile.

C'est plus clair ? Besoin de plus de précisions ?

[invite6dffde4c]

Re.
Oui. Celle que je vous ai demandée. Si la vessie est solidaire avec la chose, le volume total restera constant et la poussée d’Archimède aussi. Ce que vous gagnez en flottabilité sur la chose, vous le perdez dans la vessie. Il faut une « vessie » à volume constant, comme dans les sous-marins.
A+

[calculair]

Bonjour,
Ce que j'ai compris

On a un mobile aquatique constitué d'une sphère riride de 50 L relié à une vessie dont le volume est controlé de V° à V° + 4 L

La flotabilité est controlé par le volume de la vessie. ( cette dernière est liée a la sphère par un lien fixeet fait partie du mobile )

Maintenant reste à savoir si la variaton de volume de la vessie modifie le coefficient de trainée du mobile.

[inviteb9f49292]

Oui. Celle que je vous ai demandée. Si la vessie est solidaire avec la chose, le volume total restera constant et la poussée d’Archimède aussi. Ce que vous gagnez en flottabilité sur la chose, vous le perdez dans la vessie. Il faut une « vessie » à volume constant, comme dans les sous-marins.

Les sous-marins utilisent des ballasts : le volume du sous-marin est constant, il se rempli d'eau -> augmente son poids -> augmente sa densité -> il plonge...

Dans mon, cas la vessie est bien solidaire de ma sphère, et l'ensemble sphère + vessie constitue le mobile. Lorsque la sphère aspire l'huile depuis la vessie extérieure (déformable), la vessie s'écrase, et le volume de mon mobile est diminué du volume d'huile aspiré. Le poids total du mobile reste identique, la vessie extérieure est plus légère de la quantité d'huile aspirée, mais la sphère s'est alourdie de cette même quantité. J'ai donc diminué mon volume pour un poids constant -> j'ai augmenté la densité -> je coule.

Si ce n'est toujours pas clair, j'essaierai de faire un schéma.

[inviteb9f49292]

Ce que j'ai compris

On a un mobile aquatique constitué d'une sphère riride de 50 L relié à une vessie dont le volume est controlé de V° à V° + 4 L

La flotabilité est controlé par le volume de la vessie. ( cette dernière est liée a la sphère par un lien fixeet fait partie du mobile )

C'est ça à un détails près, la vessie peut avoir un volume compris entre 4L et 0, c'est la sphère qui fait 50L, et ainsi mon mobile a un volume compris entre 50 et 54L

Maintenant reste à savoir si la variaton de volume de la vessie modifie le coefficient de trainée du mobile.

Lorsque j'en serai à ce niveau de détails ! Mais en pratique je ne pense pas que ça change grand chose car:
- le flotteur a une forme torturé avec une coque protégeant la sphère, et un cylindre protégeant la vessie -> je pense donc le le Cx sera assez éloigné du 0.47 de la sphère
- les vitesses restent relativement lentes (autour de 5cm/s)

De toute façon, je voudrais déduire le Cx en mesurant la vitesse asymtotique, si je fait une mesure sur une ascension j'en déduit le Cx vessie gonflée, et en mesurant la vitesse en descente, j'aurais son Cx vessie dégonflée.

[calculair]

Bonjour,

Je pense que le système est bien décrit


Reste à savoir si le calul proposé donne des résultats cohérents avec l'expérience. Si tu es à 10 à 15% près c'est une réussite.... S'il y a un coefficient 10 ou plus avec l'expérience c'est qu'il y a un os à ronger pour modéliser ton engin.

[invite6dffde4c]

Les sous-marins utilisent des ballasts : le volume du sous-marin est constant, il se rempli d'eau -> augmente son poids -> augmente sa densité -> il plonge...

Dans mon, cas la vessie est bien solidaire de ma sphère, et l'ensemble sphère + vessie constitue le mobile. Lorsque la sphère aspire l'huile depuis la vessie extérieure (déformable), la vessie s'écrase, et le volume de mon mobile est diminué du volume d'huile aspiré. Le poids total du mobile reste identique, la vessie extérieure est plus légère de la quantité d'huile aspirée, mais la sphère s'est alourdie de cette même quantité. J'ai donc diminué mon volume pour un poids constant -> j'ai augmenté la densité -> je coule.

Si ce n'est toujours pas clair, j'essaierai de faire un schéma.

Re.
Oui. Faites un dessin. Car votre raisonnement est faux. Le volume total, le poids et la densité, restent constants.
A+

[calculair]

Bonjour LPFR,

LE poids reste constant

Mais le volume varie avec celle de la vessie

La sphere de rayon 0,5 m est indeformable, son volume est fixe, c'est ce que j'ai compris.

Pour une force de 1kg de déséquilibre entre le poids et archimède la vitesse est voisine de 6 cm/s

[inviteb9f49292]

Oui. Faites un dessin. Car votre raisonnement est faux. Le volume total, le poids et la densité, restent constants.

Mon raisonement n'est pas faux puisque mon mobile monte et descent pour de vrai (ceci n'est pas un exercice), mais mon explication ne doit toujours pas être super clair, place à l'art:

Sommes nous d'accord ?

[inviteb9f49292]

d'ou V = Racine ( F /K ) Tanh ( Racine (F K) ( t +cte )/ M )

La vitesse limite V = racine (F /K )

OK j'ai retrouvé le résultat de l'équa. diff. dans le cas turbulent, merci Calculair pour l'énôrme coup de pouce. En plus, le raisonnement de la vitesse limite que j'exposais au tout début donne la même expression pour la vitesse asymptotique.

Pour une force de 1kg de déséquilibre entre le poids et archimède la vitesse est voisine de 6 cm/s

Par contre je ne trouve pas la même chose que toi pour l'application numérique, je trouve plutôt 18cm/s pour un transfer d'1L (je crois que j'avais pris le Cx à 0.8 mais je ne l'ai pas noté).
Je vais refaire une passe.

[invite6dffde4c]

Re.
Bien, cette fois j’ai compris. Calculair avait, lui, bien compris. Le volume de 50 L est constant.
Par contre, je ne vois pas l’intérêt de la vessie externe. Il suffit de la vessie interne que l'on remplit avec l'eau de mer. Ce qui éviterait de que le Cx change.
A+

[calculair]

Bonjour, si je me souviens mon Cx est de 0,5

Par contre, il y aurait une correction a apporter s'il faut tenir compte de Rehnold..

Je pense qu'il faur d'abord valider la vitesse

V = racine (F / K )


Si f = 1 kg ou 10 N

K = 1/2 d S Cx = 0,5 x 1000 x 3,14 x0,5 x0,5 * 0,5 = 196

Racine 10 /196 = =0,22 m/s le crois que j'avais oublié de prendre la racine carré..

[inviteb9f49292]

Par contre, je ne vois pas l’intérêt de la vessie externe. Il suffit de la vessie interne que l'on remplit avec l'eau de mer. Ce qui éviterait de que le Cx change.

C'est un compromis "technologique", en vrac un circuit hydraulique qui resiste chimiquement à l'eau de mer c'est plus cher, un ballast nécessite de l'énergie pour le remplir et le vider (pompe), un design avec la vessie souple permet d'économiser l'énergie pour rapatrier l'huile à l'intérieur: on ouvre le robinet et on laisse la pression de l'eau écraser la vessie souple... Il y en a peut-être d'autre, je ne suis que l'informaticien de la troupe je n'ai pas participé à cette phase de la conception...

[calculair]

Bonjour

Par curiosité

1) les vitesses calculée sont elles cohérentes

2) a quoi sert ce super Ludion ? un drone maritime ?

[inviteb9f49292]

Racine 10 /196 = =0,22 m/s le crois que j'avais oublié de prendre la racine carré..

si je me souviens mon Cx est de 0,5

J'achète.

Par contre, il y aurait une correction a apporter s'il faut tenir compte de Rehnold..

Késakéou ? Parce que Mr Google n'a pas l'air de le connaître... E si c'est Reynolds, je ne vois pas la correction à laquelle tu penses.

[calculair]

Bonjour,


Le CX n'est pas constant, il dépend des dimensions, de la vitesse et de la viscosité du milieu.

Il faudrait un specialiste de la mecanique des fluides pour nous expliquer pourquoi cela varie. C'est lié à la viscosite du fluide.

[inviteb9f49292]

Le CX n'est pas constant, il dépend des dimensions, de la vitesse et de la viscosité du milieu.

OK si je reformule (histoire d'être sûr d'avoir compris), le Cx dépends de la vitesse (Reynolds), du coup l'équation doit être plus compliquée à résoudre...
Bah je te rassure, j'ai bien plus important pour compliquer l'équation différentielle: la densitée de l'eau dépends de la profondeur, à la louche la densité augmente de 5kg/m^3 tout les mètres. D'où une équa. diff. de la forme:

où la densité rho(z) est (dans un 1er temps) un pôlynome d'ordre 1.
Si tu sais comment ce type d'équa diff se résouds, je suis intéressé pour ma culture générale car je pense que le résultat n'est ni pertinent ni exploitable dans mon contexte.

Merci encore pour toutes ces lumières.