Bonjour à tous,
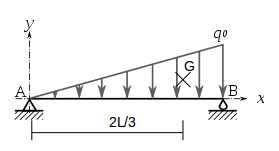
Pourriez-vous me donner des indices pour m'aider à démontrer qu'une charge linéique est équivalente à une charge appliquée au centre de gravité ? Il me semble avoir compris que le centre de gravité en question n'était pas celui de l'objet sur lequel était appliqué la charge mais le centre de gravité de la répartition de charge mais je ne suis pas sur. Du coup j'aimerais démontrer la formule pour comprendre tout les tenants et aboutissants.
D'avance merci.
Bonjour.
Ici, quand vous parlez d’équivalence il s’agit du couple produit par la charge.
Si cette charge est, le point d’application d’une seule force qui ferait le même effet (couple) se calcule de la même façon que le centre de gravité :
Au revoir.
Bonjour,
Merci de votre réponse. Auriez-vous des liens vers une démonstration de cette formule ?
Bonjour,
C'est la formule classique pour déterminer un baricentre (ou centre de gravité) => cf moyenne
En revanche, cette simplification n'est valable que pour les efforts externes à l'objet (PFS). Si tu veux rechercher les efforts internes (effort tranchant et moment fléchissant) cette simplification devient fausse
"Quand le calcul est en contradiction avec l'intuition, je refais le calcul"
Salut
Non , mais on peu la justifier .Envoyé par Shadowlugia
Je décortique un peu les éléments de langage pour clarifier :
_ "charge linéique" : répartissions de force sur une ligne , En quelque sorte une densité de force . Une densité de force peut être relative à une surface (forces de contact=pression) ou un volume (force à distance) . Elle est toujours de la forme λ(x,y,z)
_ "équivalente à" : Dire que deux charges sont équivalente (en dynamique) , revient à dire qu' elles ont la même résultante et le même moment en même un point .
_ "une force appliquée au centre de gravité" : C' est une force purement théorique , unique en ponctuelle dont le moment est nul au point G , donc équivalente à un ensemble de forces particulier (Dans le cas général cette équivalence n' est pas possible)
_centre de gravité de la répartition de charge : ????
Donc le problème se résume à :
_Déterminer le résultante (somme) des forces : le dénominateur de la formule de LPFR
S=∫λ(x,y,z).dl ou .ds ou .dv
_Déterminer le moment résultant en un point p : Mp=∫(λ(x,y,z)ΛR(x,y,z)).dl ou .ds ou .dv
_ Écrire que ce moment en p est égal à celui d' une force de même résultante et de moment nul en un point G soit : Mp = PGΛS
_Résoudre Mp = PGΛS en utilisant la « division vectorielle » . On constate que la solution n' est pas un point , mais une droite parallèle à la résultante . C' est l' axe de moment nul aussi appelé « droite d' action » voir même parfois « droite qui porte la force »
Quoi qu' il en soit la démarche est la même pour une répartissions de charge linéique ou surfacique ou volumique .
La formule ne me semble pas homogène. Si par exemple la densité de force est linéique, tu as les unité suivantes :Déterminer le moment résultant en un point p : Mp=∫(λ(x,y,z)ΛR(x,y,z)).dl ou .ds ou .dv
- lambda (x,y,z) en N.m-1
- R(x,y,z) en N
- dl en m
Le produit de l'ensemble te donne des N2
J'entends bien mais j'aimerais justement savoir pourquoi on peut réduire l'ensemble au centre de gravité du champs de force.C'est la formule classique pour déterminer un baricentre (ou centre de gravité) => cf moyenne
Pour illustrer ma demande, je vais prendre le cas suivant :
La force associée à la charge linéique est de la forme :
Je place le point G, centre de gravité du triangle formé par le champs de force
Le PFS appliqué à AB avec les moments en A donne :
D'où en changeant les points d'application des moments :
En prenant
Ceci est bien la formule que l'on doit trouver mais ce que j'aimerais comprendre, c'est pourquoi je peux considérer que ma force linéique possède un moment nul au centre de gravité du champs de force. Pourquoi ce n'est pas le centre de gravité de la poutre par exemple ?
Merci d'éclairer ma lanterne. Je butte sur ce problème depuis plusieurs jours et je n'arrive pas à trouver une démo me permettant de comprendre.
R comme Rayon : vecteur (ou bipoint) allant du point p au point de coordonnées x,y,z
Tu cherches une force (unique et ponctuelle) équivalente à ton champs de force , pas à ta poutre .
Bonjour,
Après avoir analysé vos réponses et notamment celle de Dynamix, je suis parvenu à la démonstration suivante :
Soit
- q(x) une densité de force quelconque
- F(x) la force associée à cette densité
- P un point quelconque
- Pour i variant de x=0 à x=L, Ai désigne le point d'application de F(x)
La somme des moments en P vaut :
Soit Feq la force équivalente à la densité de force q(x). On note G son point d'application. Deux forces sont égales si leur torseur en un même point sont égaux.
D'où :
La condition sur les moments donne :
Le point G d'application de la force équivalente est donc le barycentre des Ai associé aux poids FAi. Les coordonnées de G sont connues grâce au maths.
Pouvez-vous me valider cette démonstration ?
Bonjour.
Au moyen âge, on brûlait vivants les personnes qui écrivaient des intégrales sans différentiel.
Au revoir.
Haha, je pense qu'au Moyen Age ils auraient brûlé tout ceux utilisant des intégrales. En revanche aux Lumières (période d'introduction de la notion d'intégrale) nous ne pratiquions plus de telle pratique
Mis à part les différentiels manquants et les x sous-entendus, peux-tu me dire si cette démonstration comporte des erreurs ?
Re.
Désolé, vous équations sont trop compliqués pour moi.
Je ne vois pas l’utilité de travailler avec des vecteurs alors que toutes les forces ont la même direction.
Et tous les produits vectoriels sont entre vecteurs perpendiculaires.
Je n’aime pas déchiffrer des équations inutilement compliquées. Je ne suis pas maso.
A+
Les forces n'ont pas forcément la même direction étant donnée que la densité de force est quelconque.
Les produits vectoriels sont entre vecteurs perpendiculaire dans le cas d'une densité linéïque (c'était l'objet de ma demande initiale je vous l'accorde) mais sont laissé tel quel dans cette démonstration afin de permettre une généralisation à une charge volumique (il suffit d'introduire des intégrale triples).
J'ai préféré ne pas simplifier ces équations afin de pouvoir généraliser facilement cette démonstration. J'attendrais qu'un autre lecteur daigne la lire si vous ne le faites pas
Dans le cas quelconque , ta densité de force est un champs .
La résultante et le moment à l' origine sont des circulations sur la courbe formée par l' ensemble des points i .
Les éléments différentiels ne sont donc pas un luxe , ils sont indispensable .
Rétropédalage :
Ce n' est pas une circulation , mais ça y ressemble .
La différence , c' est que l' élément dl est un scalaire .
Bonjour,
Mais cette démonstration a déjà été faite. On s'en sert même tous les jours.
Si vous voulez vraiment le démontrer, je vous suggère de calculer le moment créé par la charge au centre de gravité (à 2L/3) et vous verrez que ça fait 0.
Donc vous aurez la démonsration pour ce cas de charge.
Vous pouvez également le faire pour un rectangle, un trapèze, un triangle centré sur la poutre, etc etc etc si vous voulez vraiment vous en convaincre.
C'est bien ed vouloir comprendre les choses mais là, je pense que vous perdez votre temps pour rien (mais c'est votre droit).
PS : vouloir généraliser à tout type de chargement c'est bien, sauf que dans la réalité, les chargements sont souvent des rectangles, triangles,trapèzes, paraboles mais rarement autre chose
"Quand le calcul est en contradiction avec l'intuition, je refais le calcul"
