Solution du problème à deux corps au repos

[harmoniciste]

Bonjour
@ 1max2
Universus à proposé UNE solution c'est à dire une intégrale générale de l'équation différentielle. Ainsi, il faut encore lui ajouter les bonnes "constantes" pour obtenir l'intégrale particulière qui correspondra aux conditions particulières à respecter.
Il y a donc des termes à ajouter pour respecter les conditions de l'instant t =0: position (31m) et vitesse (0 m/s)
De même que l'expression à accélération constante n'est pas x = 1/2 a t², mais x = 1/2 a t² + V₀ t + x₀

Le raisonnement de mach3 donnant la vitesse relative à toute distance r de séparation doit très certainement y être associée avec profit.
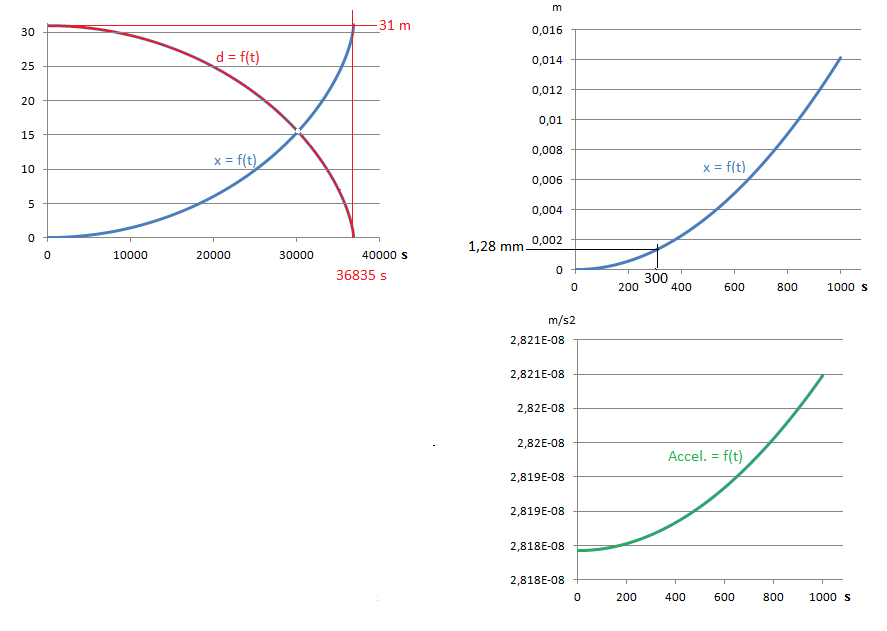
(Il me semble toutefois que cette vitesse est plutôt dr/dt = (2G.M.(1/r - 1/R⁰)^0,5 et non pas dr/dt = (4G.M.(1/r - 1/R⁰)^0,5) C'est en tout cas ce que donne ma simulation EXCEL, qui résoud très facilement ce problème de façon non analytique, en calculant l'accélération, la vitesse, la distance parcourue, par step de 10 secondes)

@dynamix
Bien sûr que la réalité (masses non-homogènes) complique encore le problème.
-----

[invite391b927d]

Ok, je commence à comprendre votre point de vue. Je vais réfléchir à tout ça.
Encore merci pour votre aide à tous.

[legyptien]

Je me trompe peut etre puisque personne ne l a proposer mais je crois qu a votre question je dirai:

r(t)=1/2 g(t) * t^2 + v1*t + r0 avec v1 la vitesse initiale. et g(t) l acceleration de la gravitation qui depend du temps evidemment puisque les 2 corps se rapprochent... cette fornule est vrai uniquement vrai avant collision r(t) superieur a la somme des rayons des 2 astres...

ok je viens de voir la reponse de Harmoniciste...

[1max2]

Bonjour , je me demandais, si ,en prenant 2 masses égales M et les lâchant sans vitesse initiale de la distance d l'équation ne dépendrait pas des masses .
Je m'explique, comme 2 objets de masse différente tombent à la même vitesse dans un champ de gravitation, on pourrait penser que 2 masses m plus petites, lâchées dans les même conditions tomberaient l'une sur l'autre à la même vitesse que les 2 autres M ???

Sinon, pour le problème de hclatomic, il doit bien y avoir des solutions approximatives, non ?
@harmoniciste , certes il y a des problèmes de conditions initiales, mais si l'on dérive r(t) on voit que la vitesse est infinie à t=0 , je ne vois pas quelle constante pourrait corriger cela ?

[invitef29758b5]

Je m'explique, comme 2 objets de masse différente tombent à la même vitesse dans un champ de gravitation,

Dans un même champs de gravitation .
Le champs de gravitation vient des masses .
Deux masses plus petite génèrent un champs plus faible .

si l'on dérive r(t)

Pour dériver r(t) , il faudrait avoir une solution analytique .
A t=0 la vitesse est nulle .

[1max2]

@dynamix, pour r(t) je parle de la solution donnée par hclatomic , alors dr(t)/dt= Ct^-1/3 avec donc la vitesse infinie à t=0 ; ce qui est absurde, et pas "rattrapable" . Cette solution est une solution mathématique (il doit y en voir plusieurs ) mais qui ne convient pas en physique ..

Pour le second sujet que j'ai soulevé, oui, c'était une idée idiote de ma part .

Sinon, pour le primo sujet de hclatomic , avec la sonde Rosetta, et le robot Philae , je suppose que l'Agence Spatiale Européenne a pu maintes fois vérifier Newton ...

[harmoniciste]

alors dr(t)/dt= Ct^-1/3 donc la vitesse infinie à t=0 ; ce qui est absurde

Ce n'est pas absurde, vu que la solution de Universus donne r = 0 pour t=0. C'est donc l'instant de la rencontre des deux masses supposées ponctuelles (vitesse et accélération sont bien infinies à ce moment) . Le moment du "lâcher" à vitesse nulle étant antérieur (t négatif).

[1max2]

J'ai repris le travail de mach3 , et finalement je ne trouve pas d'erreur , sa solution pour v (vitesse relative )
me semble bonne, ainsi, déjà hclatomic peut vérifier .
de plus elle est de la forme V²= C/r +C' que donnait universus ...
Sauf erreur probable, en posant m1=6000kg , m2=400000kg ,(ATV et ISS) r0=20m ; r=10 m je trouve donc que quand l'ATV a fait 10m vers l'ISS (distance relative)
la vitesse relative est de 1m/heure , mais on ne sait pas combien de temps l'Atv a mis pour faire ces 10 m .
Il faudrait donc travailler sur cette équation différentielle !
@harmoniciste, l'équation serait à lire à l'envers , la vitesse est infini à l'instant t=0 ( c'est gênant , mais normal, à priori avec Newton) mais avec v de la forme Ct^-1/3 la vitesse ne s'annule qu'à t infini , alors qu'elle devrait s'annuler en un temps fini ! (???)

[0577]

Bonjour,

Comme expliqué dans les messages précédents,
la fonction r satisfait l'équation différentielle


d'où la relation



Le calcul de l'intégrale n'est pas difficile et on trouve



En particulier, on a collision des deux points à



Il est donc possible d'exprimer t(r) en termes de fonctions usuelles mais, comme mentionné dans les messages précédents, ce n'est pas possible pour la fonction réciproque r(t).
Pour de nombreuses questions, connaître explicitement t(r) est suffisant (par exemple, si on veut tracer le graphe de r(t), il suffit de tracer le graphe de t(r) puis de tourner la tête...)

[1max2]

Bravo 0577 , joli travail, le primo -posteur hclatomic va être content , et erreur plus avant , chez moi , l'expression que je donnais est V2 ... ..
Dans ma jeunesse j'ai du résoudre des machins pareils ; je ne sais plus faire....
Il va se faire un plaisir de calculer ce que cela donne numériquement avec l'ISS et l'ATV...

[invite391b927d]

J'ai enfin compris ce que vous vouliez me dire ... Désolé pour le temps que j'ai mis à percuter.

Effectivement l'équation en t^2/3 indique un mobile dont la vitesse n'est jamais nulle (sauf à l'infini) par conséquent en posant les corps immobiles à une distance r, on ne peut être dans ce cas de figure.

A noter cependant que l'équation à résoudre dans le cas que je pose est et pas , ce qui ôte le problème du signe négatif dans la solution (inapplicable) proposée.

Par conséquent il faudra procéder par itérations numériques pour déterminer la trajectoire. Hélas cette méthode nous dit que l'effet est trop faible pour être mesurable en 5' entre l'ATV et l'ISS. En revanche pour un corps de 100g, placé sans vitesse à 10cm d'une masse de 1kg, l'itération m'indique que les deux corps se rejoindront en 1h 40 environ.

Etes-vous d'accord avec cet ordre de grandeur ?

Dans ce cas une expérience avec un cubesat est envisageable. On envoie le cubesat en orbite, on le stabilise, il dépose sans vitesse un petit corps de 100g à 10 cm (grâce à un bras téléscopique), puis il filme ce corps pendant le temps qu'il faut pour que les deux corps se rejoignent. Si la loi de Newton est correcte le processus ne durera qu'1h 40 environ.

Qu'en dites-vous ?

[invite6dffde4c]

Bonjour.
Pensez-vous qu’il faille faire encore des manips pour vérifier la loi d’attraction universelle de Newton ?
Est-ce que tous le satellites et les sondes spatiales n’ont pas prouvé à satiété sa validité ?
Qui voudrait dépenser un kopek pour prouver (mal) que la théorie est valide ?
Sauf les gens qui font des erreurs d’interprétation ou de calcul, comme vous.
Au revoir.

[mach3]

merci à 0577 pour cette belle solution! je m'entêtais à trouver r(t) et m'était résigné (elle ne doit pas avoir d'expression analytique), alors que t(r) se trouve "assez" simplement! le problème est donc résolu!

m@ch3

[harmoniciste]

En particulier, on a collision des deux points à

Ma simulation EXCEL confirme que la rencontre s'effectue bien 36840 s après l'arrêt à 31 m comme votre formule l'indique avec M = 406 tonnes, ce qui ne résoud pas encore le problême r = f(t), mais çà se rapproche.

[invite391b927d]

Bonjour.
Pensez-vous qu’il faille faire encore des manips pour vérifier la loi d’attraction universelle de Newton ?
Est-ce que tous le satellites et les sondes spatiales n’ont pas prouvé à satiété sa validité ?
Qui voudrait dépenser un kopek pour prouver (mal) que la théorie est valide ?
Sauf les gens qui font des erreurs d’interprétation ou de calcul, comme vous.
Au revoir.

Quel positivisme !

L'expérience de David Scott sur la Lune pour prouver le principe d'équivalence de Galilée était elle aussi superflue. Et que dire de cette expérience monumentale refaite sur Terre, bien que David Scott l'ai déjà réalisée. Cependant l'équivalent n'a jamais été fait pour la loi de Newton.

Pour ce qui est des erreurs de calculs, ou d'interprétation, oui cela m'arrive parfois. Que celui qui n'a jamais pêché me jette la première pierre. C'est d'ailleurs en vous demandant respectueusement de me corriger, s'il en était besoin, que je suis venu sur ce forum (voir mes messages). Et je vous remercie de l'avoir fait.

Cordialement

[harmoniciste]

il faudra procéder par itérations numériques pour déterminer la trajectoire. Hélas cette méthode nous dit que l'effet est trop faible pour être mesurable en 5' entre l'ATV et l'ISS.

Non: Cette méthode est précise. C'est ce que j'ai fait et expliqué depuis le début de cette discussion (méthode simple avec EXCEL)

[1max2]

Bonjour, pour ce qui est de l'ISS et de l'ATV qui s'attirent mutuellement , cela n'a pas été dit , mais il faut , selon moi qu'ils soient à la même altitude , sur la même orbite .
S'il y en a un plus bas (plus près de la Terre ) ; il sera sur une autre orbite , et va s'éloigner de côté , car il va devoir tourner plus vite , sauf mal comprenante de ma part !
Alors, on pourrait peut être trouver une solution où l'ATV, légèrement plus bas reste quand même sous influence gravitationnelle de l'ISS , les 2 actions (éloignement , attraction ) se compensant , il y aurait l'équilibre .Qui saurait calculer cette position ?
Ca me rappelle le film gravity où Georges Clooney est plus près de la Terre et "tire" Sandra Bullock placée plus haut vers lui , je ne sais pas si les calculs lui donneraient autant de force , je n'ai pas le temps de les faire là..?

[harmoniciste]

Bonjour,
30 mètres de différence d'altitude, cela fait 30 m /Pi = 10 m de différence de parcours par tour autour de la Terre. Si la période est de 2 h, la vitesse relative due à l'altitude entre l'ISS et l'ATV sera: 10 m / 7200 s = 1,4 mm

[invite6dffde4c]

Bonjour,
30 mètres de différence d'altitude, cela fait 30 m /Pi = 10 m de différence de parcours par tour autour de la Terre. Si la période est de 2 h, la vitesse relative due à l'altitude entre l'ISS et l'ATV sera: 10 m / 7200 s = 1,4 mm

Bonjour harmoniciste.
Petit erreur, ce n’est pas 30 m /PI mais 2.PI.30
Cordialement,

[harmoniciste]

Exact. Merci LPFR