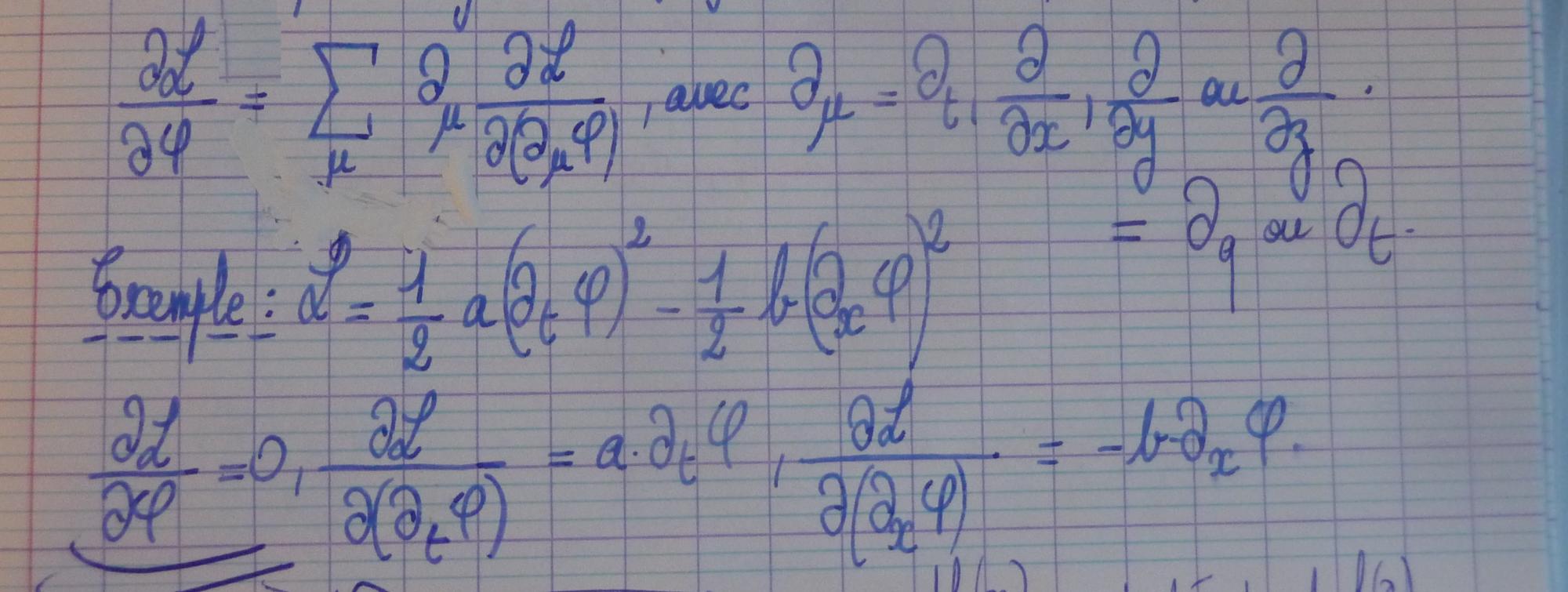q point n'est pas la dérivée de q par rapport au temps ?! (mécanique analytique)

[invite07c97bce]

Bonjour à tous

Etudiant en licence de physique, je viens d'apprendre quelques notions de mécanique analytique.
Après que mon professeur ait voulu démontrer l'équation de Lagrange sur , il a annoncé que q point n'était pas nécessairement la dérivée de q par rapport au temps. J'ai cru comprendre que q point était la dérivée de q par rapport au temps uniquement quand l'équation de Lagrange était vérifiée, mais je n'en suis pas sûr... Pourriez-vous me détailler ce point ?

En vous remerciant d'avance pour vos lumières,

Andreux.
-----

[invite93279690]

Salut,

Il faut parfois se méfier avec les "derivations" des equations d'Euler-Lagrange proposees en licence.

Autant que je sache le sens de est bel et bien celui de la derivee temporelle de par rapport au temps. Ce qui est n'est pas correct par contre c'est de présupposer que est une fonction de (pour se convaincre intuitivement que ce n'est pas le cas, on peut penser a la resolution d'une equation différentielle du second ordre pour laquelle on donne respectivement la valeur initiale de la fonction et sa dérivée sans présupposer que l'une depend de l'autre).

Du coup, il faut écrire le Lagrangien comme étant une fonction de et (et pas uniquement q) pour pouvoir arriver a des conclusions correctes sur l'evolution du système.

[Paraboloide_Hyperbolique]

Bonsoir,

Dans la définition que je connais, est la dérivée totale de par rapport au temps, c'est-à-dire: .
A ne pas confondre avec la dérivée partielle par rapport au temps .

En effet, si (par exemple) , alors

Est-ce cela que le professeur a voulu dire ?

[invite07c97bce]

Salut,

Il faut parfois se méfier avec les "derivations" des equations d'Euler-Lagrange proposees en licence.

Autant que je sache le sens de est bel et bien celui de la derivee temporelle de par rapport au temps. Ce qui est n'est pas correct par contre c'est de présupposer que est une fonction de (pour se convaincre intuitivement que ce n'est pas le cas, on peut penser a la resolution d'une equation différentielle du second ordre pour laquelle on donne respectivement la valeur initiale de la fonction et sa dérivée sans présupposer que l'une depend de l'autre).

Du coup, il faut écrire le Lagrangien comme étant une fonction de et (et pas uniquement q) pour pouvoir arriver a des conclusions correctes sur l'evolution du système.

Mais si q et q point sont supposés déductibles l'un de l'autre par une dérivation / une intégration, cela ne signifie-t-il pas qu'il y a déjà bien une relation entre les deux ?

Bonsoir,

Dans la définition que je connais, est la dérivée totale de par rapport au temps, c'est-à-dire: .
A ne pas confondre avec la dérivée partielle par rapport au temps .

En effet, si (par exemple) , alors

Est-ce cela que le professeur a voulu dire ?

Ce n'est malheureusement pas cela qu'il a voulu dire, j'ai bien repéré cette différence entre les deux dérivations. Merci tout de même.

Pour peut-être mieux expliquer mon problème, dans mon cours je trouve un bref exemple que j'ai joint à ce message (après avoir calculé les dérivées partielles, le professeur applique l'égalité de Lagrange et trouve une équation d'onde, ce qui ne m'a pas posé problème). Et je ne comprends pas pourquoi la dérivée de L par rapport à φ est nulle. D'après mon professeur, c'est car " et φ sont indépendants".

[A voir en vidéo sur Futura]

[invite5ecd70f8]

Ceci n'est vrai que dans le cas de votre exemple, le Lagrangien ne dépend pas explicitement de phi, de ce fait, sa dérivée partielle par rapport à phi est nulle.
A dire vrai, je crois qu'il y a confusion, ce dont vous parlez au début de votre message concernait un lagrangien dépendant des coordonnées généralisées et de leurs dérivées par rapport au temps, ce qui n'est pas le cas pour ce qui est exposé dans votre image, il s'agit plutôt d'un lagrangien dépendant des fonctions du champs et de leurs dérivées.

[invite93279690]

Ceci n'est vrai que dans le cas de votre exemple, le Lagrangien ne dépend pas explicitement de phi, de ce fait, sa dérivée partielle par rapport à phi est nulle.
A dire vrai, je crois qu'il y a confusion, ce dont vous parlez au début de votre message concernait un lagrangien dépendant des coordonnées généralisées et de leurs dérivées par rapport au temps, ce qui n'est pas le cas pour ce qui est exposé dans votre image, il s'agit plutôt d'un lagrangien dépendant des fonctions du champs et de leurs dérivées.

Oui mais le problème ici est que andreuxyoupi presuppose que les dérivées de sont des fonctions de et que donc, comme le lagrangien est une fonction des derivees de , il doit nécessairement être une fonction de .

C'est pourquoi le point que je soulevais est très important. La derivee d'une fonction en un point donne a en fait besoin de deux points de cette fonction pour être définie: est donc une fonctionnelle de (une fonctionnelle très simple certes mais une fonctionnelle quand meme). Cela veut dire que si on s'intéresse au lagrangien (défini pour un instant t donne), il n'y aucune relation directe entre la valeur de la fonction a l'instant et la valeur de la dérivée en ce point. C'est cette absence de relation directe qui fait que l'on peut appliquer les equations d'Euler-Lagrange comme si et étaient des variables indépendantes

[invite93279690]

Mais si q et q point sont supposés déductibles l'un de l'autre par une dérivation / une intégration, cela ne signifie-t-il pas qu'il y a déjà bien une relation entre les deux ?

La procedure de deduction n'est pas directe. Que ce soit l'integration comme la derivation, ce sont des operations qui nécessitent plus d'un seul point de la fonction a intégrer ou deriver pour faire un lien tangible. Dans le lagrangien, il est question de la valeur d'une fonction a un temps t et de la valeur de sa dérivée a ce temps; ces deux valeurs sont totalement indépendantes l'une de l'autre. Tu vois bien d'ailleurs que pour prédire la valeur d'une fonction en x+dx, il te faut connaitre f(x) ET f'(x) qui peuvent avoir des valeurs complètement indépendantes. C'est cette propriété qu'il faut avoir en tete pour comprendre pourquoi on peut appliquer les equations d'Euler-Lagrange comme si la fonction et sa dérivée étaient deux variables indépendantes.

[invite5ecd70f8]

A force de travailler avec, c'est devenu une évidence pour moi, au point où j'en ai oublié l'importance. Merci.

[invite07c97bce]

Merci à tous d'avoir pris le temps de me répondre.

C'est pourquoi le point que je soulevais est très important. La derivee d'une fonction en un point donne a en fait besoin de deux points de cette fonction pour être définie: est donc une fonctionnelle de (une fonctionnelle très simple certes mais une fonctionnelle quand meme). Cela veut dire que si on s'intéresse au lagrangien (défini pour un instant t donne), il n'y aucune relation directe entre la valeur de la fonction a l'instant et la valeur de la dérivée en ce point. C'est cette absence de relation directe qui fait que l'on peut appliquer les equations d'Euler-Lagrange comme si et étaient des variables indépendantes

Ainsi q point est toujours la dérivée de q par rapport au temps, seulement cela ne signifie pas une relation directe entre q et q point, même si ces variables ne sont pas indépendantes. Si je vous suis, l'équation d'Euler-Lagrange n'apporte donc rien de nouveau de ce côté-là.
Le lagrangien de l'exemple vérifie car ce lagrangien ne dépend pas ici de , et, ce, dans la mesure où il ne dépend que de et , des variables n'étant pas liées directement à .

Quelqu'un peut-il me confirmer que je ne me trompe pas ?

[invite93279690]

Ainsi q point est toujours la dérivée de q par rapport au temps, seulement cela ne signifie pas une relation directe entre q et q point, même si ces variables ne sont pas indépendantes.

Les fonctions ne sont pas indépendantes l'une de l'autre; tu ne peux pas changer localement une de ces fonctions sans changer l'autre. Mais du point de vue du lagrangien ce n'est pas l'ensemble de (tous les points de) ces fonctions qui apparait mais seulement leurs valeurs a un instant donne qui sont elles complètement indépendantes l'une de l'autre.

Si je vous suis, l'équation d'Euler-Lagrange n'apporte donc rien de nouveau de ce côté-là.
Le lagrangien de l'exemple vérifie car ce lagrangien ne dépend pas ici de , et, ce, dans la mesure où il ne dépend que de et , des variables n'étant pas liées directement à .

Quelqu'un peut-il me confirmer que je ne me trompe pas ?

moyennant la distinction entre la fonction et la valeur de cette fonction en t oui c'est tout a fait ca.