Cinématique, roue sans glissement

[red17]

Bonjour,

je fais un exercice en cinématique, et je suis confronté à une certaine difficulté.
Voici l'énoncé de l'exercice :
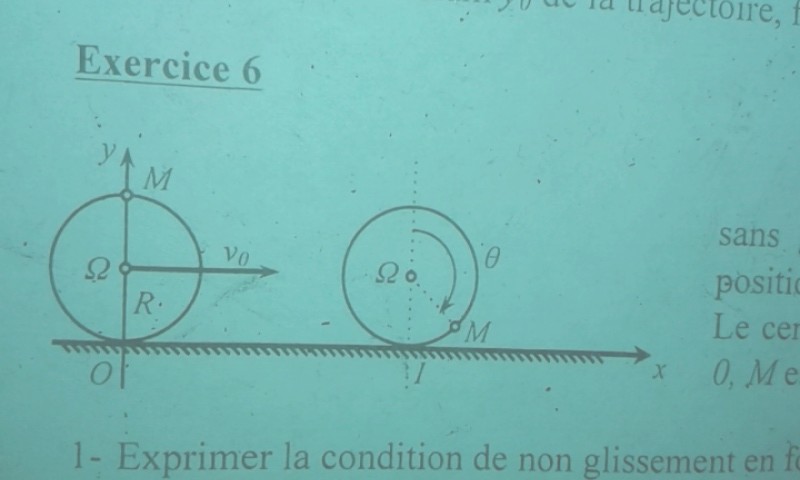
Une roue de rayon et de centre roule sans glisser sur un plan horizontal.
On repère la position du point par l'angle entre et .
Le centre se déplace à vitesse constante
A , est à l'aplomb de et de O

On exprimera les angles en radians.
On notera S la surface qui est en contact ponctuel avec la roue, en I.


1. Exprimer la condition de non glissement en fonction de , et
2. En déduire l'expression de ainsi que les composantes du vecteur dans la base
On posera

Pour la question 1, il faut que la vitesse de glissement soit nulle, et donc que le vecteur vitesse de glissement soit le vecteur nul.
Par définition :


On a :



Il faut donc que :


Mais je n'arrive pas à exprimer cette condition, seulement en fonction des normes.
Les vecteurs unitaires et ne sont pas colinéaires (du moins pas tout le temps)
J'exprime

Mais je suis bloqué...
On obtient ça :

D'où :


Ce qui ne m'avance pas beaucoup.
On peut observer des dérivées de et mais sans plus --'


Quelqu'un pourrait-il m'aider svp ?
Merci d'avance

Cdt
-----

[red17]

J'oublié, voici un schéma qui représente la situation

[Dynamix]

Salut
Cherche en fonction de θ un point de la roue dont la vitesse est identique à celle de la route .

[LPFR]

Bonjour.
Abandonnez les formules 10 secondes et regardez le dessin. Quand la chose aura roulé un tour complet,
- de combien elle aura avancé ?
- de combien elle aura tourné ?
Quelle est la relation entre l’angle tourné et l’avance ?
Au revoir.

[A voir en vidéo sur Futura]

[red17]

Re,

Le point avec ?

Je comprend pas très bien où vous voulez en venir

[red17]

La roue aura tourné de :
La roue aura avancé de :

La relation est donnée par :

[Dynamix]

Ecrire la vitesse du point M en fonction de V0 et de θ
Ensuite dire que pour une certaine valeur de θ , cette vitesse est nulle (condition de non glissement)

[red17]

Comme à t= 0 , et
On peut alors dire que :







Mais la condition de non glissement dépend de et pas de

La vitesse du point M par rapport à ou à ?
L'énoncé suggère que c'est par rapport à , car le point M est repéré en utilisant pour origine.
Par rapport à , il me semble que la vitesse c'est : car le rayon est constant (la roue est supposée indéformable)

On peut exprimer

Dans mon cour, il est dit qu'il n'y a pas glissement quand la vitesse de glissement est nulle.

[red17]

Up ? (10 caract.)

[LPFR]

Re.
Je trouve que c’est un tas équations compliqués pour un problème qui est d’un simplicité totale, si on s’emmerde pas avec des vecteurs unitaires qui rendent les équation illisibles.
Exprimez la position de M (valeurs de ‘x’ et ‘y’) par rapport au centre de la roue en fonction de thêta.
Exprimez la position du centre de la roue en fonction de thêta (avec la condition de non glissement que vous avez déjà trouvée.
Maintenant vous pouvez exprimer la position de M en fonction de thêta.

Si vous avez maintenant besoin d’exprimer la vitesse de M, il suffit de dériver sa position par rapport au temps.

Par contre, vous ne pouvez par exprimer θ(t) car vous ne connaissez pas la nature du mouvement. Il manque une condition dans l’énoncé. .
A+

[LPFR]

Re.
Au temps pour moi.
L'énoncé dit bien de Vo est constante.
Donc on peut bien exprimer thêta en fonction du temps.
A+

[red17]

J'exprime
Autrement dit :



Maintenant, vous voulez que j'exprime la position en fonction de par rapport à O, et je propose :

On se donne
La position de par rapport à est alors :
(cf. condition initiale de )

On a alors :


On peut alors déterminer la position


Pour résumer :

En posant



Et :


Il suffit ensuite de dériver (une fois, puis deux fois) pour obtenir l'accélération de M et sa vitesse par rapport à O.

Merci bcp

[Dynamix]

Tu te noies dans un verre d' eau .
Torseur cinématique : V(m) = V(o) + ****
Condition de non glissement :
Il existe un point M (lequel ?) tel que V(M) = 0
Résoudre V(M) = 0

[Chanur]

La condition de non glissement n'est vraie que pour le point de contact.
Tu cherches une condition pour que tous les points de la roue soient immobiles ?
La seule c'est que la roue ne tourne pas.

Sinon : point de contact => = 0 et ta condition tu l'as écrite depuis longtemps.
Arrête avec tes sinus et cosinus : tu te fais du mal.

[Dynamix]

θ = pi , mon bon Chanur .
Voir l' image .

[Chanur]

θ = pi , mon bon Chanur .
Voir l' image .

Oups. Le lecteur averti aura corrigé de lui-même ...

[red17]

Ok pour la condition de non glissement, mais pour les cosinus : j'ai juste exprimer la position de M par rapport à O, sur la base cartésienne.

Pour ce qui est des Torseurs je viens de l'étudier aujourd'hui en Sii
Mais en physique on a pas du tout fait ça...
On a plutôt dit qu'il n'y a pas de glissement quand le vecteur vitesse de glissement était le vecteur nul (logique) cad quand la vitesse du point M par rapport à O est égal à la vitesse du point I.

Et en effet, il faut que
Donc comme vous le dites la condition de non glissement est vérifiée pour
Autrement dit quand et coïncident

[Dynamix]

Ce qui montre que dans une voiture , quelque soit sa vitesse , il y a toujours une partie qui est immobile .
Pour un train c' est pire , il y a une partie qui recule