Bonjour,
Je suis en train de faire un exercice sur le premier principe.
Voici l'énoncé :
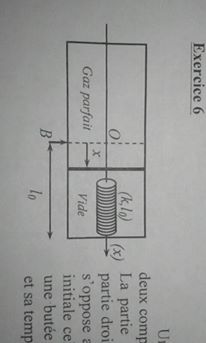
Un cylindre aux parois calorifugées est séparé en deux compartiments par un piston de section. La partie gauche contient
Un ressort de raideur
Dans la situation initiale celui-ci n'est pas tendu et le piston est retenu par une butée B. La pression du gaz est alors
1. Déterminer le volume
2. On supprime la butée B, le système évolue alors vers un nouvel état d'équilibre. Déterminer le déplacement
Question 1, le gaz étant parfait, à l'état initiale on a :
Donc :
Question 2,
A tout instant, on a :
On applique le premier principe aux compartiment de droite, on a :
Le travail étant mécanique :
On a :
Donc :
donc on a :
On obtient donc une équation du second degré en
On peut trouver
Mais il y'a quelque chose qui me gène, c'est le
Si j'ai bon, on devrait tomber sur un truque du genre,
En fait, je suis un peu perdu ...
Je pense pas avoir bon pour le
Quelqu'un aurait une idée ?
Merci d'avance
Cdt
-----