Liaison Lineaire rectiligne créée par 2 cylindres

[Micou38]

Bonjour,
Une petite question concernant une liaison linéaire rectiligne établie entre 2 cylindres.
On dit que 2 cylindres en appui au niveau d'une de leur génératrice sont en liaison linéaire rectiligne (LR pour faire simple).
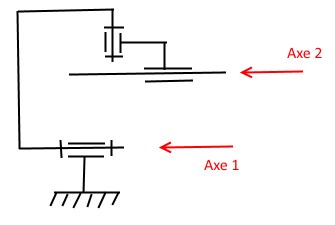
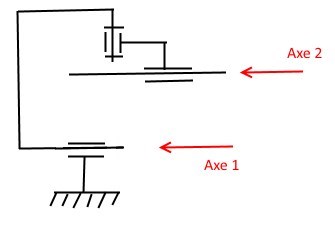
L'illustration est celui des engrenages même si les profils en contact ne sont pas véritablement cylindriques mais des profils en développante de cercle...Passons...
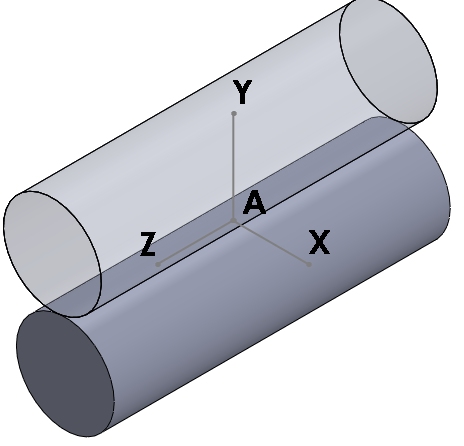
Prenons l'exemple d'une LR de centre A, de ligne de contact selon (A,Z) et de normale (A,Y) => Voir illustration ci-jointe...
Cette liaison normalisée doit avoir 4 degrés de liberté qui sont donc les mouvements relatifs dans le repère local de la liaison tout en conservant ce contact linéique.

Je comprends très bien les degrés de liberté non autorisés par la liaison suivants:
- Translation selon (A,Y) qui supprimerait totalement le contact LR
- Rotation autour de (A,X) qui supprimerait le contact linéique au profit d'un contact ponctuel...

Je comprends également très bien les degrés de liberté suivants:
- les 2 translations dans le plan tangent du contact, soit selon (A,Z) et selon (A,X)
- la rotation autour de (A,Z)

Mais je coince sur la rotation autour de (A,Y) car une telle rotation supprimerait le contact linéique au profit d'un contact ponctuel...
Les axes de cylindres n'étant plus parallèles, le contact ne peut plus être linéique.
Dans le cas d'une LR entre un cylindre et un plan, il n'y a pas ce problème mais là, entre 2 cylindres, je tique...
Quelqu'un peut-il me convaincre que cette rotation est possible avec un tel contact et que la liaison entre 2 cylindres peut donc effectivement se modéliser par une liaison normalisée de type LR ?? avec les 4 degres de liberté que cela implique ??

Merci d'avance a ceux qui se pencheront sur ce petit problème...

-----

[le_STI]

Salut.

.....Mais je coince sur la rotation autour de (A,Y) car une telle rotation supprimerait le contact linéique au profit d'un contact ponctuel... ....

Dans l'absolu ce n'est pas le cas.

Un contact ponctuel doit permettre une rotation pure autour des 3 axes, mais dans le cas de deux cylindres dont les axes ne sont pas parallèle, ce n'est pas vrai.
Un exemple concret : essaye d'incliner un des cylindres en ne déplaçant pas le point de contact (ce qui doit être possible avec une liaison ponctuelle)...

Je crois que tu te trompes en voulant définir un type de liaison (ici linéaire rectiligne) par rapport à la géométrie de la surface de contact (ici un segment).

D'ailleurs, dans ton exemple, la translation sur X n'est pas possible non-plus puisque dans ce cas les deux cylindres ne seraient plus en contact (on parle du mouvement relatif d'un cylindre par rapport à l'autre), pas plus que la rotation autour de Z (je parle bien de Z tel que représenté sur le dessin, pas de l'axe d'un des cylindres).

Pour moi, si tu considérais l'axe Z confondu avec l'axe du cylindre du haut, on s'approcherait d'une liaison linéaire rectiligne : translation sur X et Z possible (dans le cas où les axes des cylindres ne sont pas parallèles), rotation autour de Y et Z possible, translation sur Y impossible (si on impose le contact entre les cylindres), rotation pure autour de X impossible.

[Mecanik77]

Bonjour,

Bonjour,
L'illustration est celui des engrenages même si les profils en contact ne sont pas véritablement cylindriques mais des profils en développante de cercle...Passons...

C'est justement parce qu'ils ont un profil en développante de cercle qu'on considère qu'ils sont en contact suivant une ligne.

Mais je coince sur la rotation autour de (A,Y) car une telle rotation supprimerait le contact linéique au profit d'un contact ponctuel...

En es-tu sûr?
De mon côté j'y vois deux contacts ponctuels...Donc une ligne.

[Micou38]

Bonjour et merci de vos réponses.

D'ailleurs, dans ton exemple, la translation sur X n'est pas possible non-plus puisque dans ce cas les deux cylindres ne seraient plus en contact (on parle du mouvement relatif d'un cylindre par rapport à l'autre), pas plus que la rotation autour de Z (je parle bien de Z tel que représenté sur le dessin, pas de l'axe d'un des cylindres).

Pour moi, une translation dans la direction X d'un cylindre (aussi petite soit elle) entraine une requalification du plan tangent du contact, donc une nouvelle direction X qui finalement, reste tangent au cylindre donc il ne me parait pas incohérent d'admettre cette translation relative selon X (direction X qui varie lors du mouvement relatif car le repére de description est bien un repère local). Je tiens également ce raisonnement pour la rotation autour du Z figurant sur le dessin (Direction Z qui se déplace sur des génératrices successives du cylindre) et qui entraine une requalification du repère local, mais pour ces 2 degrés de liberté, les axes de cylindres restent parallèles !!
En revanche, une rotation relative autour de Y désaligne les axes des cylindres donc la construction de repère local devient, selon moi, impossible, en tout cas, pour une linéaire rectiligne...

De mon côté j'y vois deux contacts ponctuels...Donc une ligne.

Ben justement, je ne les vois pas ces 2 contacts ponctuels, sinon, je serais content car effectivement 2 points définissent une ligne !! Même une éventuelle tangence entre les 2 surfaces cylindriques dont les axes seraient désalignés me contenterait en partant du fait qu'une tangence en un point est la position limite lorsque 2 points tendent l'un vers l'autre. Mais j'avoue que je ne suis encore pas convaincu...

[A voir en vidéo sur Futura]

[Dynamix]

Salut
Ta liaison supprime bien 3 degrés de liberté .
Regarde les liaisons qui sont nécessaires à maintenir le contact entre deux roues d' engrenage .
Il faut roulements .

[espacetempsrayonnant]

Bonsoir,

Je pencherai sur une liaison linaire transversale.(mais je peux me tromper)

Je pense a l'effet Magnus sur Wikipedia.

Bonne soirée
Cordialement

[Dynamix]

Je pense a l'effet Magnus sur Wikipedia.

Quel rapport avec un engrenage ?

[Mecanik77]

Ben justement, je ne les vois pas ces 2 contacts ponctuels, sinon, je serais content car effectivement 2 points définissent une ligne !! Même une éventuelle tangence entre les 2 surfaces cylindriques dont les axes seraient désalignés me contenterait en partant du fait qu'une tangence en un point est la position limite lorsque 2 points tendent l'un vers l'autre. Mais j'avoue que je ne suis encore pas convaincu...

Au temps pour moi, l'image ne s'affichait pas là où j'étais et j'étais convaincu que tu parlais d'un contact intérieur.
Ta question est tordu, mais tu enfreints une règle essentielle, tu romps le contact linéaire rectiligne.
Dés lors tout est possible, par exemple si on poursuit le mouvement d'une des translations qu'autorise une liaison appui-plan entre deux pièces on va tomber sur une linéaire rectiligne (avant le basculement de l'une par rapport à l'autre sous l'effet de la gravité) puis on va arriver à 6 degrés de liberté (lorsque les deux pièces ne seront plus en contact).
Pour moi c'est la même chose.

[Mecanik77]

Bonsoir,

Je pencherai sur une liaison linaire transversale.(mais je peux me tromper)

Inconnue au bataillon...

[le_STI]

Pour moi, le problème est pris à l'envers.
Micou38 cherche a trouver un système qui représente une liaison (linéaire rectiligne) alors que dans le principe on définit des liaison par rapport à un système existant.

L'assemblage de ces deux cylindres est par exemple représenté par l'ensemble de liaisons ci-dessous (si on leur impose le maintien en contact):

[le_STI]

Je voulais dire "...on utilise des liaisons pour représenter un mécanisme existant."

[Dynamix]

Il y a une liberté de trop sur ton croquis .
Il ne devrait y avoir de libre que la rotation et la translation sur l' axe x .

Soit 2 paliers sans appui .

[le_STI]

Je cherche à représenter deux cylindres qui seraient en permanence en contact, tels que représenté sur l'image de Micou38.
Dans ce cas, sont possibles:
-translation+rotation suivant l'axe du cylindre du haut (via le pivot glissant du haut)
-rotation autour de l'axe Y représenté par Micou38 (via pivot du haut)
-translation+rotation de la tige du haut suivant l'axe de la tige du bas (via le pivot glissant du bas)

J'avais même oublié un degré de liberté.

[Dynamix]

-translation+rotation suivant l'axe du cylindre du haut (via le pivot glissant du haut)
-translation+rotation de la tige du haut suivant l'axe de la tige du bas (via le pivot glissant du bas)

C' est les mêmes deux degrés de liberté : translation et rotation x .
Peu importe celui qui se déplace .

Je cherche à représenter deux cylindres qui seraient en permanence en contact, tels que représenté sur l'image de Micou38.

Sur l' image de Micou38 ils sont en contact linéique .
La rotation y fait perdre le contact linéique qui devient ponctuel .

[le_STI]

Je veux représenter deux cylindres en contact mais dont la seule contrainte serait le fait qu'ils doivent rester en contact. On peut donc les "croiser" (en tournant autour du pivot d'axe vertical sur mon schéma), puis déplacer le cylindre du haut selon l'axe de celui du bas par exemple (d'où l'intérêt du pivot glissant du bas).

[Micou38]

Je cherche à représenter deux cylindres qui seraient en permanence en contact, tels que représenté sur l'image de Micou38.

Ton schéma est intéressant car effectivement, ce système reprend bien les 4 degres de liberté d'une linéaire rectiligne (2Trans. et 2Rot.) avec un repère local qui "suit" l'axe2 si on imagine que l'axe1 est fixe MAIS ce système ne garantit pas un contact linéique permanent. Et comme l'écrit MECANIK77:

Ta question est tordu, mais tu enfreints une règle essentielle, tu romps le contact linéaire rectiligne.

D'où la reponse de DYNAMIX, qui est juste:

La rotation y fait perdre le contact linéique qui devient ponctuel.

Quant à la derniere réponse de le_STI:

mais dont la seule contrainte serait le fait qu'ils doivent rester en contact.

Je suis d'accord, MAIS le contact n'est plus linéique et ma question initiale est: A-t-on le droit d'écrire que 2 cylindres en appui sur leur génératrice (un peu comme dans un engrenage) sont en liaison Linéaire Rectiligne (LR) ? (car ce n'est vrai que lorsque les axes de cylindres sont parallèles...).
A cela je répondrai OUI si les axes de cylindres restent parallèles, mais cela revient a interdire la rotation autour de l'axe Y donc le tableau des degrés de liberté n'est plus celui d'une LR donc on a en quelque sorte une "fausse LR". Non ??

[Mecanik77]

Non, la seule exception c'est lorsque les deux axes sont orthogonaux. Mais si tel était le cas on parlerait alors d'une liaison ponctuelle...On tourne en rond.

[Dynamix]

En cherchant les efforts transmissibles , j' aboutis à des contradictions .
J' en viens à la conclusion que ce n' est pas une liaison .
La liaison entre les deux cylindre doit être de type "pivot glissant" et n' a rien à voir avec "cylindre/plan" (=LR)

[le_STI]

Le schéma que j'ai fait est le schéma cinématique de deux cylindres en contact permanent.

Je n'ai jamais dit que cela correspondait à une linéaire rectiligne, je voulais justement démontrer le contraire, puisque j'ai écrit que "l'assemblage de ces deux cylindres est par exemple représenté par l'ensemble de liaisons ci-dessous (si on leur impose le maintien en contact)".

Par ailleurs, Mecanik77, la liaison devient ponctuelle dès que le parallélisme est perdu, pas seulement lorsque les axes sont orthogonaux.

[Mecanik77]

Pour moi l'étendu de la ligne de contact diminue certes mais elle reste une ligne jusqu'à ce que les deux cylindres soient perpendiculaires.

[Dynamix]

Pour moi l'étendu de la ligne de contact diminue certes mais elle reste une ligne jusqu'à ce que les deux cylindres soient perpendiculaires.

Ce n' est valable que pour toi .
En géométrie , par exemple , c' est faux .
Place un plan tangent aux deux cylindres , ça te donne 2 droites sécantes .

[Mecanik77]

Belle image, je suis d'accord avec toi.

[Lydish]

On a la définition suivante d'une dent :


La modélisation vient de la forme de la dent. Ce ne sont pas 2 cylindres en contact, mais 2 formes cylindriques différentes pour un flanc de dent. Alors, lorsqu’elles sont en contact, on estime que l’une a une surface cylindrique en contact avec un plan (dans le cas où on cherche à tourner autour de z, sinon cela n’a pas d’intérêt bien entendu). Je crois que c’est cette raison qui pousse à préserver la rotation autour de z dans la liaison mécanique qui représente les dents des engrenages. Dans la réalité, les formes des dents des engrenages sont faites pour préserver ce contact linéique même dans la rotation autour de cet axe. Autrement, les efforts transmis seraient trop importants. Les engrenages sont développés pour encaisser ces efforts.

Dans tous les cas, l’engrenage n’est pas représenté par une liaison linéaire rectiligne dans les schémas cinématiques (c'est la liaison pour le contact entre 2 dents d'ailleurs, pas l'engrenage complet), il a sa propre représentation. La liaison linéaire rectiligne pour l'engrenage n’a d’intérêt que lorsque l’on étudie les engrenages de façon moins macroscopique (au niveau des dents).

En espérant que cela serve à d'autres qui verront ces messages.
A+ !