Bonsoir tout le monde ,
c'est mon premier thread et celui ci concerne quelques exercices de bases sur les coordonnées polaires ,je vous remercie d'avance pour votre attention et pour l'aide que vous m'accorderez .
voici les questions qui se posent a moi :
1-Trouvé l'angle thêta , θ en dégrées avec les coordonnées cartésiennes x et y ,on nous donne également TAN(31°)=0.6=3/5.
On cherche θ tel que :
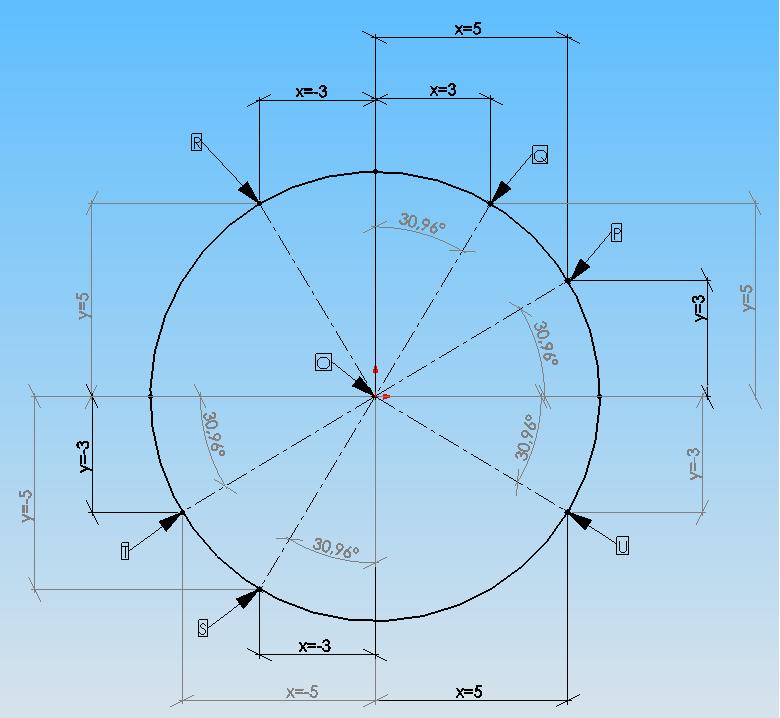
1)x=3 y=5
2)x=-3 y=5
3)x=5 y=-3
4)x=-3 y=-5
5)x=-5 y=-3
Je sais que A=Arctan(y/x) mais sa serait trop simple avec cette formule , surtout qu'elle a été élaborée a partir d'un développement limité autours de 0 il me semble .
Donc je me suis dit que l'on doit utilisé l'indication dans l'énoncé , TAN(31°)=0.6=3/5 et j'en déduis que pour la question 5)
on a θ =31° , pour la 3 θ=-31°.Ensuite pour 1),2) et 4) je me suis dit que l'on peut faire 1/TAN(31°)=5/3 et 1/TAN(31°)=5/-3 =-5/3.
Du coups j'hésite car l'inverse de la tangente d'un angle me donnera-t-il un angle ?
Merci de m'aider pour cette première question qui est la suivante , mon raisonnement est-il correct ? je me doute que vers la fin il y a une magouille .
2-Ici , un exercice ou l'on nous demande de dessiner le mouvement du point étudié ( avec p(t)=v0t et θ(t)=wt), puis de déterminer la vitesse avec des coordonnées polaires puis cartésiennes et enfin de dessiner un vecteur vitesse a 90°,180°,-90°.
Pour le dessin j'ai fais une spirale car le module p(t) augmente en fonction du temps et que l'angle θ (t) aussi , jusque la rien de bien compliqué .
Je vais la faire courte de peur d'écrire un trop gros pavé .
Vitesse en polaire : v(t)=d(p(t))/dt*up(t) + d(θ(t))/dt*Uθ*v0t avec d(θ (t))/dt = w donc v(t)=v(t)=v0*up(t) + w*Uθ*v0t
Vitesse en cartésienne : v(t)=v0(cosθ i+sinθ j)+w*v0t(-sinθi+cosθj).
Je pense que mes expressions sont bonnes , vous allez me dire '' mais il veut quoi au juste ? '' , j'y viens !
Quand je dois placer mes vecteur vitesses (approximativement) , a 90°,180°,-90°je remarque que le vecteur vitesse a ces différents angles augmente car dans v(t) on a v0 pour up ce qui est constant mais on a w*v0t pour uθ ce qui veut dire que cela augmente .
J'ai alors dessiner des vecteurs pas très tangents a la courbe dessinée par la spirale mais j'imagine qu'a -90° il devient un peu plus tangent car uθ devient de plus en plus grand devant up.
La aussi je me demande si mon raisonnement est juste et tant qu'on y est j'ai du mal a me suivre moi même car p(t)=v0t donc la vitesse a l'air intuitivement(pour moi) constante mais je vois bien que la vitesse en uθ augmente et d'un coté je me dit que c'est logique car si on prend un t trèèèèèèès trèèèès grand , la spirale aura l'air d'une droite pour nous(sur un coté de la spirale, comme un gros zoom quoi) et cela montre que l'accelération normale est beaucoups plus petite que l'accélération tangentielle sur un point de la spirale .
Je vous remercie encore d'avance pour l'attention que vous m'accordez .
Ps:je suis en Licence 1 Maths-Physique-Info a Paris-Sud .
-----