Mécanique des fluides : Vidange d'une conduite sous pression

[invite38644575]

Bonjour,

Je vous faire part d'un problème de mécanique des fluides que je rencontre et qui me rend assez fou

Le problème est le suivant :

Je dispose d'une conduite de gaz naturel (masse volumique : 0.7 kg/m3) en PEHD d'une longueur de 2000 m isolée par sécurité par deux postes de fermeture à ses extrémités.
Il n'y a donc plus de débit, la pression interne est constante à l'état initial, j'estime le fluide incompréssible. On ouvre une vanne de détente qui a pour but de vidanger la canalisation (dvanne=0.05m) elle même de diamètre intérieur 0.13m et 0.16m extérieur.

L'objectif est de déterminer en combien de temps la conduite sera vidangée et que selon les normes, ce temps doit être inférieur à 20 minutes. (Le système est conforme à cette norme d'après un organisme externe qui a "étudié le problème")

En applicant le th de Bernoulli entre un point A situé dans la canalisation et un point B au niveau de la vanne de détente je trouve une expression de la vitesse en B
(la différence de hauteur entre A et B étant négligeable)

VB = √((2(PA-PB))/ρ)

Comme Q = S*V, V = Q / S et Q = dVol / dt (Vol étant le volume de gaz à l'intérieur de la conduite)

J'obtiens une expression de dt = dVol / (VB*S) ;

En prenant une pression PA de 8 bar et une pression PB = Patm = 1 bar ; je trouve un temps d'environ 2800 secondes soit plus de 46 minutes. Je ne comprend pas comment cet organisme a pu trouver un temps de vidange inférieur à 20 minutes.

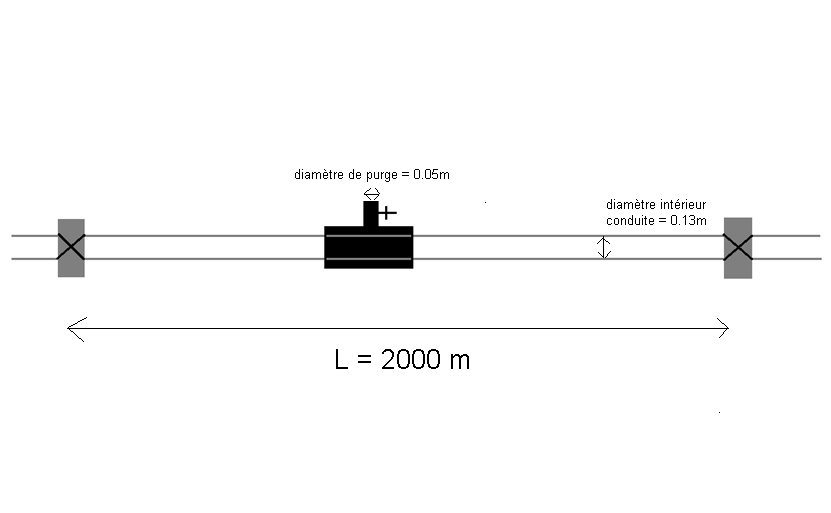
Je vous joins un schéma si ça peut vous être utile.

Je pense que le problème est plus complexe que ça puisqu'il faut tenir compte de la diminution du volume de gaz dans la conduite (assimilable à un réservoir) qui varie en fonction du temps et de la diminution de pression que ne doit pas être linéaire et qui varie elle aussi en fonction du volume (et donc du temps). Bref, beaucoup de variables et je m'y perd un peu.


-----

[invite6dffde4c]

Bonjour et bienvenu au forum.
Admettons que la canalisation se comporte comme un réservoir et que l’on peut négliger la vitesse à donner au gaz à l’intérieur.
Partez de la vitesse ‘v’ que vous avez trouvée.
Puis :
dm = -ρ.v.s.dt
où ‘s’ est la surface de sortie (5 cm de diamètre) et ρ est la densité :
ρ = m/V
où ‘m’ est la masse de gaz restant dans volume V de vos 2 km de tuyau.
Loi des gaz parfaits : PV = nRT.
‘n’ est le nombre de moles : m/M où M est la masse molaire (en kg) de votre gaz.
Donc, P = (m/M)(1/V)RT
Remplacez ρ et P dans l’expression de ‘dm’.
Vous obtiendrez une équation de la forme dm/m = -A.dt
Qui est intégrable immédiatement est vous donne une solution de la forme :
m = m_o exp(-At).

Vous n’obtiendrez pas un temps de vidage, mais une constante de temps de vidage. Probablement on peut considérer que le tube est vide après 5 constantes de temps.

J’ai triché un peu en utilisant la pression absolue P, alors que dans Bernoulli, c’est la différence de pression entre l’intérieur et l’extérieur. Si on prend la différence, le résultat sera meilleur, mais les équations se simplifieront moins.
Au revoir.

[invite38644575]

Alors, si je reprend votre explication

v = √((2(PA-PB))/ρ) simplifiable ) v = √(2P/ρ)
dm = - ρ v S dt (pourquoi le signe - devant ρ d'ailleurs ? Est-ce parce-que l'on perd du débit au fur et à mesure du temps ?)
ρ = m/V
Donc dm = - m/V * v * s dt ; dm/m = -(vS/V) dt

P = (m/MV)RT donc en injectant P dans la formule de la vitesse ton obtient v = √(2((m/MV)RT)/(m/V))
En simplifiant les m et V on garde v = √(2RT/M)

On retrouve dm/m = - (√(2RT/M)*S) / V) dt soit dm/m = -A.dt
En intégrant cette expression on obtient ln m = -At donc m = exp(-A.t)

Je ne retrouve juste pas le m_o, est-ce une constante d'intégration que j'ai oublié ?