Bonjour,
Je suis actuellement en L3 à l'université de Toulouse et j'ai commencé à lire des livres sur la physique des plasmas.
Je réalise donc des exercices pour mon propre intéret et j'ai trouvé un TD de plasmas où je bloque sur un calcul du théorème de Gauss que je maitrise pourtant d'habitude.
L'énoncé est dans la pièce jointe, je ne sais vraiment pas faire donc si vous pouvez me donner des pistes etc... ce serait sympa.
Merci d'avance,
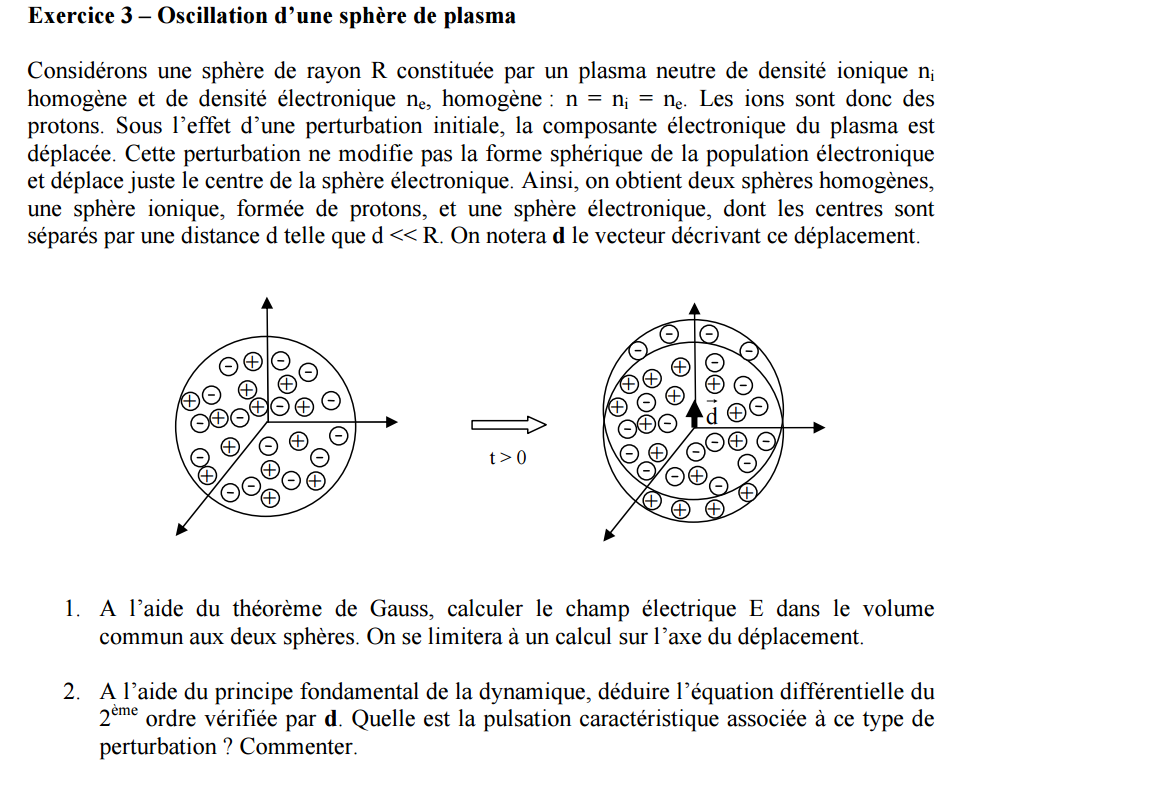
-----



 (fleche sur r) et avec q= e
(fleche sur r) et avec q= e