Bonjour,
Voici un petit paradoxe. Je n'arrive pas à trouver d'explication satisfaisante.
Considérons un référentiel inertiel R et un référentiel R’ se mouvant à la vitesse V par rapport à R. Pour simplifier, on suppose que l'axe des X de R coïncide avec l'axe des X de R’.
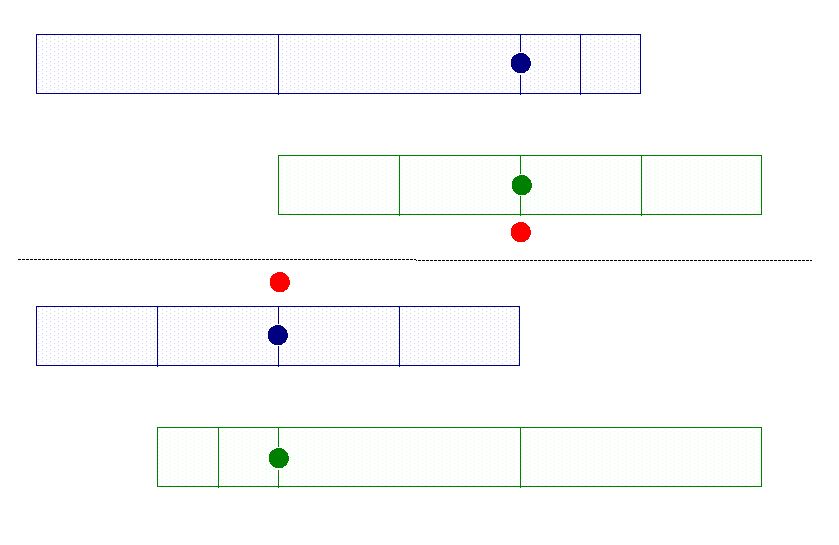
On munit R de deux observateurs fixes A et B séparés par la distance d. Ces deux observateurs possèdent chacun une horloge fixe. ON suppose également un observateur C fixe par rapport R’ possèdant sa propre horloge.
Lorsque C passe devant A, ces deux observateurs synchronisent leur horloge à 0. De plus, au même moment, A envoie un signal lumineux B afin que B synchronise sont horloge avec celle de A.
Lorsque C passe devant B ces deux observateurs comparent leur horloge.
En théorie, l'horloge de B indique un temps plus grand que l'horloge de C.
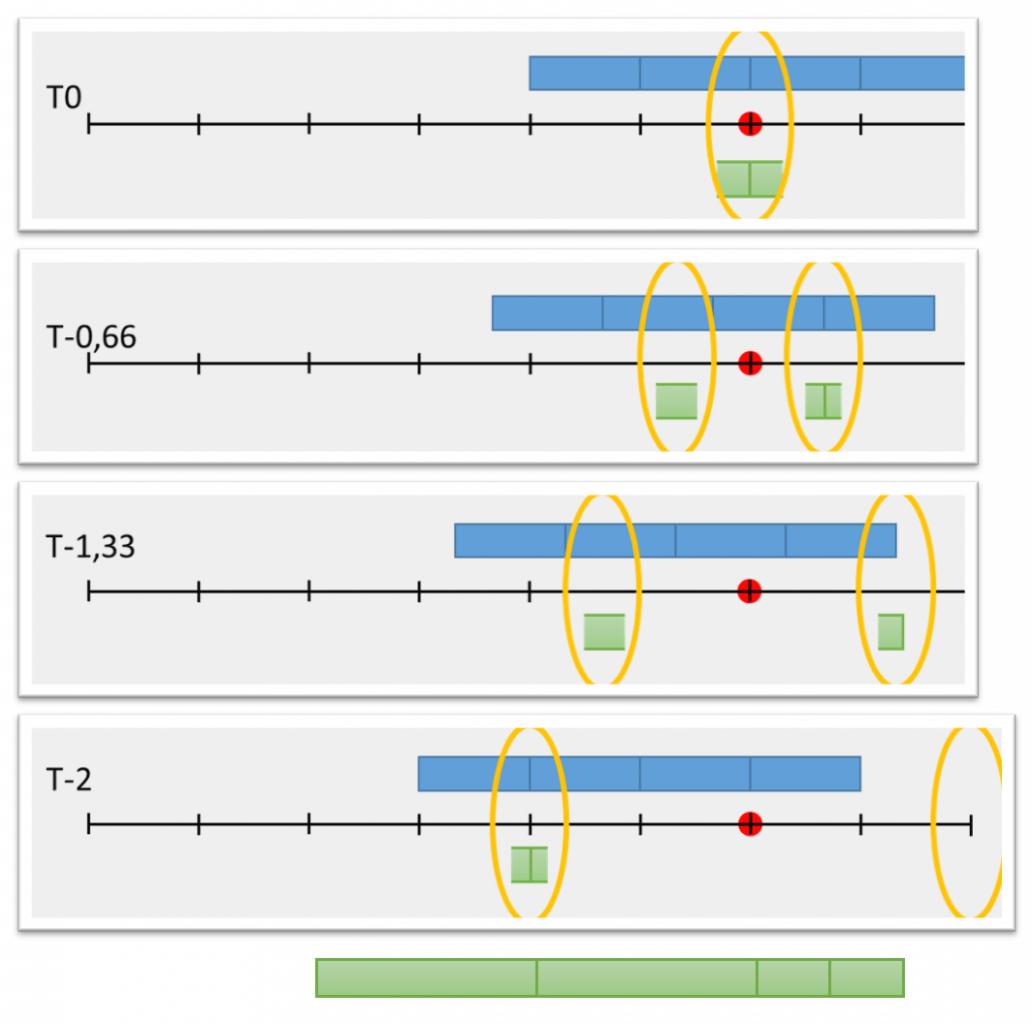
Mais on peut faire une expérience semblable en considérant cette fois-ci une deuxième horloge fixe D dans le référentiel R’ et en considérant que c'est R qui se déplace à la vitesse V par rapport R’. on répète alors la procédure de synchronisation B avec D puis C avec D. Lorsque B passe devant C son horloge devrait indiquer un temps plus petit.
Comment résoudre ce paradoxe? Dans un livre sur la relativité restreinte, l'auteur dis que la situation n'est pas symétrique car il y a plusieurs horloges dans un référentiel et une seule dans l'autre mais ce n'est pas une explication satisfaisante...
Merci
-----