La décharge d'un condensateur chargé négativement

[invite06ca88e4]

Le problème de la bobine est que le courant ne peut changer brutalement. En effet si di/dt est grand la tention aux bornes de la bobine devient tres grande.

Lorsque le courant est établit , le courant est alors limité par les résistances ou les charges des condensateurs par exemple.

il ya une continuité de courant pour la bobine
-----

[calculair]

En effet , cela impose donc qu'a l'instant 0 le courant est nul.

Par ailleurs il est plus facile d'établir l'equation différentielle en i

Quand tu auras l'équation du courant, par intégration tu auras la loi de variation de la charge Q du condensateur.

Comme le condensateur et la self sont des éléments non dissipatifs l'énergie restera constante ( Pas d'amortissement )

Je pense que tu es prêt de la solution

il ya une continuité de courant pour la bobine

[invite06ca88e4]

En effet , cela impose donc qu'a l'instant 0 le courant est nul.

Par ailleurs il est plus facile d'établir l'equation différentielle en i

Quand tu auras l'équation du courant, par intégration tu auras la loi de variation de la charge Q du condensateur.

Comme le condensateur et la self sont des éléments non dissipatifs l'énergie restera constante ( Pas d'amortissement )

Je pense que tu es prêt de la solution

ui merci bcp
il ya quelque chose qui m occupe tjrs lors de la resolution de l'exercice
c est que je sais pas quand fait entrer les signes moins et les signes postif
est ce que tjrs une convention generateur est equivalent a dire que tt les relations du cours seraient avec un _ moins ?

[calculair]

Bonjour

Les signes c'est une affaires de convention.

Si tu prends le sens du courant identique à celui des électrons ( D'habitude c'est la convention contraire ) Le courant sort du pôle - du condensateur

Pour ce qui concerne la self la loi de Lenz nous dit que cette dernière s'oppose au courant qui la traverse ( Ul = - L di/dt ) Cela signifie que Ul aura le signe - du coté ou le courant du condensateur arrive

Ainsi la somme des tensions quand tu parcours la boucle est nulle Uc + Ul = 0

J'espère que tu as résolu l'equation différentielle et que tu as trouvé le régime oscillatoire ...

[invite5a48ffd1]

Lire ceci:
https://ics.utc.fr/Electricite/Elect.../cours_13.html

Bien comprendre que le condensateur (ou la self) sera tantôt récepteur ou générateur.

[invite06ca88e4]

1.lorsque on ferme l'interrupteur k .quel phénomène se produit dans le circuit ?
Oscillations électriques libres non amorties [r nulle]
2. Établir l’équation différentielle vérifiée par l armature négative du condensateur
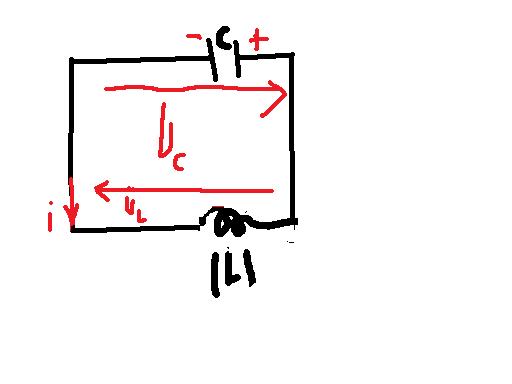
voila les conventions que j'ai choisie
alors ona d apres la loi d 'additivite des tentions
UL+Uc =0
Ldi/dt+_q/c =0
notons q la charge de l'armature negative . porquoi j'ai mis le moins ? car uc =q/c si q1 est la charge de l'armature positive puique a chaque intant ona q1 + q =0
pou la tention au bornes de la bobine ldi/dt =_lcduc/dt . le signe _ car toujours on parle d'une charge negative
en fin on aura q/lc+dq/dt =0. s'il vous plait est ce correct ? j ai essaye mon max de comprendre cela.
sinon vous pouvez me proposez une serie d'exercices corrigées pour cela . merciiiiii

[invite06ca88e4]

[invite5a48ffd1]

Pour éviter toutes confusions, il est préférable d'adopter pour Uc un flêchage inverse, ou d'indiquer -Uc dans votre dessin.
La tension aux bornes de C est donnée négative dans les conditions initiales et L est déchargée (Io=0).
A la fermeture de K, UL va s'opposer à i, votre représentation est juste.

[invite5a48ffd1]

Il faut écrire que -Uc+UL=0

Soit -Uc+Ldi/dt=0

i=dq/dt et q=C.Uc, que vous pouvez traduire par: un courant est un déplacement de charges par rapport au temps et il n'y a pas de discontinuité de tension aux bornes d'un condensateur.

=> -q/C+Ld(dq/dt)/dt = Ld²q/dt² -q/C=0

[stefjm]

Bonsoir,
Nan...
Une erreur de signe quelque part.
La réponse ne peut pas être en exponentielle divergente...

[invite06ca88e4]

Pour éviter toutes confusions, il est préférable d'adopter pour Uc un flêchage inverse, ou d'indiquer -Uc dans votre dessin.
La tension aux bornes de C est donnée négative dans les conditions initiales et L est déchargée (Io=0).
A la fermeture de K, UL va s'opposer à i, votre représentation est juste.

mais moi j ai fait uc avec flechage inverse.

[invite06ca88e4]

Bonsoir,
Nan...
Une erreur de signe quelque part.
La réponse ne peut pas être en exponentielle divergente...

divergeante ?

[stefjm]

L'équation différentielle proposé par Chtulhu a comme solution A.e^(w0.t)+B.e^(-w0.t) dont le premier terme part à l'infini quand t tend vers l'infini.

[invite5a48ffd1]

Oui en effet, c'est i=-dq/dt
Merci de l'avoir vu

[invite5a48ffd1]

L'équation est donc d²q/dt² + q/LC=0

[calculair]

Voir mon message N°34
Avec tes conventions Ul doit être dans l'autre sens de façon que Ul + Uc = 0
-Ldi/dt + Q/c = 0

- Ld2i /dt2 +dQ/dt *1/C =0

-Ld2 i/dt2 + I/C = 0

Une solution de la forme i = A sin (wt +a) peut être solution

Identification avec l'équation
di/dt = AW cos(wt + a)

d2i/dt2 = - AW2 sin ( wt+a)

En identifiant - LAW2 sin( wt +a) + A /C sin( wt +a ) = 0
ou
AW2 Sin( wt +a) = A/(CL) sin ( wt +a )

donc W = Racine ( 1/(CL)

les conditions initiales vont permettre de définir les constantes A et a

Pour t = 0 le courant est nul donc a = 0

A va dépendre du courant max et de la charge initiale du condensateur

Q = Somme A sin( wt) dt de t = 0 à T/2

Pièce jointe 358535Pièce jointe 358535

[stefjm]

-Ld2 i/dt2 + I/C = 0

Nan!...
Erreur de signe quelque part...
La réponse ne peut pas être en exponentielle divergente.

Une solution de la forme i = A sin (wt +a) peut être solution[...]

Ben non, puisqu'il y a une erreur de signe dans l'équation différentielle!

[invite06ca88e4]

L'équation est donc d²q/dt² + q/LC=0

effectivement ca ce que j'ai trouvé

[invite5a48ffd1]

Pour ma part j'ai toujours opté pour la convention récepteur c'est à dire quand le courant entre dans le modèle et la tension fléchée du potentiel le plus bas vers le potentiel le plus élevé (là où se trouve la flèche), et la convention générateur pour le courant sortant du modèle avec la tension fléchée du potentiel le plus bas vers le potentiel le plus élevé (là où l'on met la flèche).
Dans cet exercice, le condensateur est générateur (c'est lui qui fournit le courant à la self) mais sa tension est négative donc je ferai sortir le courant tel qu'indiqué sur le schéma de parklee et orienterai la tension dans le même sens que i, puis i entre dans L, avec UL orienté à l'opposé du sens de i (L est récepteur).
Ainsi nous aurions écrit que UL-Uc=0 (c'est plus intuitif je trouve) => Ldi/dt - q/C avec i=-CdUc/dt => i=-dq/dt => Ld²i/dt²+q/C=0

On retrouve bien le même résultat.
L'essentiel est de choisir la convention avec laquelle on est le plus à l'aise et de s'y tenir

[stefjm]

Un façon de ne pas merder les signes est de rester toujours toujours toujours avec la même convention, par exemple

récepteur : flèche courant et tension tête bêche : u=+R.i ; u=+L.di/dt ; i=+C.du/dt

et comme dit LPFR, de réfléchir.

[invite06ca88e4]

Pour ma part j'ai toujours opté pour la convention récepteur c'est à dire quand le courant entre dans le modèle et la tension fléchée du potentiel le plus bas vers le potentiel le plus élevé (là où se trouve la flèche), et la convention générateur pour le courant sortant du modèle avec la tension fléchée du potentiel le plus bas vers le potentiel le plus élevé (là où l'on met la flèche).
Dans cet exercice, le condensateur est générateur (c'est lui qui fournit le courant à la self) mais sa tension est négative donc je ferai sortir le courant tel qu'indiqué sur le schéma de parklee et orienterai la tension dans le même sens que i, puis i entre dans L, avec UL orienté à l'opposé du sens de i (L est récepteur).
Ainsi nous aurions écrit que UL-Uc=0 (c'est plus intuitif je trouve) => Ldi/dt - q/C avec i=-CdUc/dt => i=-dq/dt => Ld²i/dt²+q/C=0

On retrouve bien le même résultat.
L'essentiel est de choisir la convention avec laquelle on est le plus à l'aise et de s'y tenir

parfait ui je comprends bien maintenant . merci infiniment
juste une petite question : dans un montage que voulez vous dire avec là ou le potentiel élevé?

[invite06ca88e4]

Un façon de ne pas merder les signes est de rester toujours toujours toujours avec la même convention, par exemple

récepteur : flèche courant et tension tête bêche : u=+R.i ; u=+L.di/dt ; i=+C.du/dt

et comme dit LPFR, de réfléchir.

exactement il faut juste choisir les conventions et appliquer les loi mercii

[invite5a48ffd1]

juste une petite question : dans un montage que voulez vous dire avec là ou le potentiel élevé?

La pointe de la flèche indique le potentiel le plus élevé.
VA-VB avec VA>VB et la pointe de la flèche en A.

[invite06ca88e4]

La pointe de la flèche indique le potentiel le plus élevé.
VA-VB avec VA>VB et la pointe de la flèche en A.

ah oui merciii chtulhu