Bonjour à tous,
Dans le cadre d'un développement d'un petit jeux vidéo amateur, je cherche à déterminer l’excentricité d'une ellipse formé par la trajectoire d'un objet 1 (vaisseau de masse nul) autour d'un objet 2 (planète) suivant des règle d’attraction gravitationnelle quadratique (F2/1 = u/d²), le tout dans un repère en 2 dimensions.
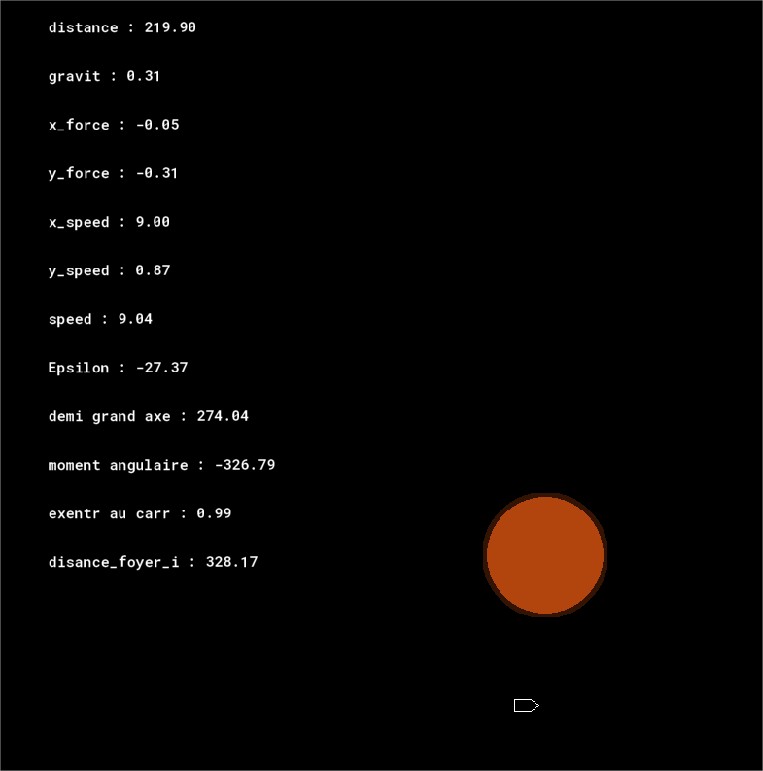
A l'heure actuel je connais :
- la position instantanée de mes deux objets, sachant que l'objet 2 est fixe dans mon repère xy
- donc la distance de l'objet 1 par rapport à l'objet 2 d
- la vitesse instantanée de mon objet 1 par rapport à mon objet 2, V2/1
- le paramètre gravitationnel défini arbitrairement u
- la force d'attraction F2/1 = u/d²
- l'énergie orbital spécifique E = (V2/1)²/2 - u/d (constante)
- le demi grand axe de l'ellipse a = -u/(2E)
Et je cherche à obtenir l'excentricité "e" OU la distance entre les deux foyers "c" (la planète étant l'un d'entre eux) OU le demi petit axe "b" OU la distance entre le foyer et le periapside. Il me semble que la résolution d'un de ces trois paramètres me permettrait d'en déduire les coordonnées de l'ellipse que je souhaite afficher à l'écran.
J'ai exploré la piste du moment cinétique spécifique mais j'ai été bloqué car je ne connais pas l'angle entre mon axe a (demi grand axe) et mon repère xy, ce qui m’empêche d'effectuer un changement de repère.
J'ai aussi essayé de résoudre le problème géométriquement en utilisant la "définition bifocale de l'ellipse" mais je n'ai rien pu déterminer de pertinent :'-(
Je joint une petite capture d'écran afin de faciliter la compréhension :
Je sais que ce n'est pas très beau en l'état actuel, mais la création de sprite sera une étape ultérieur.
J'ai essayé d'être le plus clair possible, si vous avez des idées/remarques/suggestions ou même solutions, je suis preneur
Merci d'avance
-----