Relativité de la simultanéité

[Zefram Cochrane]

Salut,

En mécanique classique, il faut dire "changement de référentiel inertiel". Maintenant, est-ce que Rindler par exemple considère que le jumeau accéléré change de système de datation, donc de référentiel ?

D'après le principe de Wolfgang Rindler : * «*Un observateur accéléré fait les même mesures locales de durées et de distances qu’un observateur inertiel momentanément comobile avec lui.*» ;si je suis stationnaire au centre d'un cercle, peut importe l'amplitude ou la direction de l'accélération, je verrai toujours un cercle.
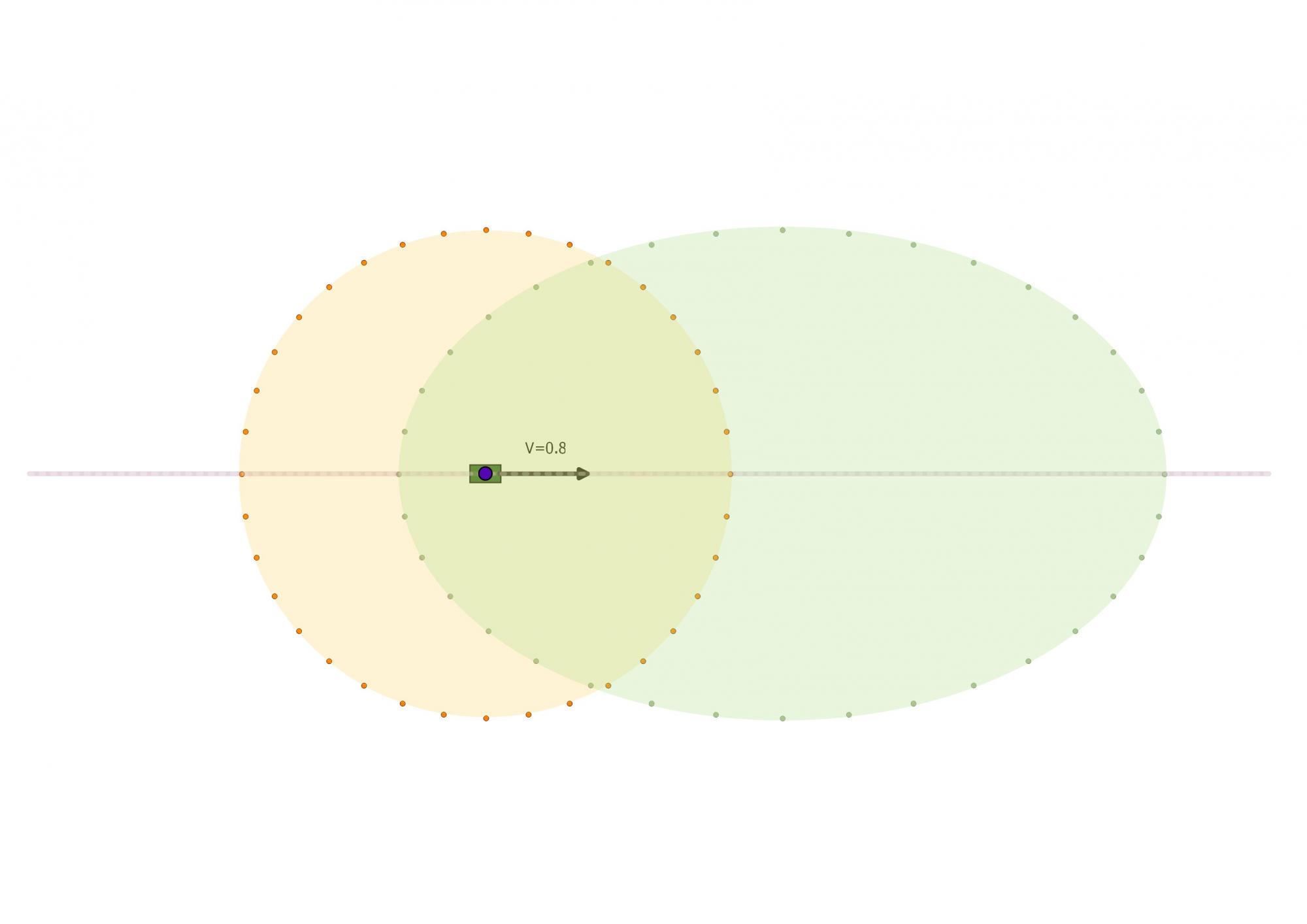
Maintenant, si tu passes à V=0.6c à mon niveau; peu importe l'amplitude ou la direction dans laquelle tu accélère, tu verras la même chose qu'un observateur comobile inertiel passant à V=0.6c à mon niveau.
Ta perspecive du cercle dépend uniquement de ta vitesse relative (amplitude et direction) par rapport à moi.


J'aurais pu également faire figurer le coefficient Doppler de chaque point puisque pour toi, c'est le rapport entre la distance apparente de ce point pour toi et la distance a^pparente de ce point pour moi.

Donc oui, Rindler intègre le changement de référentiel.
edit avec mach3
-----

[Amanuensis]

En mécanique classique, il faut dire "changement de référentiel inertiel".

Jamais vu ça (le il faut) en mécanique classique, ou je m'en souviens plus. Et l'expression est rare (au mieux) au sens d'un demi-tour. Par contre, vu un peu partout dans les présentations vulgarisées de la RR, en particulier pour tous les «exercices de pensée élémentaires» qui forment une grosse partie de cette littérature. Les problèmes équivalents des jumeaux, des trains, quais, tunnels, granges, que sais-je, ne se posent même pas en mécanique classique.

(Dans la même comparaison, d'un côté on voit partout «transformation de Lorentz»), alors que de l'autre on ne ne voit pas souvent «transformation de Galilée», et il n'est pas clair que l'expression soit comprise. Bref, les deux modèles cinématiques, classiques et RR, sont présentés très très différemment, et s'il y a bien des concepts analogues, les discours ne le sont pas du tout. Quel est l'analogue de la métrique en classique? Quand apparaît-il dans les textes cinématiques? Quels sont les analogues des lois de Newton? Quand sont-ils cités dans les textes sur la dynamique en RR? Etc.)

[LLphy]

Quand je dis n'importe quel bouquin, c'est façon de parler, je lis ceci et c'est vraiment très bien amené, l'approche est historique, il reprend les expériences de mesures de la vitesse de la lumière dans l'eau en mouvement, il étudie la réflexion par les miroirs en mouvement dans l'expérience de Michelson et Morley, etc. Après, ça ne m'empêche pas de ne pas avoir encore compris certains points.

https://www.amazon.fr/Relativit%C3%A.../dp/2711770990

[Amanuensis]

Chacun a son bouquin ou texte de vulgarisation fétiche (et maintenant vidéo trouvée sur tel site), qu'il présente comme la perle qui lui a permis de comprendre la RR.

(Au passage l'approche historique est parfaitement adaptée à comprendre l'histoire. En particulier comment des savants très intelligents mais totalement ignorants de la RG se sont creusé la tête, et comment ils ont fait, pour rendre compte des observations des expérimentateurs.)

[Merlin95]

a un moment donné oui, mais pas le même référentiel entre 2 moments différents ...donc il n'y a pas de référentiel unique permettant de dire qu'on peut calculer le "dt'0" comme disait Merlin.

Ca me montre que la relativité générale semble bien donc bien plus complexe que la relativité restreinte.

[viiksu]

je ne comprends pas ces histoires de référentiels: Dans tous les cas si je défini arbitrairement un référentiel fixe par exemple le pied de la tour Eiffel et une horloge attachée sur la tour et que je bouge par rapport à celui-ci que ce soit à pied, à cheval en voiture ou en fusée en revenant au pied de la tour les deux horloges auront divergé cela a été mesuré dans un avion et concernant les satellites GPS on connait parfaitement le décalage journalier de quelque µs.

[viiksu]

Bien entendu quand il y a accélération donc changement de vitesse donc de référentiel le calcul doit se complexifier mais je pense que le principe reste le même non?

[Amanuensis]

Ca me montre que la relativité générale semble bien donc bien plus complexe que la relativité restreinte.

Du point de vue calculatoire et bagage mathématique pour suivre ces calculs, c'est indubitable.

Du point de vue conceptuel, c'est plus subtil. Déjà, c'est nécessairement le cas puisque la RR ne couvre pas la gravitation alors que la RG le fait tout en couvrant tout ce que couvre la RR. Difficile de s'attendre à ce que ce soit moins complexe au sens quantité de concepts. Mais n'est-ce pas alors des évidences? Peut-on faire un peu plus intéressant dans la comparaison?

[Amanuensis]

Un autre point, très important. La RR traite d'un modèle à très forte symétrie, symétrie posée comme postulat. (Et permise par l'absence de gravitation, ce qui n'est pas réaliste.)

Dans les avantages d'une forte symétrie sont évidents des calculs plus simples et une conceptualisation plus limitée.

Certes l'étude détaillée du triangle équilatéral en géométrie est moins complexe que celle du triangle en général. Mais est-ce bien pertinent? Quel est l'intérêt d'une compréhension en profondeur du triangle équilatéral si le cadre est le triangle, et non la symétrie elle-même? (Le triangle équilatéral est une excellente approche pour étudier le groupe de symétrie D3...)

L'analogie est pour dire qu'une partie importante des concepts de la RR concerne la forte symétrie de l'espace-temps de Minkowski (la symétrie est le groupe de Poincaré), et non l'espace-temps en général (du point de vue symétrie, seul le groupe ponctuel, le groupe de Lorentz, reste pertinent).

[Merlin95]

Je ne sais pas avec les dernières remarques de Archi3, j'avoue être au bout de mes "repères" et ne plus avoir de mots.
Car en gros, ce que j'ai compris de ce que dit Archi3 c'est que dans la situation où on est dans deux référentiels non inertiels on ne peut plus définir le temps vu par chacun des observateurs comme cela peut se faire en RR (est-ce bien cela ce que revient à dire Archi3 ?). Du coup, quelque part, on peut moins dire de choses entre les deux observateurs (en tout cas pas ce que la RR pouvait nous dire par les TL). Peut-être est-ce pour cela que l'on doit introduire des informations émises dans un référentiel et réceptionnées dans un autre, et c'est seulement cela qui a une réalité physique ? Je vois cela comme un changement de paradigme difficile à accepter, et c'est de ce point de vue que la RG me semble plus compliquée que la RR.

[Amanuensis]

dans la situation où on est dans deux référentiels non inertiels on ne peut plus définir le temps vu par chacun des observateurs

Je ne sais pas répondre à des questions avec «être dans deux référentiels non inertiels».

Cela utilise des concepts inadaptés, et cela demande du temps pour essayer de comprendre même de quoi il est question.

1) Définir un référentiel non inertiel est souvent très difficile, alors que dans la majorité des cas on n'a besoin que du fait qu'un mouvement n'est pas inertiel. (La confusion entre les deux ne pose pas de pb en RR, car à un mouvement inertiel correspond un et un seul référentiel inertiel.)

2) La seule notion fondamentale de temps est le temps propre, et cela s'applique à tout mouvement (mais pas à des référentiels généraux). On peut toujours parler en terme de temps propre sans s'occuper de «temps coordonnée» ou de «temps d'un référentiel inertiel». (A contrario, à chaque référentiel inertiel on peut associer «canoniquement» un «temps», en fait une coordonnée temporelle sur l'espace-temps, c'est à dire une relation de simultanéité. Alors qu'un temps propre n'est pas une relation de simultanéité.)

3) Ce qu'on introduit n'est pas «ce qui est émis/reçu dans un référentiel», mais ce qui est émis/reçu par un émetteur ou récepteur qui suit un mouvement accéléré. Comme on ne parle que de mouvements (et non de référentiels) ce qui est pertinent et utilisable est les temps propres (de l'émetteur, du récepteur).

Le temps propre ne pose pas de débat sur son «caractère physique» (au sens de la discussion présente). De même, ce qui émis ou reçu.

Je vois cela comme un changement de paradigme difficile à accepter, et c'est de ce point de vue que la RG me semble plus compliquée que la RR.

Certes. Mais le «paradigme» de la RR n'a pas de nécessité. Parler directement en termes de mouvements (ligne d'Univers), de temps propre, d'observations de signaux, marche pour résoudre (comprendre) plein d'aspects de la RR, et fournissent un cadre dans lequel on peut présenter aisément les concepts spécifiques de référentiel inertiel, de temps de référentiel inertiel, de TL. Et la première liste de concepts passe facilement à la RG!

Je comprends ce que vous indiquez comme une phénomène déjà bien constaté, qu'a déjà d'ailleurs cité mach3: le paradigme spécifique de la RR rend l'abord de la RG plus difficile, et fait peut-être paraître la RG comme «plus compliquée», au delà des causes intrinsèques d'une plus grande complexité.

Le dilemme pour la pédagogie est là: doit-on privilégier un «paradigme» simple mais partiellement une impasse (donc adapté à ceux qui ne cherche pas à aller plus loin, à terme, que la RR) ; une un paradigme apparemment(1) plus compliqué, mais préparant bien à une progression plus loin?

[Facile de voir que ma position dans ce dilemme est en faveur de la seconde approche. Biais à prendre en compte. Ce qui ne m'empêche pas de voir les avantages de la première, et de l'appliquer quand nécessaire.]

(1) Apparemment, car si on prend les concepts profonds, ce que j'appelle la «philosophie du temps et de l'espace», cela ne me paraît pas plus compliqué, et d'ailleurs l'obstacle principal n'est pas tant la RR que l'insuffisante compréhension conceptuelle de la mécanique classique, ne serait-ce que le concept de relativité galiléenne (et donc la notion de lieu, d'espace). (Point aussi mentionné, par Archi3 au moins.) Ou de référentiel non galiléen, ou de pesanteur, etc. Pour moi la meilleure approche encore est de faire bien comprendre les concepts de la mécanique classique, mais cela ne convient à personne, la préférence est toujours de se jeter sur la RR, quelle que soit la solidité de l'assise conceptuelle concernant la mécanique classique...

[Merlin95]

On peut toujours parler en terme de temps propre sans s'occuper de «temps coordonnée» ou de «temps d'un référentiel inertiel». (A contrario, à chaque référentiel inertiel on peut associer «canoniquement» un «temps», en fait une coordonnée temporelle sur l'espace-temps, c'est à dire une relation de simultanéité. Alors qu'un temps propre n'est pas une relation de simultanéité.)

Dans le cadre de mouvements accélérés, il n'est donc pas possible de parler de temps coordonnées, c'est-à-dire de définir une relation de simultanéité ? ou est-ce juste difficile et/ou encore contraire à l'esprit de la RG qui a passé la relation de simultanéité au second plan ?

[Merlin95]

Une autre possibilité, c'est que c'est peut-être possible (et difficile) et "artificiel".

Ainsi, quand vous dîtes :

On peut toujours parler en terme de temps propre sans s'occuper de «temps coordonnée»

Par exemple, imaginons deux mouvements accélérés complètement quelconques, et puis au bout d'un moment, ils se rencontrent.
Le moment de leur début d'existence (évènement) n'ont pas besoin d'être comparé l'un à l'autre pour comparer leur temps propre. Ce temps propre est juste définit par leur chemin dans l'espace temps.

[Archi3]

Dans le cadre de mouvements accélérés, il n'est donc pas possible de parler de temps coordonnées, c'est-à-dire de définir une relation de simultanéité ? ou est-ce juste difficile et/ou encore contraire à l'esprit de la RG qui a passé la relation de simultanéité au second plan ?

tu progresses . C'est tout à fait possible de définir des temps coordonnées dans (une infinité) de référentiels non galiléens (dont certains peuvent etre tels que l'observateur accéléré soit "immobile" (à coordonnées constantes) dans ce référentiel, mais il y en a aussi une infinité de différents). Ce qui n'est plus possible (contrairement aux réf. galiléens), c'est de synchroniser ces temps, c'est à dire de définir une relation d'équivalence "est simultané avec" (qui soit comme toute bonne relation d'équivalence réflexive, symétrique et transitive), qui permette de définir des classes d'équivalences d'événements simultanés entre eux dans ce référentiel. Ce n'est possible QUE dans les référentiels galiléens, dans lesquels SEULS les observateurs inertiels (à accélération propre nulle) peuvent etre (éventuellement) immobiles ou voyagent à vitesse constante.
Dans la mesure où la simultanéité n'est plus définissable, il n'est plus possible de dire , pour deux évènement A et B dont l'intervalle est du genre temps , et donc séparés par un temps propre ∆To , quels sont les évènements simultanés avec eux pour l'observateur accéléré, et d'évaluer le temps ∆T'o "pour cet observateur" . Ce n'est possible que si l'observateur est inertiel (d'ou le fait qu'en RR on ne fasse les calculs "que dans les référentiels galiléens") .

[Archi3]

Remarque : la propriété est analogue en RG : la simultanéité "globale" ne peut etre définie aussi que dans certains référentiels particuliers . Mais ils sont plus compliqués à définir en RG, et en général ils n'auront pas les mêmes propriétés qu'en RR : par exemple ils ne seront pas statiques (la distance entre les observateurs "immobiles" dans ce référentiel peut varier au cours du temps, c'est le cas du référentiel cosmologique en co-mouvement), ou bien l'écoulement de temps propre entre deux évènements "simultanés" ne sera pas le même ,( c'est le cas d'un champ de gravitation réel statique), ou encore la métrique spatiale n'est pas euclidienne (cas de l'univers stationnaire d'Einstein avec constante cosmologique par exemple).

[Archi3]

Une autre possibilité, c'est que c'est peut-être possible (et difficile) et "artificiel".

Ainsi, quand vous dîtes :


Par exemple, imaginons deux mouvements accélérés complètement quelconques, et puis au bout d'un moment, ils se rencontrent.
Le moment de leur début d'existence (évènement) n'ont pas besoin d'être comparé l'un à l'autre pour comparer leur temps propre. Ce temps propre est juste définit par leur chemin dans l'espace temps.

exact, mais dans ce cas tu ne peux pas dire si le début des mouvements sont simultanés entre eux , ce qui fait perdre tout intérêt à la comparaison des temps propres (ce ne serait pas étonnant en mécanique classique que les temps écoulés soient différents si le début n'a pas lieu en même temps, quand tu vas chercher des copains à la gare près de chez toi, tu ne t'étonnes pas d'avoir passé moins de temps dans ta voiture que eux dans le train ).
Le "paradoxe" n'existe que si le début et la fin sont simultanés - mais en présence d'accélération, ceci n'est définissable que si en fait ils ont lieu en même temps ET AU MEME ENDROIT (donc en fait sont un seul évènement ) , d'où la formulation du paradoxe de Langevin, où il est indispensable que les jumeaux soient ensemble à la fois au début et à la fin (ce qui n'est possible que si l'un au moins n'est pas inertiel).

[Amanuensis]

Dans le cadre de mouvements accélérés, il n'est donc pas possible de parler de temps coordonnées,

Si bien sûr, et c'est bien utile. Un temps coordonnée, c'est juste attribuer à chaque événement une date, une coordonnée temporelle (d'où le nom de temps-coordonnée). C'est la notion de coordonnée au sens usuel, comme associer à chaque point du plan une paire de réels. Dans le cas de l'espace-temps on est en quatre dimensions, quatre coordonnées et on peut définir (à partir de la métrique) la notion de coordonnée temporelle, de temps-coordonnée.

On peut le faire d'une infinité de manières, la seule contrainte est posée par le respect de l'ordre causal (cela s'exprime plus rigoureusement avec la métrique). Le problème est qu'un temps coordonnée quelconque n'a pas beaucoup des propriétés autre, et en particulier pas celles qu'on en attend quand on pense «temps» au sens de la mécanique classique.

Pour un observateur accéléré (une ligne d'univers quelconque), on peut toujours choisir un temps-coordonnée (je vais dire une datation, donner à chaque événement un réel qui représente une «date») qui coïncide avec son temps propre (qui est une datation particulière propre à l'observateur, à une ligne d'univers). Mais ne serait-ce que trouver une datation qui coïncide aussi bien avec le temps propre d'un observateur et celui d'un autre quasiment jamais possible, (1) même pas en RR, s'ils se rencontrent seulement deux fois (deux lignes d'univers s'intersectant deux fois): c'est essentiellement ce qu'illustre le paradoxe des jumeaux.

(1) C'est possible par exemple quand les deux lignes sont symétrique l'une de l'autre par une symétrie de l'espace-temps, qu'elles s'intersectent ou pas. (Et c'est pourquoi la symétrie d'un espace-temps est si importante, et qu'on trouver des datations avec de bonnes propriétés dans le très symétrique espace-temps de Minkowski)

c'est-à-dire de définir une relation de simultanéité ?

Question de définition. Si on dit que la notion de simultanéité ne s'applique qu'en classique et pour les référentiels inertiels de la RR, non, par définition.

Si on dit qu'une relation de simultanéité est une relation définie par une datation, à savoir «avoir la même date», un temps-coordonnée définit une simultanéité, par définition.

Si on accepte d'appliquer le terme «simultanéité» seulement pour des datations ayant certaines propriétés, cela va dépendre de quelles propriétés on parle, et l'existence d'une telle simultanéité dépendra des propriété du modèle d'espace-temps considéré.

Le point essentiel est qu'une datation quelconque n'a pas les propriétés qu'on attend intuitivement d'une simultanéité, seuls le temps de la mécanique classique l'a; et les temps-coordonnées «canoniques» définis pour les référentiels inertiel en RR les ont presque.

Il est d'ailleurs très intéressant de se pencher sur ces propriétés, et sur les différents cas de datation classées selon la partie de ces propriétés qui sont conservées. (Le message #255 en donne quelques exemples.)

ou est-ce juste difficile et/ou encore contraire à l'esprit de la RG qui a passé la relation de simultanéité au second plan ?

Au contraire, c'est très facile de définir un temps-coordonnée, puisque c'est très peu contraint. Le problème, encore une fois, est que cela n'a que rarement tout ou partie des propriétés intuitives que l'on prête au terme «simultanéité».

Parce que justement un temps-coordonnée est arbitraire, il n'a pas de sens physique (autre que le respect de l'ordre causal, un ordre partiel), et conceptuellement passe au second plan. Une coordonnée temporelle devient juste utile pour un repérage et pour les calculs, de même que les coordonnées cartésiennes d'un plan sont utiles pour les calculs ou le repérage. On peut se balader en forêt sans s'intéresser aux longitude et latitude ou aux coordonnées Lambert, mais elles sont utiles si on utilise un plan , établir un rendez-vous, (repérage) et pour faire des calculs.

[Dans ce texte j'ai utilisé quelques-uns des concepts présentés plus usuellement en RG. Lesquels ont posé des difficulté de compréhension?]

[Archi3]

Si on dit qu'une relation de simultanéité est une relation définie par une datation, à savoir «avoir la même date», un temps-coordonnée définit une simultanéité, par définition.

à ma connaissance, cependant, personne n'adopte cette définition de la simultanéité, qui n'obéit à aucune propriété habituellement associée a la simultanéité. Par exemple si on adopte comme temps-coordonnée l'heure solaire locale, il faudrait considérer comme simultané les moments ayant la même heure locale (midi à Paris serait simultané avec midi à New York), alors que ces évènements sont dans le cone de lumière l'un de l'autre, ce qui entraine par exemple qu'on pourrait avoir des informations sur un évènement simultané avec A avant que A ne se produise !

dans la définition d'E-P, ce ne sont jamais les "mêmes temps t" qui sont simultanés par principe (sauf dans le cas précis où on a pu définir une simultanéité et associer une coordonnée t à chaque classe d'équivalence , ce qui pour répéter n'est possible QUE dans certains référentiels très particuliers) : c'est une opération de synchronisation qui calcule un décalage horaire entre les différents temps pour savoir comment ils sont synchronisés. Malheureusement dans un référentiel quelconque, cette opération n'est pas transitive et on aboutit au paradoxe qu'un évènement peut ne pas etre synchronisé avec lui même ...

[Amanuensis]

[Edit: le texte m'a pris 1/2 heure à écrire et relire, il ne prend pas en compte le message précédent. Mais il y répond quand même, le texte ci-après étant une synthèse cherchant à prendre en compte les différents points de vue, même si la conclusion ne le fait pas.]

Aparté philosophique (mais totalement dans le sujet tel que donné par le titre)

Le terme simultanéité pose problème.

D'un côté, il a un sens clair dans la vie de tous les jours, et il ne pose aucun problème en mécanique classique (au contraire, c'en est un postulat essentiel, celui du temps absolu, équivalent à dire «il existe une relation absolue de simultanéité», c'est la relation «être simultanés» entre deux événements est absolue).

De l'autre, le mieux qu'on peut en faire dans le cas général d'un espace-temps modélisé dans le cadre de la relativité générale, c'est à dire la théorie scientifique dominante pour des modèles d'espace-temps rendant compte de la «réalité», est artificiel (un temps-coordonnée quelconque) et n'a que très peu des propriétés «intuitivement attendues» (il a quand même la principale, l'essentielle, celle qui est derrière le mot temps, le respect de l'ordre causal).

Que faire devant ce constat?

Une possibilité radicale est d'abandonner le concept, ou plutôt le garder là, et seulement là, où il ne pose aucun problème: dans le cadre de l'approximation somme toute très utile qu'est la mécanique classique. Pour la plupart des humains sur Terre c'est adapté, et largement suffisant.

Le problème ne se pose que pour les physiciens, quelques ingénieurs (qui ont besoin d'une précision meilleure que celle de la mécanique classique) ; quelques philosophes s'intéressant aux concepts de temps et d'espace; et les curieux cherchant à comprendre ce que racontent ces physiciens et philosophes, et comment travaillent ces ingénieurs (donc comment on calcule).

Le constat qu'un temps-coordonnée quelconque, la seule possibilité résiduelle de sauver une notion de simultanéité dans tous les cas (en particulier pour l'univers tel qu'on l'observe!), n'a pas de sens physique est troublant.

Cela ,e s'améliore pas quand on rajoute le constat que dans le meilleurs des cas particuliers, le temps-coordonnée canonique des référentiels inertiels de l'espace-temps de Minkowski, on n'a pas toutes les propriétés qu'on voudrait, impossibilité illustrée par le paradoxe des jumeaux. On peut sérieusement se poser la question si la notion même de simultanéité a un quelconque sens physique.

La simultanéité en RR est basée sur une procédure physique, concrète, la synchronisation d'Einstein-Poincaré. Elle ne fonctionne que dans des cas très particuliers, entre deux observateurs inertiels et «parallèles», au sens où la durée (propre) d'un échange aller-retour de signaux lumineux est invariante.

On peut voir cela de deux manières: soit comme «physique» (au sens de non artificiel, après tout c'est une procédure expérimentale bien définie), soit comme une méthode pour définir un temps-coordonnée ayant des propriétés intéressantes (dont une est d'avoir une procédure physique pour l'établir!).

C'est aussi un constat aisé que le choix d'un référentiel inertiel et de la datation canonique correspondante simplifie énormément les calculs en RR (calculs en coordonnées) ; et permet ainsi des calculs ne demandant pas de mathématiques trop compliquées, des exemples numériques, des exercices, tous bien utile pour une pédagogie visant à faire comprendre quelques concepts (mais dont beaucoup spécifiques à la RR). Il y a bien d'autres approches, dont des calculs symboliques en 4D, mais cela demande des outils abstraits (mathématiques) au-delà du «pas trop compliqué».

Une autre «propriété intéressante» (une source de confusion, selon un autre point de vue) est la relation univoque entre vitesse (quadri-vitesse pour être rigoureux, une vitesse étant relative, mais une quadrivitesse non), MRU (ou mouvement inertiel) au sein de ceux passant par un même événement, référentiel inertiel et relation de simultanéité. Cela permet les «raccourcis» consistant à parler du référentiel d'un MRU, et même carrément du référentiel d'un observateur, le référentiel défini par sa quadri-vitesse instantanée, et de là «changer de référentiel» pour parler d'un changement de quadri-vitesse (ce qui n'arrive jamais, par définition, pour un mouvement inertiel!). Et aussi de *«vu d'un observateur» pour parler de simultanéité temporelle (et non pas de ce qu'il voit au sens propre). C'est cette chaîne de bi-univocité qui amène à la notion de «relativité de la simultanéité».

Mais est-ce que cet ensemble de propriétés intéressantes font d'une relation de simultanéité dérivant d'un référentiel inertiel quelque chose de «physique», de «non artificiel», un concept fondamental à la physique? Le domaine d'application est si restreint qu'on peut en douter. La physique n'est pas un domaine où on privilégie couramment les cas particuliers aux cas généraux.

À l'opposé, si on se tourne vers les pratiques de la RG, on constate que le terme de simultanéité n'est utilisé que dans des cas très particuliers (liée à une forte symétrie de l'espace-temps considéré). La définition générale selon laquelle le terme pourrait se substituer à «coordonnée temporelle» n'est pas vraiment utilisée: le terme n'apporte que des ambiguïté, autant, puisque suffisant, parler de coordonnée temporelle (ou temps-coordonnée pour s'opposer à «temps propre», terme qui ne peut pas véhiculer le sens de simultanéité --mais qui garde la propriété essentielle d'ordre causal, et a en plus la propriété d'être compatible avec une unité invariante de durée).

Voilà en gros le faisceau d'arguments pour proposer la solution radicale consistant à abandonner totalement le concept de simultanéité «en relativité», y compris celui de «relativité de la simultanéité», concept qui ne peut s'appliquer qu'à des cas particuliers dans un modèle d'espace-temps particulier.

Bien sûr, ce peut être considéré comme trop radical (comme déjà signalé plusieurs fois) si on ne s'intéresse qu'à la RR, qu'à quelques expériences de pensée illustrant les différences avec la mécanique classique, et qu'aux calculs simples que la RR permet et sur lesquels vont pouvoir s'appuyer les «explications» desdites expériences de pensée.

Mais côté comprendre la théorie principale des physiciens (la RG) ou philosopher sur le temps et l'espace, c'est peut-être strictement nécessaire.

[Archi3]

Quelques remarques sur ce que dit Amanuensis

De l'autre, le mieux qu'on peut en faire dans le cas général d'un espace-temps modélisé dans le cadre de la relativité générale, c'est à dire la théorie scientifique dominante pour des modèles d'espace-temps rendant compte de la «réalité», est artificiel (un temps-coordonnée quelconque) et n'a que très peu des propriétés «intuitivement attendues» (il a quand même la principale, l'essentielle, celle qui est derrière le mot temps, le respect de l'ordre causal).

le respect de l'ordre causal "local" (pour un observateur donné) est plutot assuré par le choix d'une coordonnée "vraiment" temporelle au sens où rien de ce que ne fait un observateur à un temps to ne peut influencer le passé de cet observateur, à t <to : ceci ne fait aucunement référence à la notion de simultanéité et est valable de toutes façons dans tous les référentiels, qu'ils soient synchronisables ou pas. Si tu veux rajouter une notion de simultanéité qui ajoute un critère de plus, il me semble indispensable que cette notion rajoute aussi un critère d'ordre causal non local : c'est à dire que ce que fait un observateur à un instant t ne peut pas influencer ce qui arrive à un autre observateur à un temps inférieur au temps t'o considéré comme simultané avec to (t'<t'o) sachant qu'il n'est pas exigé que to = t'o, mais simplement que ces temps soient liés par le critère de simultanéité (exemple du décalage horaire ordinaire).

Or ce critère n'est pas vérifié pour une définition de la simultanéité par to=t'o, justement ...

Et je ne suis pas sur qu'il soit vérifié systématiquement pour une autre procédure que E-P, qui serait donc la seule possible qui conserve cette propriété (conjecture à vérifier).

Voilà en gros le faisceau d'arguments pour proposer la solution radicale consistant à abandonner totalement le concept de simultanéité «en relativité», y compris celui de «relativité de la simultanéité», concept qui ne peut s'appliquer qu'à des cas particuliers dans un modèle d'espace-temps particulier.

Bien sûr, ce peut être considéré comme trop radical (comme déjà signalé plusieurs fois) si on ne s'intéresse qu'à la RR, qu'à quelques expériences de pensée illustrant les différences avec la mécanique classique, et qu'aux calculs simples que la RR permet et sur lesquels vont pouvoir s'appuyer les «explications» desdites expériences de pensée.

Mais côté comprendre la théorie principale des physiciens (la RG) ou philosopher sur le temps et l'espace, c'est peut-être strictement nécessaire.

mais concrètement, je suppose que tu ne proposes pas d'abandonner complètement l'estimation des "âges" des galaxies qu'on voit dans les télescopes ou d'interdire la publication des décalages horaires entre les pays ? il me semble évident que la notion de simultanéité est partout présente dans notre conception du monde, et qu'il me parait plus réaliste d'en examiner les limites (et les raisons pour lesquelles elle rencontre des limites) que de "l'abandonner totalement" - ce qui a mon avis devient totalement incompréhensible à ceux qui n'ont pas fait le centième du cheminement intellectuel que tu as fait.

[Paradigm]

Bonjour à tous,

(il a quand même la principale, l'essentielle, celle qui est derrière le mot temps, le respect de l'ordre causal).

L'ordre causal qui correspond à une relation d'ordre partiel entre les événements constituants l'espace-temps est-il aussi temporel ? C'est à dire peut-on définir entre deux événements quelconques ayant une relation de causalité, mais appartenant à des lignes d'univers distinctes, une durée univoque ?

Cordialement,

[Archi3]

Bonjour à tous,



L'ordre causal qui correspond à une relation d'ordre partiel entre les événements constituants l'espace-temps est-il aussi temporel ? C'est à dire peut-on définir entre deux événements quelconques ayant une relation de causalité, mais appartenant à des lignes d'univers distinctes, une durée univoque ?

Cordialement,

deja par définition, si ils ont une relation de causalité, c'est qu'il y a des lignes d'univers de genre lumière ou temps (mais pas espace) les connectant (sinon ça reviendrait à dire qu'une influence peut se propager plus vite que la lumière ... ) . Mais la durée (temps propre ) mesurée le long de ces lignes n'est nullement constante bien sur. En revanche il existe une ligne de plus grande durée propre (qui est précisément une géodésique de l'espace temps, c'est à dire le trajet d'une particule (éventuellement photon) en chute libre les connectant) - en RR c'est simplement le trajet d'un observateur inertiel les connectant, c'est à dire la ligne x,y,z = constante dans le référentiel galiléen où ils ont lieu au même endroit, si l'intervalle est du genre temps, ou le trajet du photon les connectant si il est du genre lumière.

[Paradigm]

Mais la durée (temps propre ) mesurée le long de ces lignes n'est nullement constante bien sur.

On peut les connectés par une infinité de ligne d'univers de genre temps ou lumière, mais les durées propres (intervalle spatio-temporel entre les deux événements) de ces lignes d'univers ne seront pas forcement égales entre elles si ?

[Amanuensis]

L'ordre causal qui correspond à une relation d'ordre partiel entre les événements constituants l'espace-temps est-il aussi temporel ? C'est à dire peut-on définir entre deux événements quelconques ayant une relation de causalité, mais appartenant à des lignes d'univers distinctes, une durée univoque ?

Non. C'est juste un ordre partiel, sans information «métrique» au sens étroit, c'est à dire sur les valeurs des durées (ou des distances, pareil).

(Cela permet les «théories conformes», par exemple, où l'ordre causal reste dans l'arrière-plan (la métrique est localement minkowskienne), mais on ne «connecte» pas les échelles spatio-temporelles locales, on se retrouve avec un champ scalaire pour mathématiser les échelles, et une métrique pouvant prendre la forme a²(t, X) (dt²-dX²). la notion de «temps» au sens de l'ordre causal partiel est conservée. Pas eu beaucoup de succès, il me semble.)

[Amanuensis]

On peut les connectés par une infinité de ligne d'univers de genre temps ou lumière, mais les durées propres (intervalle spatio-temporel entre les deux événements) de ces lignes d'univers ne seront pas forcement égales entre elles si ?

Quand on peut exhiber une telle connexion, on parle exactement de synchronisation! Et si cela concerne tout l'espace-temps on a une synchronisation globale.

(Mais possible que je n'ai pas compris de quelle connexion il s'agit.)

Ce sont des cas très particuliers (encore une forte symétrie d'espace-temps...), un exemple hors RR étant le temps cosmique (métrique FLRW): le temps propre entre (t1, X) et (t2, X) le long du chemin t -> (t, X) est indépendant de X (indépendant du lieu, au sens défini par le référentiel comobile). Mais ce n'est pas le cas des coordonnées de Schwarzschild dans la géométrie (externe) du même. (Cf. un message d'Archi3 ce matin.)

[Paradigm]

Quand on peut exhiber une telle connexion, on parle exactement de synchronisation!
(Mais possible que je n'ai pas compris de quelle connexion il s'agit.)

"Connexion" : Un signal reliant les deux événements qui peut servir pourquoi pas à modifier l'heure du récepteur (date d'émission + durée propre du trajet). Si on représente l'espace-temps par une variété différentielle comment se représente une géodésique reliant deux événements ? Cela n'utilise pas la notion de connexions affines ?

[Paradigm]

(Cela permet les «théories conformes», par exemple, où l'ordre causal reste dans l'arrière-plan (la métrique est localement minkowskienne), mais on ne «connecte» pas les échelles spatio-temporelles locales.)

C'est en lien avec la notion de "structure conforme" dont parle Marc Lachièze-Rey ?

[Amanuensis]

"Connexion" : Un signal reliant les deux événements qui peut servir pourquoi pas à modifier l'heure du récepteur (date d'émission + durée propre du trajet). Si on représente l'espace-temps par une variété différentielle comment se représente une géodésique reliant deux événements ? Cela n'utilise pas la notion de connexions affines ?

Le modèle mathématique est celui présentant un référentiel comme un ensemble de lignes d'Univers partitionnant l'espace-temps (ou un ouvert de ...), et l'espace-temps comme un fibré de base 3D des «lieux», et comme fibre une ligne d'Univers . Une connexion d'un tel fibré est bien une manière de faire correspondre les lignes infinitésimalement proches, ce qui peut être utilisé pour en correspondance les temps propres. Mais la correspondance peut être n'importe quoi, les seules contraintes sont la dérivabilité (ou mieux, Cinfini) et une dérivée strictement monotone.

C'est bien à ce sens là que j'avais répondu.

Choisir une connexion sur un référentiel vu comme fibré, c'est un peu plus faible que choisir une datation. Une datation définit une connexion, mais si on note t(P) cette datation (une fonction des événements vers les réels) alors la datation f(t(P)), avec f strictement monotone (typiquement croissante) définit la même connexion. La connexion capture la simultanéité au sens «égalité de date», puisque la fonction f ne change pas cette égalité. D'où l'idée que cette connexion mathématise une synchronisation.

Note : tout cela n'est valide que pour des espaces-temps «raisonnables», pas de boucle temporelle par exemple.

(1) L'adjectif affine peut être trompeur, en particulier si on pense qu'il a une relation avec le terme «paramètre affine» pour le temps propre. (La connexion sur un référentiel n'est pas contrainte en relation avec les temps propre. On peut d'ailleurs en parler sans métrique, donc nécessairement sans relation avec le temps propre.) La notion de connexion affine signale que c'est une connexion entre espaces vectoriels tangents aux fibres, ici entre dt et dt', et par intégration entre datations. Dans le contexte on peut omettre le «affine».

[Amanuensis]

PS: La connexion affine sur un référentiel vu comme fibré n'a rien à voir avec la connexion affine apparaissant en RG ; cette dernière est sur le fibré vectoriel, le fibré qui a un événement associe l'espace vectoriel 4D tangent. Même concept mathématique, appliqué à deux cas différents.

[Amanuensis]

C'est en lien avec la notion de structure conforme dont parle Marc Lachièze-Rey ?

Oui .