Equation de la chaleur en présence de forts gradients

[Antoane]

Bonjour,

En version courte : l'équation de la chaleur

(avec λ la conductivité, ρ la masse volumique, c_p la chaleur spécifique et S la puissance volumique dissipée)
est-elle valide dans le cas où les gradients (dT/dx et dT/dt) sont grands ?


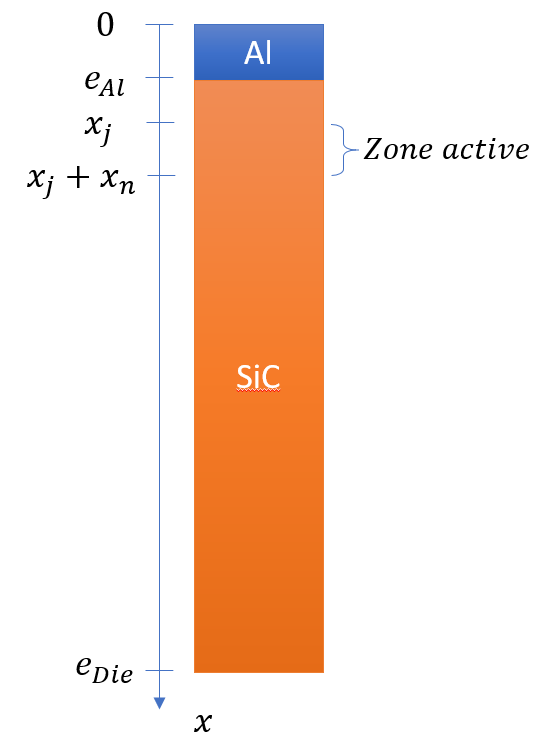
Je m'intéresse à la fiabilité de transistors en régime de court-circuit : on applique quelques centaines de volts aux bornes du composants puis on le rend passant. Un courant de quelques centaines d'ampères y circule alors, ce qui engendre une dissipation de puissance assez phénoménale, de l'ordre de la centaine de kW dans une puce d'une dizaine de mm². Par ailleurs, la majorité de cette puissance est dissipée au sein de la zone active du composant, qui ne mesure que quelques µm d'épaisseur. Le composant ne supporte pas longtemps le traitement et est détruit après une dizaine de µs, alors que l'énergie dissipée est proche de un joule.

Lorsqu'on réalise des simulations (généralement en 1D) par éléments finis de ce genre de dispositifs, en prenant en compte la dépendance des caractéristiques (λ, c_p) des matériaux avec la température, on trouve des températures crêtes au sein du semi-conducteur de l'ordre de 1000 à 1800 K, avec des gradients importants : de l'ordre de 100 MK/s et 50 MK/m.

Dans ces conditions, l'équation de la chaleur "classique" reste-t-elle valable où faut-il l'amender ? Je suis très limité en thermique mais avais discuté rapidement avec quelqu'un réputé compétant qui avait des doutes sur la question.

Merci.
-----

[coussin]

D'un point de vue purement mathématique, une équation différentielle est toujours valable. Quels que soient les magnitudes des gradients.
Après, c'est la résolution numérique qui peut poser problème. Il faut une "grille assez fine" à la fois temporelle et spatiale pour être capable de "résoudre" ces gradients énormes.

[Antoane]

Bonjour et merci pour ta réponse.

Pas de problème pour ce qui est de la résolution numérique.
Je me pose des questions sur la validité physique de l'équation, un peu comme quelqu'un qui se demanderait si son utilisation de la composition de vitesse dans le cadre de la mécanique Newtonienne reste valide lorsque les vitesses sont grandes. Mais c'est peut-être ce que tu entends par "validité mathématique de l'équation différentielle" ?

[coussin]

Je comprends. À ma connaissance, il n'y a pas d'autre "équation de la chaleur" plus générale dont celle-ci serait la forme pour des gradients modérés.
Ceci dit, je ne suis pas spécialiste en ce domaine

[A voir en vidéo sur Futura]

[coussin]

Il y a bien une équation beaucoup plus générale qui est l'équation de transport de Boltzmann (BTE). Mais je ne sais pas si l'équation de la chaleur est un cas limite de BTE ni même s'il y a un lien clair entre les deux.
Attendons les avis des spécialistes

[azizovsky]

Il y'a ce document https://s3.amazonaws.com/academia.ed..._chaleur_a.pdf
et

La loi parabolique de conduction de la chaleur est réputée ne pas pouvoir rendre compte des transferts thermiques instationnaires dans les tout premiers instants du régime transitoire, en raison du caractère “instantané” de la relation qui lie le flux de chaleur au gradient de température dans la loi de Fourier. L'introduction d'un temps de relaxation dans cette relation, qui conduit à l'équation hyperbolique de la chaleur, n'est pas totalement satisfaisante. Hormis les problèmes physiques que cela soulève, une réflexion sur la dimension des espaces concernés par les régimes transitoires ultra rapides montre qu'un problème fondamental se doit d'être envisagé: l'interaction microscopique des porteurs d'énergie du milieu avec la frontière, siège de l'événement thermique. Une modélisation macroscopique du transport de la chaleur à l'échelle du temps de relaxation de ces porteurs et de leur libre parcours moyen est proposée, par le biais de la modification des conditions aux limites. Les apports significatifs de ce modèle sont dégagés à partir d'un exemple d'application: le mur semi-infini soumis à un échelon de température sur sa face

s'il y'a moyen d'avoir accès à
https://www.sciencedirect.com/scienc...90072900011960

[Antoane]

Bonjour,

merci pour vos retours.

Il y a bien une équation beaucoup plus générale qui est l'équation de transport de Boltzmann (BTE). Mais je ne sais pas si l'équation de la chaleur est un cas limite de BTE ni même s'il y a un lien clair entre les deux.

J'espère que ce n'est pas pertinent car sinon je vais galérer

Il y'a ce document https://s3.amazonaws.com/academia.ed..._chaleur_a.pdf

Le lien n'aboutit pas chez moi, en as-tu un autre ?

https://www.sciencedirect.com/scienc...90072900011960

J'y ai accès, si quelqu'un veut (par MP).

J'étudie ça et reviendrai vous voir.

[yvon l]

Pour moi, la montée en température se fait en adiabatique (sans échange de chaleur de la jonction avec l’extérieur). Donc je raisonnerais en considérant l’énergie accumulée dans la jonction au moment du court-circuit.
Si par exemple la source de tension est un condensateur, l’énergie 1/2CV² dans le condensateur va se transformer en énergie thermique dans la jonction. On peut alors connaître la température que cette énergie produit si on connaît le volume et la capacité thermique de la jonction.
Si maintenant la source est classique, cela dépend de sa résistance interne (limitation du courant)… mais cela est une autre histoire...

[Antoane]

Bonjour et meric pour ta réponse,

Pour moi, la montée en température se fait en adiabatique (sans échange de chaleur de la jonction avec l’extérieur). Donc je raisonnerais en considérant l’énergie accumulée dans la jonction au moment du court-circuit.
Si par exemple la source de tension est un condensateur, l’énergie 1/2CV² dans le condensateur va se transformer en énergie thermique dans la jonction. On peut alors connaître la température que cette énergie produit si on connaît le volume et la capacité thermique de la jonction.

Les simulations montrent que la chaleur n'a, en 10 µs, pas le temps de diffuser dans toute la puce : la surface est à ~1500 K tandis que la face arrière (à quelque centaines de µm de là) est encore à une température proche de l'ambiant - d'où le fort dT/dx.

Si maintenant la source est classique, cela dépend de sa résistance interne (limitation du courant)… mais cela est une autre histoire...

Les tests sont normalisés et il s'agit de faire fonctionner le transistor en limitation de courant (i.e. saturé pour un MOSFET par exemple) en maintenant la tension constante à ses bornes. C'est généralement fait avec un banc de condensateurs stockant une énergie très supérieure à celle dissipée au court du test.

[yvon l]

Ceci confirme bien : comportement adiabatique pour calculer la température pendant le courant de pointe, toute l'énergie sert a augmenter la température de la jonction. C'est à cette pointe de température que doit résister la jonction. La puissance est alors pendant ce temps très court (10µs) est énorme (100kW pour 1J à dissiper), mais n'a pas de signification particulière. C'est le volume de la jonction qui déterminera la température atteinte pendant la décharge du condensateur. Difficile à déterminer car elle ne sera pas homogène (géométrie et répartition du courant dans la jonction) - d'où test nécessaire...

[RomVi]

Bonjour

Les lois du transfert de chaleur s'appliquent toujours, par contre ce n'est plus forcément le cas pour les paramètres physiques des matériaux utilisés : Le Cp et la conductivité varient plus ou moins en fonction de la température, et on peut rencontrer des phénomènes de variation d'enthalpie très importants, en particulier avec les polymères (fusion, transition vitreuse...)
Pour une approche plus réaliste il faudrait effectuer une simulation par éléments finis en 3D, et renseigner correctement les lois de variation de température en fonction de l'énergie reçue ; on peut le faire sur Solidworks par exemple.

[Sethy]

Où situer la limite d'une propriété macroscopique comme la température d'un matériaux ?

Evidemment, je parle de la température d'un matériaux considérée habituellement comme une fonction de l'espace et du temps. Fonction "suffisamment" continue pour qu'on puisse à appliquer des opérateurs comme la dérivée, le gradient, etc.

Or, on sait bien qu'au niveau moléculaire ou atomique, une telle fonction n'existe pas. A la place, il y a une distribution de population entre différents niveaux d'énergie de vibration et rotation.

D'où ma question : peut-on encore parler de gradient (ou si oui, quel sens physique lui donner) ?

[RomVi]

On est quand même plusieurs dizaines d'ordres de grandeurs en dessous de la taille d'un transistor... Les mêmes lois continuent à s'appliquer.

[Antoane]

Bonjour et merci pour vos réponses.

Les lois du transfert de chaleur s'appliquent toujours, par contre ce n'est plus forcément le cas pour les paramètres physiques des matériaux utilisés : Le Cp et la conductivité varient plus ou moins en fonction de la température

Pas de problème, je prend ça en compte.

, et on peut rencontrer des phénomènes de variation d'enthalpie très importants, en particulier avec les polymères (fusion, transition vitreuse...)

Dans mon cas c'est surtout du semi-conducteur (Si, SiC ou GaN) et une métallisation aluminium - dont la chaleur latente de fusion est prise en compte.
Vois-tu d'autres paramètres dans le genre ?
Il y a éventuellement l'epoxy du sur-moulage, mais l'hypothèse généralement formulée est que sa conductivité est suffisamment basse pour que la chaleur reste dans la puce.

Pour une approche plus réaliste il faudrait effectuer une simulation par éléments finis en 3D, et renseigner correctement les lois de variation de température en fonction de l'énergie reçue ; on peut le faire sur Solidworks par exemple.

Y a-t-il une raison de faire ça en 3D, mis à part pour les effets de bord ?
Quitte à faire de la 3D, il faudrait réussir à modéliser les cellules, les points chauds et la réparation des courants et potentiels sur la surface de la puce, mais ça représente un vrai travail de modélisation - sans compter les problèmes numériques.
Sinon, on suppose que ça marche bien en 1D, le ratio de la longueur de la puce sur la profondeur de diffusion de la chaleur est de l'ordre de 50

[RomVi]

Avec un rapport pareil la simulation en 1D est réaliste.
Serait il possible d'avoir plus de détails pour que je puisse regarder de mon coté ?

[Sethy]

On est quand même plusieurs dizaines d'ordres de grandeurs en dessous de la taille d'un transistor... Les mêmes lois continuent à s'appliquer.

OK.

Mais quelle est l'épaisseur de la jonction ?

[Antoane]

Bonjour,

Merci pour vos réponses.

> Mais quelle est l'épaisseur de la jonction ?
En l’occurrence, je traite d'un transistor MOSFET, il n'y a donc pas de jonction (1er quadrant). L'épaisseur de la zone active est de l'ordre de plusieurs µm - environ 8 µm dans mon cas, c'est encore 10^4 à 10^5 atomes d'épaisseur. C'est beaucoup plus dans le cas d'un transistor en silicium.

> Serait il possible d'avoir plus de détails pour que je puisse regarder de mon coté ?
Très volontiers, merci. En PJ un exemple de géométrie :

- la puce est modélisée par une métallisation aluminium d'épaisseur e_Al= 4 µm, placée au dessus d'un bloc de Carbure de Silicium (ou de silicium pur), lui-même d'épaisseur : e_SiC = e_Die - e_Al= 176 µm
- pour ce qui est des conditions aux limites : en x=0 (dessus de l'aluminium) : adiabatique ; en x= e_Die : cela importe peu, on fixe en général la température à celle de l'ambiant.
- la source : une source de puissance (e.g. de 40 kW/cm² - désolé pour les unités d'ingénieur, si c'est plus simple, ça correspond à 8.73E5 BTU/h/in² ) homogène entre les abscisses x=x_j = 4.6 µm et x=x_n+x_j = 12.6 µm (i.e. dans la zone active).
Rien de pressant, je ne reprendrai probablement pas sérieusement la question avant deux semaines.

[obi76]

Salut,

en cas de très forts gradients, pour moi ce n'est plus valable. Déjà parce que la conductivité dépend de la température un minimum, ce qui fait intervenir un terme supplémentaire dans l'équation de la chaleur (termed'autant plus grand que le gradient est important...), et ensuite parce que si on est hors équilibre thermodynamique, la température seule n'est pas capable de modéliser correctement l'agitation thermique de ce que l'on regarde.

[Antoane]

Bonjour Obi,

> la conductivité dépend de la température un minimum, ce qui fait intervenir un terme supplémentaire dans l'équation de la chaleur
Ce terme est pris en compte dans l'équation que je donne en #1 en ne sortant pas le lambda de ou est-ce que tu parles d'un autre terme ?

> si on est hors équilibre thermodynamique, la température seule n'est pas capable de modéliser correctement l'agitation thermique de ce que l'on regarde.
Tu aurais une référence sous la main ? je comprend chaque mot mais ensemble, c'est plus dur
Il me semblait que, justement, la température caractérise l'agitation thermique... mais je ne suis pas physicien.

[Sethy]

Salut,

en cas de très forts gradients, pour moi ce n'est plus valable. Déjà parce que la conductivité dépend de la température un minimum, ce qui fait intervenir un terme supplémentaire dans l'équation de la chaleur (termed'autant plus grand que le gradient est important...), et ensuite parce que si on est hors équilibre thermodynamique, la température seule n'est pas capable de modéliser correctement l'agitation thermique de ce que l'on regarde.

Ce sont exactement les réponse aux questions que je posais dans le post #12 : limite du gradient et limite de le "fonction" température d'un matériaux.

[obi76]

Ce terme est pris en compte dans l'équation que je donne en #1 en ne sortant pas le lambda de ou est-ce que tu parles d'un autre terme ?

Non je parlais bien de celui là (souvent le réflexe est d'essayer de résoudre le laplacien...).

Tu aurais une référence sous la main ? je comprend chaque mot mais ensemble, c'est plus dur
Il me semblait que, justement, la température caractérise l'agitation thermique... mais je ne suis pas physicien.

Oui, la température caractérise l'agitation thermique, mais la manière dont est tirée l'équation de la chaleur repose sur une hypothèse qu'il ne faut pas oublier : qu'on est à l'équilibre thermo. En gros, quand tu prends un ensemble de particules, la température c'est le moment d'ordre 2 de la PDF en vitesse de ces particules. A l'équilibre, cette PDF est une Maxwellienne, et la manière dont les particules interagissent entre elle satisfont l'équation de la chaleur. Sauf que... Ben sauf que si c'est pas une Maxwellienne, l'équation de la chaleur est pour moi fausse (ou au mieux, imparfaite).

Ce sont exactement les réponse aux questions que je posais dans le post #12 : limite du gradient et limite de le "fonction" température d'un matériaux.

Ce qui est plutot rassurant

[coussin]

mais la manière dont est tirée l'équation de la chaleur repose sur une hypothèse qu'il ne faut pas oublier : qu'on est à l'équilibre thermo.

Je ne comprends pas cette partie.
L'équation de la chaleur donne le champ de température dans le cas d'une situation de déséquilibre thermique, non ? Pour moi, l'équilibre thermo est atteint à un temps infini, quand le champ de température est devenu constant dans l'espace.
Je ne comprends pas le sens que vous donnez à équilibre thermo.

[obi76]

Je ne comprends pas le sens que vous donnez à équilibre thermo.

Oui effectivement ce n'est pas clair. L'équilibre thermo c'est à partir du moment où les interactions entre particules fait de sorte à ce que leur PDF (en vitesse) est une Maxwellienne. En fait une Maxwellienne c'est la seule distribution en vitesse qui, malgré une agitation et des transferts d'énergie entre particules permanente - est stationnaire.
Si la PDF n'est plus une maxwellienne (transfert très rapide d'énergie, gradient trop fort, ou particules pas assez nombreuses), alors cette équilibre n'est pas atteint et l'hypothèse nécessaire pour passer des équations de Boltzmann à celles de la chaleur, de NS, ou autres, ne sont plus satisfaites.

[coussin]

OK pour ce critère sur la PDF
Est-ce que ma "définition" de l'équilibre thermodynamique, à savoir un champ de température constant dans l'espace (et dans le temps en fait...) est correcte ?

[coussin]

De plus, la PDF Maxwellienne, c'est seulement pour les gaz. L'équation de la chaleur s'applique aux solides (c'est le cas ici)...

[obi76]

De plus, la PDF Maxwellienne, c'est seulement pour les gaz. L'équation de la chaleur s'applique aux solides (c'est le cas ici)...

Tout à fait, et c'est là que je ne sais pas jusqu'où va la validité de ce que je dis... Parce que dans ce cas : comment est définie la température d'un matériau (ou du moins : sur quelles hypothèses se base-t-on pour définir un flux de chaleur dans un solide ?). Dans un gaz, c'est rigoureusement Boltzmann, mais en matériau... aucune idée. L'extrapolation est sans doutes justifiée mais bon, il faudrait creuser dans cette direction).

[obi76]

De plus, la PDF Maxwellienne, c'est seulement pour les gaz. L'équation de la chaleur s'applique aux solides (c'est le cas ici)...

Hmm je parle localement. Si on prend un domaine adiabatique, pour moi l'équilibre c'est lorsque la PDF ne bouge plus.

[coussin]

Tout à fait, et c'est là que je ne sais pas jusqu'où va la validité de ce que je dis... Parce que dans ce cas : comment est définie la température d'un matériau (ou du moins : sur quelles hypothèses se base-t-on pour définir un flux de chaleur dans un solide ?). Dans un gaz, c'est rigoureusement Boltzmann, mais en matériau... aucune idée. L'extrapolation est sans doutes justifiée mais bon, il faudrait creuser dans cette direction).

Dans un solide, la température est définie comme la population des phonons. On a un spectre de phonons, ils sont peuplés via une distribution de Planck.
Si la population de phonons ne suit pas une distribution de Planck, c'est là qu'on peut avoir des trucs bizarres (comme des températures négatives). C'est peut-être alors le critère d'équilibre thermodynamique, je ne sais pas...

Pour les liquides, je ne sais pas non plus...

[Antoane]

Bonjour,

Je ne creuserai pas davantage la question, mais aurai au moins trouvé matière à ajouter un paragraphe dans la section de discussion du compte-rendu

Merci encore pour vos intéressants échanges.