Calculer la vitesse à partir du théorème de l'énergie cinétique et d'une autre manière

[j o]

Bonjour,
J'ai un exercice de mécanique qui présente un skieur qui descend une pente. On connait seulement son poids, la différence d'altitude entre le début et la fin de la pente, la longueur de la pente et la valeur de la force de frottement de la neige sur le skieur.
L'objectif est de calculer, après avoir défini les travaux de chaque forces en jeu (ici le poids, la réaction normale du sol, et les frottement de la neige),la vitesse de deux manières différentes.
La première est envisageable avec le théorème de l'énergie cinétique avec un référentiel terrestre galiléen. Mais je ne trouve pas de deuxième manière.
Le système n'étant pas énergétiquement isolé, on ne peut pas utilisé le principe de conservation de l'énergie. Et si on utilise la relation delta E_m = somme des travaux, c'est impossible car v= sqrt(2(somme(W)-Ep_i)/m) et c'est en fait une racine d'un nombre négatif.
Merci d'avance pour vos réponses .
-----

[Calvert]

Salut,

connaissant toutes les forces agissant sur le skieur, on connaît son accélération. On peut donc utiliser les relations définie en cinématique pour calculer la vitesse du skieur en bas de la pente.

[j o]

Comment peut-on connaitre l'accélération s'il on ne connait pas le temps écoulé pendant le mouvement? On n'a pas de courbe pour le connaitre ni d'autre informations

[Calvert]

Deuxième loi de Newton ?

[A voir en vidéo sur Futura]

[j o]

Il faut utiliser a mais on ne connait pas le temps t... a= dv/dt donc on a trois inconnus (on peut éventuellement trouver a avec les vecteurs mais il faut t

[Calvert]

On connaît , puisqu'on connaît toutes les forces. On connaît aussi la distance parcourue. Comme toutes les forces sont constantes, on sait que l'accélération sera constante aussi. Du coup, il faut chercher du côté du mouvement rectiligne uniformément accéléré (2 relations seront utiles). Deux relations pour deux grandeurs inconnues (le temps et la vitesse finale), ça devrait aller...

[j o]

mais la pente n'est pas une droite elle forme une courbe concave

[Calvert]

Voilà une information qu'il aurait été utile de donner dès le début.

Est-ce que tu pourrais donner l'énoncer exact de l'exercice, et éventuellement le schéma qui va peut-être avec ?

[j o]

On néglige durant l'étude les frottement de l'air. un skieur de 70 kg s'élance à vitesse nulle sur une pente dont l'altitude initiale est de 1500 m et l'altitude finale est de 1400 m. La pente comme décrite sur le schéma est longue de 200 m est se termine par une partie horizontale et les frottements de la neige sur le skis sont équivalents à une force constante de 3.10^2 N. 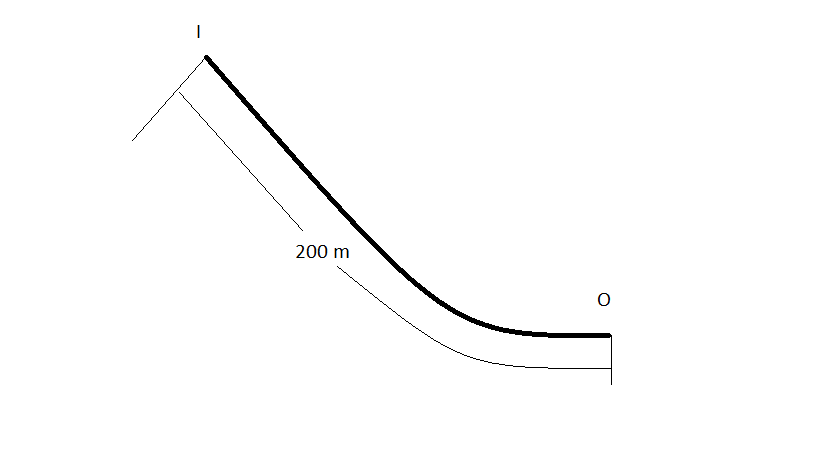Calculer les travaux des forces mises en jeu, et déterminer les caractéristiques du vecteur vitesse avec le théorème de l'énergie cinétique et avec une autre méthode desolé je n'ai pas pensé à le préciser

[j o]

C'est de quel niveau cet exercice?
Je pense qu'il faut utilisé la non-conservation de l'énergie non?

[Dynamix]

Et si on utilise la relation delta E_m = somme des travaux, c'est impossible car v= sqrt(2(somme(W)-Ep_i)/m) et c'est en fait une racine d'un nombre négatif.

Comment tu trouves un nombre négatif ?
Je supposse que tu pars de :
m.g.Δh - F.L = m.v²/2
avec :
m.g.Δh = 70*10*100
F.L = 300*200

Au passage , 300 N de frottement , c' est de la neige d' été ? (verte avec des taches jaunes)

[j o]

oui mais je partais sur le principe que delta_E = somme des travaux de toutes les forces < expression du cours (conservatives et non). là, c'est bon. Merci beaucoup

[j o]

"Au passage , 300 N de frottement , c' est de la neige d' été ? (verte avec des taches jaunes)" c'est beaucoup ou pas. je veux dire la neige a une force plus grande ou plus faible.

[Dynamix]

c'est beaucoup ou pas. je veux dire la neige a une force plus grande ou plus faible.

presque la moitié du poids , c' est beaucoup .