Bonjour, je bloque dans un exercice qui m'a l'air assez simple pourtant. J'ai essayé plusieurs méthodes et à chaque fois j'obtiens une réponse différentes
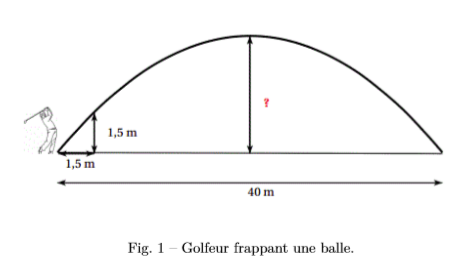
Voici l'enoncé : Un golfeur frappe sa balle avec un angle de 45◦. La trajectoire de la balle est parabolique (on néglige les frottements de l’air). La distance horizontale pacourue par la balle est 40m. Déterminer la hauteur maximale atteinte par la balle.
1ère méthode
Je sais que en x : MRU et en y : MRUA
J'utilise la formule xf = x0 + v0*t avec xf = 40m v0=1,5 m/s
Je trouve t = 26,66 s
La balle effectue la moitié de la trajectoire en la moitié du temps
donc j'utilise la formule y = y0 + v0*t + 1/2 * a*t² avec t = 13,33 s v0=1.5 m/s et a = -9.81 m/s²
J'obtiens y= -847 m (réponse absurde)
2ème méthode
Cette fois je cherche l'équation de la parabole à l'aide des racines et du point p = (1.5 ; 1.5)
Je trouve f(x) = (-2/77)*x² + (80/77)*x
En prenant x = 20 je trouve y = 10,38 m (réponse plus probable)
Et enfin ma 3ème méthode
Il s'agit d'utiliser la formule pour trouver la hauteur h = (v0²*sin²(45°))/2*g
Avec v0 = sqrt (1.5² +1.5²) je trouve h = 0,05m (là encore une réponse bizarre)
Donc voilà, je pense que ma faute vient de la vitesse initiale mais pourtant tout me semble logique.
C'est très frustrant car c'est un exercice assez simple mais je n'arrive pas à trouver la réponse
Je serais reconnaissante si vous m'aidez
Merci
-----