Bonsoir,
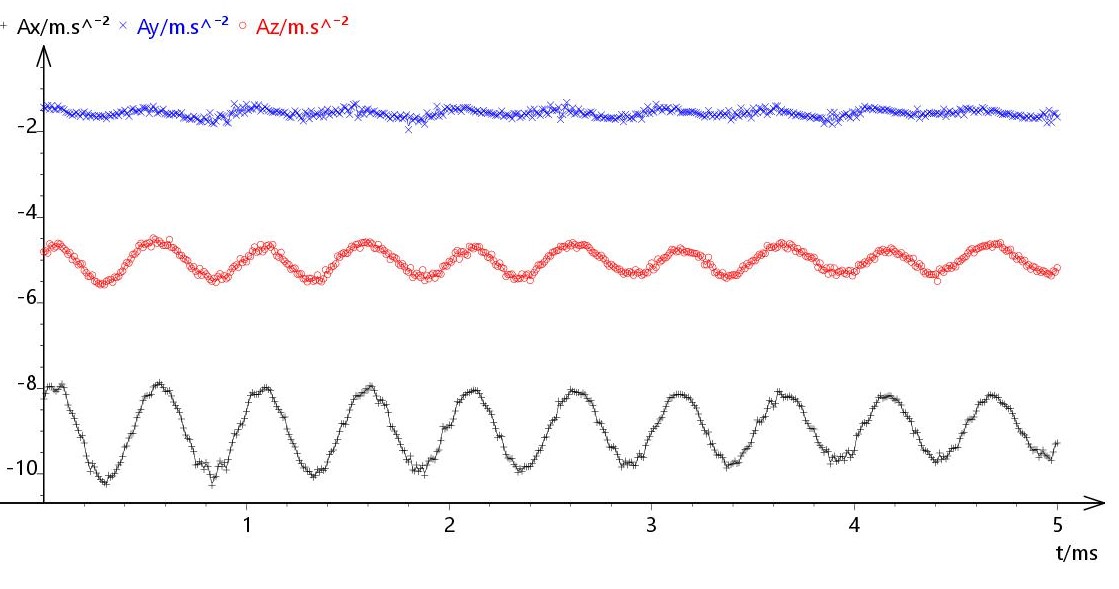
A l'aide d'un accéléromètre, j'ai obtenu les accélérations selon les 3 axes cartésiens (x, y et z) d'une masse au cours d'un mouvement de rotation (pendule simple).
J'aimerais pouvoir remonter à l'accélération angulaire mais je suis bloqué.
Pourriez-vous m'aider ?
Merci
Bonjour,
Considérez un solide en mouvement de rotation autour d'un axe donné (fixe ou mobile selon votre cas), puis déterminez l'accélération d'un point qui sera la point où est placé votre accéléromètre.
Not only is it not right, it's not even wrong!
Remarque : attention à l'accélération de la pesanteur.
Bonjour
Merci, en fait je me suis un peu mal exprimé dans ma demande, désolé : j'aimerais obtenir la solution temporelle d'oscillation du pendule sur les axes x et y.
Je n'ai aucun souci pour déterminer l'accélération dans chacun des 2 systèmes de coordonnées
Pour éviter de traîner la valeur de la tension du fil, je pars du PFD en sphérique en projection surpour arriver à la relation "classique" de l'oscillateur, en considérant l'angle petit on arrive alors à
j'essaye ensuite de basculer en sphérique mais je suis bloqué car en intégrant
Soit vous raisonnez en sphériques et donc vous obtenez
Soit vous raisonnez en cartésiennes et alors
Si vous mélangez les deux, c'est normal que cela soit compliqué.
Je ne comprends pas trop non plus : comment la connaissance de
Dans mon expérience du pendule simple, comme je connais les accélérations selon x et y au cours du temps ; j'aimerais donc connaître les équations du mouvement sur ces axes pour corréler l'expérience à la théorie
Il faudrait préciser votre montage expérimental : je ne vois pas trop comment mesurer avec un accéléromètre les accélérations d'un pendule selon x et y (au sens où vous l'entendez :
Si vous connaissez
J'ai pris un pendule simple auquel j'ai accroché un accéléromètre (LSM9DS1 pour être exact) connecté via Arduino pour la récupération des données.
Les courbes obtenues sont les suivantes :
En fait, ce que je désirai c'était un dessin ou une photo, pas des courbes.
Je m'explique : pour pouvoir mesurer l'accélération selon votre x, il faudrait que la direction Ox reste verticale, ce qui me parait compliqué.
Si vous avez rigidement fixé votre accéléromètre à votre pendule, l'axe des x est en fait l''axe radial et l'axe y l'axe orthoradial.
J'ai fait coincider un des axes avec la verticale du pendule à l'équilibre : il reste donc toujours dans l'axe du fil du pendule.
C'est avec votre réponse que je me dis qu'effectivement, l'accéléromètre étant fixé au pendule, les axes correspondent aux axes radial et orthoradial.
Je dois pouvoir remonter à la valeur de l'angle
OK, c'est bien cela.
Attention à ma remarque du message #3, l'accéléromètre mesure tout l'accélération due au mouvement et l'accélération de la pesanteur (principe d'équivalence oblige).
Sur les courbes obtenues, le décalage d'une valeur d'environ 9 est dû à l'accélération de la pesanteur qui est toujours mesurée sur l'axe vertical ?
C'est bien cela sauf que votre axe x ne reste pas vertical, et la composante de pesanteur va varier (g cos \theta).
D'autre part l'axe y va récupérer aussi une composante de pesanteur (g sin \theta).
Voir le début de : AN3461 (jusqu'à la page 5)
Le LSM9DS1 possède aussi un magnétomètre et un gyroscope, on peut les utiliser simultanément pour s'en sortir : adafruit ... sensor-fusion-algorithms
Ceci étant, sachant que vous avez un pendule avec un mouvement contraint, il doit être possible de récupérer les deux accélérations voulues.
Autre référence claire : https://arxiv.org/pdf/1406.3867.pdf
