expérience EPR simulée en local

[invite0bbfd30c]

Si j'ai bien compris, les équations (18) et (19) dans l'article de Clauser et Horne sont des "fonctions de blocage" analogues à celle d'imul ?

Pas tout à fait, c'est la probabilité totale de détection. Celle d'imul est décomposée en deux parties.
-----

[Pio2001]

Voyons si j'ai compris comment ça marche.

Si on prend l'inégalité CHSH (celle-là je la connais bien) :



Le principe de la fonction de blocage d'imur consisterait à donner des poids différents aux différents termes, en fonction des angles considérés ? C'est ça, le "unfair sampling" ? Rajouter une pondération pour favoriser certains termes par rapport aux autres ?

Mais alors le flux de photons ne serait pas le même selon l'angle du polariseur... sauf si la source pondère le flux de photons en fonction de la variable cachée de sorte que ça compense ?

Et pour que ça marche dans toutes les directions... on construit une fonction de blocage qui fait en sorte que quand on redonne du poids à l'un des termes, cela en enlève automatiquement à un autre ?

[invite955d864a]

J'ai fait le test avec l'inégalité d'Eberhard, mais pas de chance, pas violée...
j'obtiens J/N = 0.039 (il faut une valeur négative, théoriquement -0.207)

Dans leur expérience ils obtiennent -0.00524
Mais elle est plus complexe, et nécessite un intrication faible pour violer l'inégalité. (ce qui me semble pas très logique pour le moment)
Il faudrait que je simule leur expérience pour tout comprendre.
Il ont un taux d'erreur dans les bras de mesure.
Je ne comprend pas pourquoi elle est violée qu'à certains angles.
Pas simple..

[invite955d864a]

Le unfair sampling, c'est quand les photons détectés ne sont pas représentatifs de l'ensemble des photons émis.
C'est ce qui se passe avec ma méthode pour les détections de coïncidences, parce-que ce qui est décorrélé est filtré.
Ça peux se produire aussi si il y a des mauvais réglages dans l'expérience, des dissymétries de détection.

[invite955d864a]

sauf si la source pondère le flux de photons en fonction de la variable cachée

Pas mal cette idée, à garder sous le coude, ça peux servir

[invite955d864a]

J'ai du nouveau intéressant

C'est normal que ma méthode ne viole pas l'inégalité d'Eberhard sinon ça signifierait qu'elle n'est pas locale. (Et un bug dans le programme de test)
J'ai utilisé la forme originale de l'inégalité. (prise en compte de oo, ee, oe, ou, eo, uo)

J'ai étudié l'expérience "Bell violation with entangled photons, free of the fair-sampling assumption". (lien donné par Chip)
Voici leur système



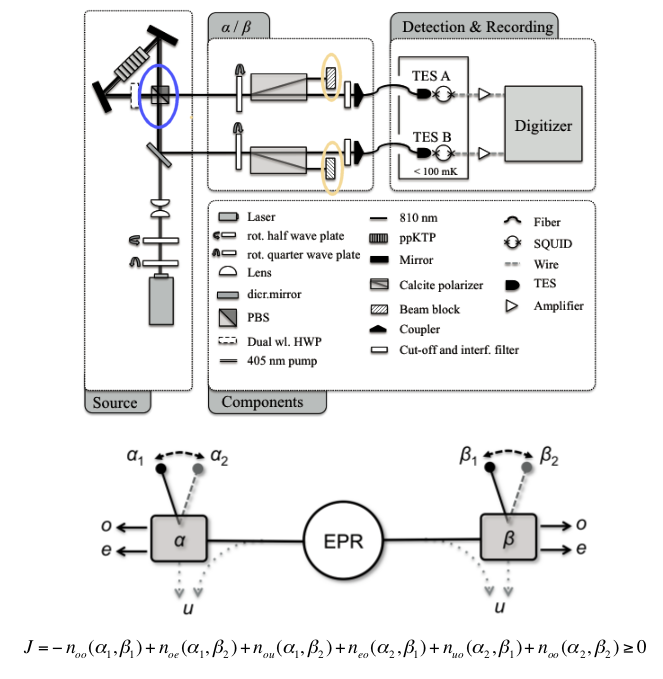
Avec mon interprétation, leur expérience ne fait pas le test correctement.
Si on regarde l'image, les 2 photons intriqués passent dans le PBS (polariseur séparateur) qui est fixe.. (rond bleu)
Les mesures se font ensuite en réglant les "wave plate" sur les photons polarisés.
Les PBS pour les deux photons étants parfaitement alignés (vu que c'est le même), on n'est pas correctement dans les conditions d'Eberhard.
D'abord la corrélation est toujours maximale dans ce cas (diff angle = 0 ou 90), ensuite les angles utilisés pour leur expérience ne s'appliquent pas directement aux photons de la source.

J'ai simulé leur expérience avec mon système local, et je viole bien l'inégalité pour leur combinaisons d'angles, j'obtiens J = -0.167 .
J'ai mis le code ici, si quelqu'un à envi de vérifier ça serait bien, car c'est assez complexe et il y a peut être une erreur.

epr_eber.c

J'ai un doute sur la valeur J/N, je me demande si N = nombre d'échantillons sur les 4 mesures, ou une seule.
Dans leur expérience ils utilisent N pour une mesure alors que les compteurs concernent 4 mesures, je comprend pas trop.
Mais si c'est que ça c'est pas trop grave ça change pas le signe du résultat.
Il y a aussi un miroir sur Bob qui fait tourner sa polarisation de 90° si je me trompe pas.

[invite955d864a]

J'espère ne pas faire de "flood",
J'ai fait une dernière page web pour finir ce projet sur lequel j'ai passé déjà beaucoup de temps.

Epr_local.htm

[Deedee81]

Salut,

J'espère ne pas faire de "flood",

Un peu

Mais la difficulté va surtout être d'avoir quelqu'un ici qui a le temps de regarder tout ça (y a du volume). En tout cas étant au boulot.... j'ai pas trop le temps, et c'est dommage car c'est un sujet que j'aime bien.

[Kiraxel]

beaucoup doivent trouver ça intéressant et il doit y avoir aussi suffisamment de participants compétents sur ce sujet

Je confirme je trouve cela intéressant. Tout ce qui concerne le paradoxe EPR et les inégalités de Bell sont intéressantes.
Mais je ne suis pas assez fort en programmation et en physique pour y participer.

En tout cas c'est un plaisir de vous lire.

[invite955d864a]

Bonjour,

J'ai trouvé une simu EPR sur github ici https://github.com/michel4j/epr-clocked

C'est écrit en python.
Il simule la source, les détecteurs, et l'acquisition.

La corrélation QM résulte de délais de transmission variables des photons au niveau des polariseurs.
Ce délai dépend de l'angle de polarisation du photon par rapport au polariseur, et donc du temps nécessaire pour 'repolariser'.
Il dépend aussi dans cette simu d'une variable cachée aléatoire ayant une distribution spéciale.

Ces délais variables génèrent des difficultés pour identifier les paires de photons intriqués et rend les mesures de corrélation difficiles.
On peux par exemple dans certains cas détecter des photons dans le mauvais ordre d'émission.
Cela semble être la principale piste étudiée actuellement pour obtenir une explication réaliste.
La simulation sur github reproduit bien les corrélations QM mais nécessite une fenêtre d'analyse très petite (inférieure à 1nS, ce qui ne semble pas réaliste).

J'ai fait un portage du code python en C et modifié la méthode, ça permet d'agrandir la fenêtre d'analyse jusqu'à 5nS et d'augmenter le nombre de paires détectées.
Je n'utilise plus qu'une seule variable cachée qui est la polarisation du photon.
L'idée est la même que dans mon précédent programme et je suppose que le temps de transmission augmente (non linéairement) lorsque la différence d'angle se rapproche de PI/4 (éguillage).

J'ai mis le code ici

[invite955d864a]

Bonjour,

Pour ceux qui s'intéressent toujours à ce sujet, j'ai abandonné la méthode décrite jusqu'à maintenant basée sur un filtrage.
Elle a l'inconvénient d'utiliser un comportement dépendant du type de photon (intriqué ou non, donc nécessitant une information locale permettant de définir le comportement du polariseur).

J'ai fait une une nouvelle méthode qui est identique quelque soit le type de photon.
Les corrélations sont alors la conséquences de la distribution des valeurs d'une variable cachée qui est commune aux deux photons, et d'un algorithme qui sélectionne la sortie du polariseur en utilisant le principe de moindre action.

J'ai mis le projet sur github ici: (et une version en Français ici)

[Pio2001]

Bonjour Imul,
Je ne suis pas arrivé à suivre le détail des tes derniers développements.

Ce serait intéressant d'avoir un résumé des résultats obtenus. On a vu plus haut avec Chip que ta première simulation parvient à violer l'inégalité de Bell sans faire appel à des variables cachées non locales, en introduisant des non-détections, ce qui correspond à la faille (loophole, en anglais) du "fair sampling" (échantillon représentatif).

Chip a ensuite donné un lien vers l'inégalité d'Eberhard, qui est une inégalité de Bell qui prend en compte la faille du fair sampling (*).
Et on a vu que ta simulation, qui est à variables cachées locales, ne viole pas cette ingégalité. Donc tout va bien.

Ensuite, quel est le résultat obtenu dans ton message 66 ? Tu dis que tu violes une inégalité d'Eberhard en simulant leur expérience, mais comment ça se fait ? Tu peux violer cette inégalité avec une simulation à variables cachées locales ? Ou c'est autre chose qui cloche ?

Ensuite dans ton message 70, tu parles de la fenêtre d'analyse. En quoi ça consiste ? C'est la fenêtre de temps dans laquelle on considère que deux photons appartiennent à une même paire ? Est-ce que ce paramètre est pris en compte dans l'inégalité d'Eberhard ? Se tromper dans l'identificatuion d'une paire ne revient-il pas à introduire un peu de unfair sampling ?

Enfin, quel est l'avantage de ta dernière méthode ? Est-ce qu'elle viole toujours l'inégalité de Bell sans violer celle d'Eberhard ?

(*)Article de 2013 du groupe Zeilinger "Bell violation using entangled photons without the fair sampling assumption", M. Giustina et al., Nature 497, 227 (2013) :
https://www.nature.com/articles/nature12012
https://arxiv.org/abs/1212.0533
https://arxiv.org/pdf/1212.0533

[invite955d864a]

Bonjour Pio2001,

Ça fait beaucoup de questions d'un coup

Ce serait intéressant d'avoir un résumé des résultats obtenus.

Tu peux voir les résultats de la dernière méthode en suivant le lien en bas de mon précédent message (71).
En fin de première page il y a un lien sur les graphiques, et à la fin des graphiques un lien expliquant le fonctionnement.

Ensuite, quel est le résultat obtenu dans ton message 66 ? Tu dis que tu violes une inégalité d'Eberhard en simulant leur expérience, mais comment ça se fait ?

Cela est du au fait que la méthode produit des double blocages ne générant aucune mesure, et cela dans les situations où les corrélations sont minimales. (aux différences d'angles proche de n*45°)
Les cas restants, générant au moins une mesure simple, représentent alors un sous ensemble qui est globalement plus corrélé que l'ensemble émis.

Cela permet de violer l'inégalité, mais légèrement car les doubles blocages représentent une faible proportion des paires émises.

Je suppose, mais c'est un point théorique dont je ne suis pas sur, que l'inégalité d'Eberhard est applicable seulement si on considère les mesures simples comme uniformément réparties sur l'ensemble des échantillons, et correspondant à des erreurs de détection.

Si elles sont la conséquences d'un blocage sélectif, l'inégalité peut être violée en restant réaliste.
Je n'ai aucune idée comment démontrer ça mathématiquement, mais c'est ce que j'ai observé en simulation.

Dans dans mon dernier code (test_eber.c), j'utilise ce fait en générant des mesures simples uniquement sur les paires ne générant pas de corrélation (qui peuvent être prédites localement en temps réel), ce qui permet d'obtenir un J/N pouvant atteindre -0.085. C'est une valeur éloignée du maximum théorique (-0.207), mais beaucoup plus élevé en valeur absolue que -0.00524, qui est la valeur obtenue par l'expérience de référence sur le fair sampling de 2013 de M.Giustina

Mais de toutes façon j'ai abandonné cette méthode car elle présente l'inconvénient de générer une loi de Malus non standard, et il est difficile d'expliquer pourquoi un photon intriqué aurait plus tendance à être bloqué qu'un photon "normal". (qui lui ne l'est pratiquement pas)

C'est ce que m'a dit un physicien qui fait de la recherche et qui m'a incité à chercher une autre explication.

Ensuite dans ton message 70, tu parles de la fenêtre d'analyse. En quoi ça consiste ? C'est la fenêtre de temps dans laquelle on considère que deux photons appartiennent à une même paire ? Est-ce que ce paramètre est pris en compte dans l'inégalité d'Eberhard ? Se tromper dans l'identificatuion d'une paire ne revient-il pas à introduire un peu de unfair sampling ?

Les sources de photons intriqués qui utilisent un laser dit 'pumped' peuvent envoyer des paires à des intervalle de temps très proches, et le délai entre deux envois est variable, avec une distribution temporelle spécifique (type beta pour celles que j'ai pu trouver).

Il faut alors ajouter aussi le délai lorsque le photon traverse le polariseur qui est variable.
Si on accepte une vue en mode réaliste avec existence initiale de la polarisation du photon, cela dépend de l'angle relatif avec le polariseur, de la longueur d'onde du photon et des caractéristiques du polariseur.

Donc au final il y a plein de détections rapprochés dans le temps, et il faut pouvoir identifier lesquelles appartiennent à la même paire émise.
On peux avoir un délai entre le photon le plus retardé de la paire n et celui le moins retardé de la paire n+1 qui est inférieur au délai de détection entre les deux photons des paires n ou n+1.
Et dans le lot peuvent se glisser aussi des détections de photons simples, ou des paires de photons simples non intriquées.

Donc en pratique, faire les association de manière fiable n'est pas facile et il faut bien calculer la largeur de la fenêtre. Si elle est trop petite, on obtient une bonne fiabilité dans l'association des paires, mais beaucoup de mesures simples, et si trop large on augmente les erreurs d'appairage.

Ce paramètre n'est pas pris en compte dans l'inégalité d'Eberhard qui suppose des mesures fiables.
Si on se trompe dans l'appairage ça fausse les résultats. (Il faut estimer l'erreur min/max)

Enfin, quel est l'avantage de ta dernière méthode ? Est-ce qu'elle viole toujours l'inégalité de Bell sans violer celle d'Eberhard ?

La nouvelle méthode ne fait pas de blocage et est surtout identique quelque soit le type de photon.
Elle permet aussi de générer la loi de Malus précisément.
Elle n'utilise basiquement que des opérations simples, soit additions/soustractions qui peuvent représenter des interactions physiques élémentaires (pas de fonctions trigo ou autre)

Si on considère une expérience idéale avec une source parfaite et des détecteurs parfaits, elle ne viole aucune inégalité.

Cependant elle montre qu'en utilisant un algorithme basé sur le principe de moindre action pour déterminer la sortie du polariseur, il se produit mathématiquement 3 types de corrélations bien distinctes.

Une corrélation de type cos² (dépend de la distribution de la variable cachée)
Une corrélation rectangulaire. (corrélation maximale)
Un bruit uniforme (aucune corrélation).

Les ratios dépendent de la distribution d'une variable cachée commune aux deux photon.

La partie intéressante est que le type de corrélation peux être prédit localement photon par photon en générant une information (bit d'état) qui identifie les photons qui on subit une repolarisation supérieure à PI/4 en passant dans le polariseur.

Alors les photons qui ont une identification différente ne génèrent aucune corrélation. (bruit uniforme)
Cela est mathématique, et peux s'appliquer à n'importe quel objets utilisant le même algorithme de sélection de chemin.

On peux alors ensuite montrer que pour une expérience non parfaite générant des mesures simples, dès qu'il existe une dissymétrie dans la probabilité de détection des deux états, alors l'expérience apparait naturellement comme non locale, car les mesures simples se produisent principalement sur les paires ne générant pas de corrélations.

Cela se produit très rapidement, et avec seulement 1% de mesures simple, l'inégalité d'Eberhard est alors violée avec J/N = -0.0085
Il se produit la même chose pour les autres inégalités.

Actuellement aucune expérience n'est capable de générer moins de 1% de mesures simples, et cette explication me semble la plus simple pour expliquer les expériences EPR

[Pio2001]

Merci pour les explications ! Je vais digérer tout ça.