Equation différentielle de ce circuit

[111fox]

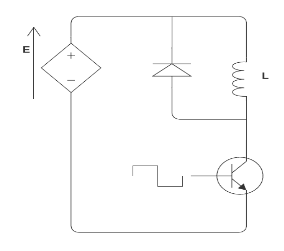
Bonjour les amis, je vous demande s'il vous plait de m'aider à trouver l'équation différentielle relative à ce circuit :



Pour appliquer le champ magnétique B, on utilise un commutateur de tension, c’est un circuit avec un générateur de tension E, un bobinage et un transistor électronique en commutateur, soit ouvert soit fermé. Le bobinage est mis en circuit de diode à roue libre, permettant à l'inductance de se décharger, car même en ouvrant l’interrupteur, la bobine ne peut pas se décharger et donc crée des surtensions dangereuses. Or, là, la diode va venir court-circuiter les surtensions; la diode en régime normal est à l'envers, elle est donc neutre et ne joue aucun rôle, la bobine se charge. Par contre, quand l'interrupteur s’ouvre, la bobine se décharge sur elle-même par l'intermédiaire de la diode de Roue libre.Il faut tenir compte du temps de réponse de la bobine qui vaut L/R, donc de la vitesse limite de modulation.



Je vous remercie pour votre contribution et votre aide, j'ai vraiment besoin de cet équation différentielle

Cordialement,
111fox
-----

[gts2]

Bonjour,

Il n'y pas de résistance ?

[stefjm]

Si, certainement intégrée à la bobine R-L, sinon, ça finirait mal pour le transistor...

[Black Jack 2]

Bonjour,

Il faut plus de précisions sur ce qui est attendu.

Par exemple, si on suppose R la résistance série du bobinage d'inductance L et la diode parfaite (chute nulle en direct (ou d'effet négligeable))

Soit T1 la durée d'un cycle où le transistor est ON et T2 la durée d'un cycle où le transistor est OFF

Soit i le courant dans le bobinage.

En prenant l'origine d'horloge (t=0) au début de la conduction du transistor, lorsque le cycle devient répétitif, on arrive à :

i(t) = E/R + (Io - E/R).e^(-R/L .t) pour t compris dans [0 ; T1]
i(t) = [E/R + (Io - E/R).e^(-R/L .T1)] * e^(-R/L .(t-T1)) pour t compris dans [T1 ; T1+T2]

Avec Io = E/R (1 - e^(-R/L .T1))/(e^(R/L T2) - e^(-R/L .T1))

Un exemple numérique :
E = 10V et R = 1 ohm L = 0,01 H et T1 = T2 = 1 ms

i(t) = 10 - 5,25*e^(-100*t) (pour t dans [0 ; 10^-3] s)
i(t) = 5,25.e^(-100*(t - 0,001)) pour t dans [10^-3 ; 2.10^-3] s)

Le courant dans la bobine oscille donc entre 4,75 A et 5,25 A (fréquence = 1/(2.10^-3) = 500 Hz

Calculs non vérifiés.

*****

Mais si on suppose R quasi nul ou la tension de chute directe dans la diode d'effet non négligeable ... il faut tout refaire.

Pareil si on veut déterminer le "démarrage" à partir d'un courant nul par exemple, donc trouver le régime transitoire jusqu'à ce que le cycle se stabilise (se répète à l'identique).

[A voir en vidéo sur Futura]