Fibre optique & polarisation - Incertitudes mesures

[invite0e793e59]

Bonjour,

Dans le cadre d'une mesure de dégradation du taux d'extinction de la polarisation (PER) d'une soudure entre deux fibres optiques, je dois réaliser un banc de mesure du PER et je souhaiterais en évaluer l'incertitude de mesure.

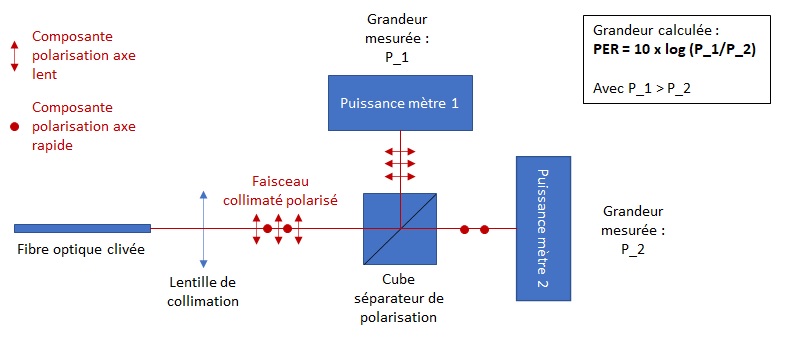
Le banc est représenté dans l'image jointe :


Le signal dans la fibre est polarisé, majoritairement selon un des deux axes de polarisation (cas de l'image : majoritairement selon l'axe lent).
Le PER correspond au log10 du rapport Puissance axe de polar majoritaire (en W) / Puissance axe de polarisation minoritaire (en W), le tout multiplié par 10.

Pour quantifier la dégradation du PER d'une soudure, je déroule la méthode suivante :
- Mesure PER fibre clivée A
- Soudage des fibres A et B
- Mesure du PER fibre clivée B
- Calcul dégradation du PER : d_PER = PER_B - PER_A

L'incertitude de mesure sur chaque puissance-mètre est considéré de +/- 3 % (donnée fabricant).

Mon but est de remonter à la précision de la valeur d_PER.

Pourriez-vous me dire si mes suppositions ci-dessous vous paraissent bonnes ?
- L'incertitude de d_PER (I_d_PER) est égale à la somme des incertitudes de PER_A et PER_B (I_PER_A ou I_PER_B).
- L'incertitude de chaque mesure de PER (_A ou _B) peut être calculée de la manière suivante :
I_PER = PER_max - PER_min
--> PER_max = 10*log(P_1_max/P_2_min)
avec P_1_max = P_1*(1+0.03) et P_2_min = P_2*(1-0.03)
--> PER_min = 10*log(P_1_min/P_2_max)
avec P_1_min = P_1*(1-0.03) et P_2_min = P_2*(1+0.03)

Qu'en pensez-vous ?

Enfin, la signal laser injecté dans les fibres optiques provient d'une source avec une précision sur son PER de +/- y %.
Comment cette incertitude peut-elle être intégrée dans le calcul d'incertitude de d_PER ?

Cordialement,
MacChoff
-----

[invite0bbfd30c]

- Mesure PER fibre clivée A

Avant tout, pourrais-tu décrire ta procédure pour mesurer le PER plus en détail? As-tu des éléments te permettant d'ajuster la polarisation (polariseur, lame quart d'onde, lame demi-onde ...) en entrée et/ou en sortie de la fibre, et/ou l'angle de la fibre en entrée et/ou en sortie?

Petite remarque annexe : sur ton schéma la séparation de polarisation par ton cube n'est pas correcte, la polarisation p est transmise, pas réfléchie. Ce n'est pas important ici, mais autant le savoir

[invite0e793e59]

Bonjour Chip,

A l'heure actuelle, je pensais partir sur un support rotatoire de la fibre clivée afin d'ajuster l'alignement des axes de polarisation de la fibre avec le cube et ainsi de maximiser la valeur de PER.
La fibre est clivée droite --> angle de clive < 1° (vérification à la soudeuse)

Ensuite, via le logiciel de lecture des puissance-mètres, je calcule le PER à partir des deux valeurs de puissance mesurées.

Et merci pour ta remarque : je suis allé un peu vite en faisant le schéma.