Problème archimédien

[soliris]

Bonjour,

Afin de résoudre un problème d'installation d'un jeu de pression, voici comment ça se présente.



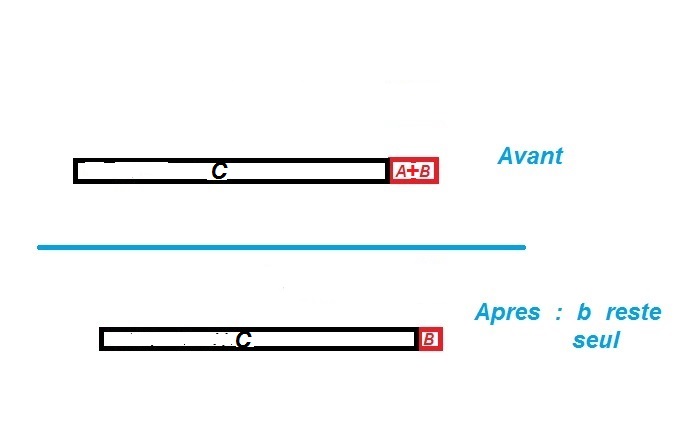
Deux sas sont remplis de chaque côté d'un certain volume de gaz, tous les deux à une pression identique, et sont séparés par une paroi mobile (je précise, sensible à la moindre variation de pression). Le sas noir (C) présente un volume de n fois celui du sas rouge (A + B).

D'un seul coup, le sas rouge perd la moitié de la masse de son gaz (il perd "A") . Quel sera le volume de ce même sas rouge, à ce moment-là, sachant que le sas noir, en C, est resté avec la même quantité de gaz ?
-----

[obi76]

BOnjour,

si tout reste à la même température, on a Vc' (après) = (Va+Vb+Vc)/(1+Vb/Vc) .
Du coup Vb' = Vc+Va+Vb - Vc'.

[soliris]

Merci obi76.

J'essaie de comprendre le cheminement.
L'astuce c'était évidemment de tenir compte de Vc'.

[obi76]

Vous posez les gaz parfaits, sachant que Pa=Pb=Pc et Pb'=Pc', et que Va+Vb+Vc=Vc'+Vb'.

[A voir en vidéo sur Futura]

[soliris]

Vous posez les gaz parfaits, sachant que Pa=Pb=Pc et Pb'=Pc', et que Va+Vb+Vc=Vc'+Vb'.

Oh, d'accord.. Dans ce cas mon dessin est quelque peu erronné; il semble suggérer une perte de volume, alors que dans l'énoncé il ne s'agit que d'une perte de masse (ou de quantité de matière). Remarquable.

[obi76]

Si vous vous amusez à faire varier le volume total, alors il faudrait peut-être le spécifier (et du coup : de quelle manière)...