Problème de trigo dans l'espace

[Cap2Nor]

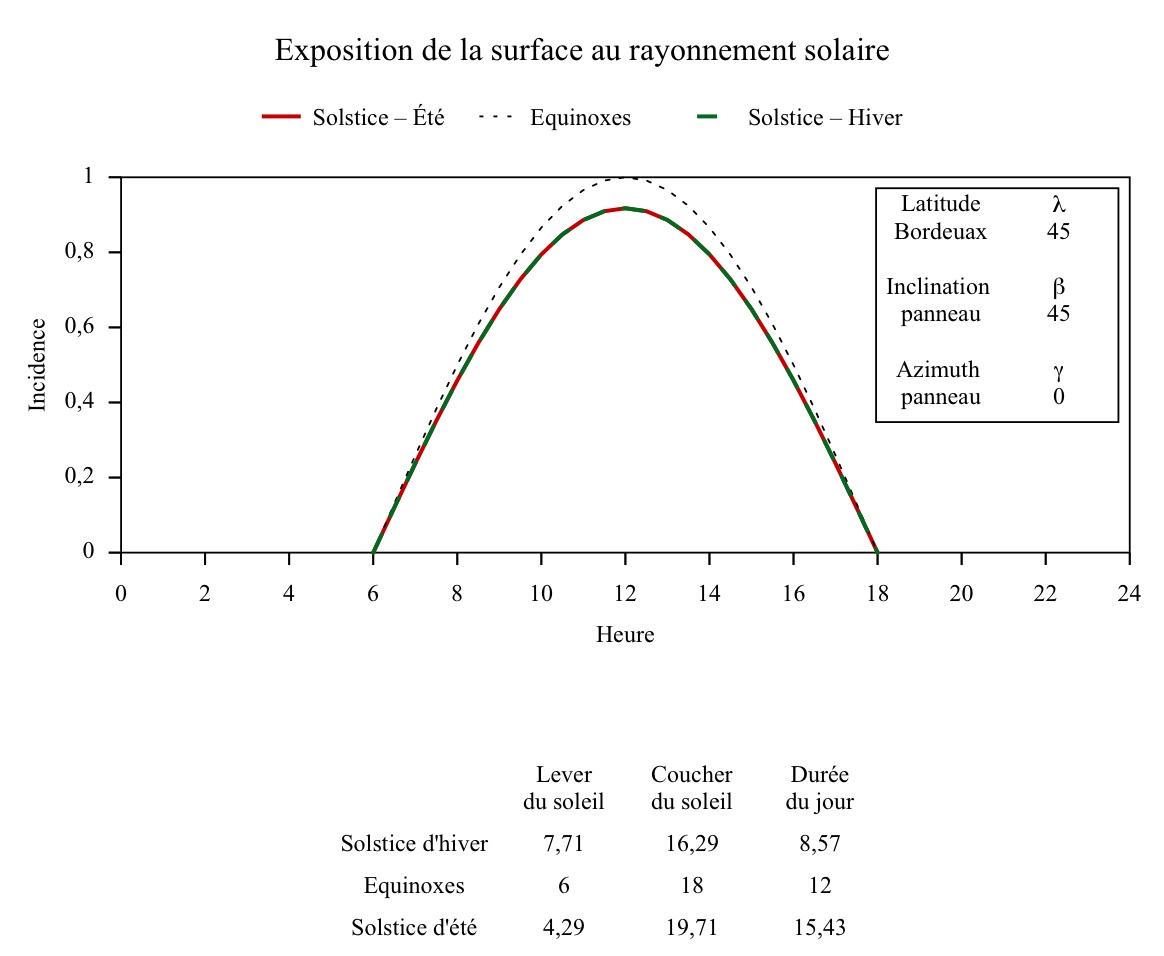
Bonjour à tous,

On me pose un problème auquel je pensais pouvoir répondre rapidement, mais ce que j'obtiens ne satisfait pas mon intuition

Voici la question :
On a un panneau solaire orienté vers le sud avec un inclinaison donnée (paramètre variable). Quel sera le flux solaire reçu au long de la journée ?

Pour résoudre ce problème, j'ai considéré que, vu du Soleil, la base et le sommet du panneau dessinaient deux ellipses (projection de deux cercles inclinés sur le plan écliptique).
La largeur efficace du panneau variera suivant le sinus de l'angle de rotation de la Terre sur son axe, tandis que la hauteur efficace du parallélogramme sera déterminée par l'intersection des deux ellipses.

Cette hauteur est la différence entre les ordonnées des projections des trajectoires de la base et du sommet du panneau, soit :
en prenant r+dr, le rayon du cercle parcouru par le sommet du panneau
et dL la latitude de celui-ci
avec dr/dl = tg Bêta (inclinaison du panneau)
Thêta : l'angle de rotation autour de l'axe de la Terre
Delta: l'angle d'inclinaison de la Terre vis-à-vis du Soleil

h = (r+dr) cos Thêta cos Delta + dL cos Delta - r cos Thêta cos Delta = (dr cos Thêta + dL ) cos Delta

Pour le point remarquable h=0, cette condition ne dépend pas de l'inclinaison apparente de la Terre…

Où est l'erreur ?
-----

[phys4]

Bonjour,
Vous avez choisi une approche compliquée et peu usuelle.
Pourquoi ne pas calculer seulement l'angle du soleil avec la normale au panneau ?
Vos conditions sont peu claires, comment est posé le panneau ?

[Cap2Nor]

Bonjour phys4,

On suppose le panneau orienté plein sud et on cherche à connaître l'influence de l'angle par rapport à l'horizontale sur l'éclairement du panneau. Intuitivement, plus cet angle est important et moins il sera efficace par soleil rasant…

J'ai calculé l'angle du soleil par rapport au sol, mais je m'embrouille lorsque le panneau fait un angle avec l'horizontale…
Quelle est la surface efficace (flux solaire reçu) ?
Cela fait plus de quarante ans que je n'ai pas fait de trigo dans l'espace et les neurones consacrés à cette tâche sont grippés.

En écrivant ce post, je me suis rendu compte qu'il fallait suivre les coordonnées des quatre coins du panneau pour être cohérent avec ma démarche.
L'ombre projetée du panneau (sur un plan perpendiculaire au rayonnement solaire) n'est rectangulaire qu'à midi au soleil. Le reste de la journée, elle prend la forme d'un parallélogramme que je décrivais mal. Je vais sans doute finir de m'en sortir avec un tableur, mais ça manque d'élégance…

[phys4]

Bonjo
En écrivant ce post, je me suis rendu compte qu'il fallait suivre les coordonnées des quatre coins du panneau pour être cohérent avec ma démarche.

C'est trop compliqué : pour n'importe quelle forme de panneau plan, l'éclairage reçu est proportionnel à la surface du panneau et au cosinus de l'angle formé par la direction du soleil et la perpendiculaire au panneau.
Il suffit donc de calculer un seul angle.
Le calcul devient très simple si en plus vous inclinez le panneau pour qu'il soit parallèle à l'axe de la terre, vous avez l'oscillation saisonnière de plus ou moins 23° et la rotation de la terre en 24 H. Après tout dépend de la précision recherchée, faut-il prendre en compte l'équation du temps ?

[A voir en vidéo sur Futura]

[Cap2Nor]

Non. Pas besoin d'introduire l'équation du temps. Je cherche une position optimisée, mais sans pilotage.
On cherche à caractériser la courbe d'éclairement du panneau au cours de la journée, aux différentes saisons, en fonction de l'angle d'orientation du panneau choisi…
L'optimum n'est pas forcément le maximum, mais peut être le plus régulier, sur 24h ou sur l'année…
Je suis à peu près à l'aise dans le plan, mais pas du tout en 3D…

[Cap2Nor]

Il suffit donc de calculer un seul angle.

J'ai besoin de me rafraîchir la mémoire, mais je n'arrive pas à trouver de sites qui traite du calcul de l'angle résultant d'angles non coplanaires…

[Sethy]

Dans la mesure où on peut considérer les rayons solaires comme parallèle entre eux, est-ce vraiment un problème ?

Il suffit de faire une translation et de prendre "au choix" celui qui passe par la base de la normale au panneau.

[Cap2Nor]

Il suffit de faire une translation et de prendre "au choix" celui qui passe par la base de la normale au panneau.

Bien sûr… Toutefois, quand je tape "orientation du soleil" dans un moteur de recherche, je n'ai que des présentations lorsque le soleil est au zénith. Je n'ai rien trouvé indiquant comment calculer sa position à une heure quelconque de la journée. Ou, alors, j'ai des formulaires tout fait qui donnent le résultat. C'est bien pour vérifier mes calculs, mais ça ne m'aide pas vraiment à construire mon repère.
Je vais y arriver. Vous m'avez convaincu de changer d'approche. Il "suffit" quand on manie cela régulièrement. Pour moi, c'est il "faut" et c'est un peu galère à force de tourner le problème dans tous les sens…

[ansset]

Bien sûr… Toutefois, quand je tape "orientation du soleil" dans un moteur de recherche, je n'ai que des présentations lorsque le soleil est au zénith.

c'est normal, et c'est le plus utile pour les panneaux solaires.
https://news.dualsun.com/installatio...nneau-solaire/

Je n'ai rien trouvé indiquant comment calculer sa position à une heure quelconque de la journée. Ou, alors, j'ai des formulaires tout fait qui donnent le résultat. C'est bien pour vérifier mes calculs, mais ça ne m'aide pas vraiment à construire mon repère.

je n'ai pas compris si tu voulais optimiser ton systeme avec une orientation variable.
il existe des installations avec moteur intégré qui suivent le parcours du soleil.
https://www.lumioo.com/?campaignid=3...78269859&adid=
mais j'imagine que ça ne marche pas pour les toitures et j'ignore si le gain éventuel est rentalibisé par l'investissement supplémentaire.

[Cap2Nor]

Il s'agit d'installations fixes, pour lesquelles on veut connaître le flux solaire capté tout au long de la journée (pas seulement à midi) aux différentes saisons…
L'angle du panneau avec l'horizontale est une valeur paramétrique et non une variable ajustable.

[ansset]

s'il s'agit d'installations fixes , alors la meilleure orientation ( préconisée ) est bien vers le sud géographique.
ou bien je n'ai pas compris ce que tu voulais optimiser de plus.
( l'angle est lui , donné dans le premier lien )
ps: pour connaitre le flux ( théorique ) , il est peut être possible de se renseigner auprès des installateurs ou sur le net.

[gavroch]

Bonsoir, je donne des représentations de schémas de votre problème.photo3.png4

[gts2]

Tout est fait dans le lien que vous donnez, il faut simplement aller à la pèche :
p 441 la première formule donne l'angle d'incidence , comme ce qu'il faut est le cosinus il faut prendre le zzz qui dépend de et
p 440 (4) donne en fonction de
p 440 (2) donne
...

Plus simple master/Calculs_astronomiques_simples donne directement ce que vous cherchez en bas de la page 5/10.

[Cap2Nor]

Merci à vous.

J'étais perdu dans la recherche du bon référentiel. Je suis rassuré par la complexité des équations. Le problème n'est pas si trivial que ça.
Pas évident de trouver la bonne information sur le net si on n'a pas une idée précise où chercher. Je vais pouvoir me mettre au boulot.

[Cap2Nor]

Plus simple master/Calculs_astronomiques_simples donne directement ce que vous cherchez en bas de la page 5/10.

J'ai intégré la formule dans mon tableur et j'ai pu faire quelques simulations. Or, quand j'incline le panneau (s > 0), j'obtiens de curieux résultats avec des cos(θ) < -1 !
Cela ne concerne que les valeurs autour de minuit, donc hors du cadre utile, mais cela pose la question du domaine de validation de cette formule "simplifiée", qui n'est pas précisé dans le texte.

En outre, la formule apparaît comme une somme de 5 produits. cos(θ) = A+B+C++D+E… Il y a la succession de deux signes +, qui peut laisser penser qu'il y a peut-être un sixième terme…

[gts2]

Je viens de tester sans problème, que prenez comme latitude et inclinaison ?

[Cap2Nor]

Latitude 43,46° – Inclinaisons de 0 et 17°
Premier cas : OK. Pour le second (inclinaison de 17°), j'obtiens : cos(θ) = -1,278 (à minuit)
Inclinaison nulle.jpegInclinaison de 17°.jpeg

[gts2]

Je n'ai pas la même chose pour le B , je trouve 0,085 (0.398*0.726*0.292) au lieu de 0,195

(aux erreurs de calcul près ....)

[Cap2Nor]

Vous avez raison. Mes excuses. C'est un bête problème de référence dans mon tableur, malgré plusieurs vérifications…
Merci encore une fois de votre aide.

[Cap2Nor]

J'ai corrigé et je n'ai plus d'aberration de calculs…
Mais, quelque chose me chagrine.
Plus l'inclinaison du panneau est forte et plus longue est son exposition au rayonnement solaire… Intuitivement, je m'attends à une meilleure exposition à midi, mais une moins bonne au lever et au coucher du jour. Le sommet du panneau devrait faire le l'ombre à sa base… Or, avec un panneau incliné, je suis surpris d'avoir un cos(θ) positif avant le lever du jour…
Hiver–0°.jpeg
Hiver–17°.jpeg

[gts2]

Au coucher ou au lever, il ne faut pas oublier que le soleil est à l'est ou à l'ouest.

En hiver, il ne va pas tout à fait jusqu'à l'est, donc le panneau parallèle à l'axe est-ouest est bien éclairé.
En été, c'est l'inverse, et le soir le soleil arrive sur l'arrière du panneau, le panneau n'est plus éclairé avant que le soleil ne soit couché.
Aux équinoxes, c'est pile-poil et l'heure de coucher coïncide avec l'heure d'arrêt d'éclairage.

La courbe bleu représente l'éclairement du panneau, la courbe rouge est positive quand le soleil est présent.

été : ete.png
hiver : hiver.png
équinoxes : equi.png

[Cap2Nor]

Je suis d'accord.
Je suis allé au Cap Nord, voir le Soleil de minuit. Bien que le Soleil soit visible toute la journée, un panneau optimisé pour capter ses rayons à midi, là où il est le plus haut, lui tourne le dos à minuit. Fort de cette expérience, la logique voudrait qu'un panneau incliné par rapport à l'horizontale soit éclairé moins longtemps, qu'un panneau au sol, après le lever du soleil et avant son coucher. Or, j'obtiens l'inverse…

Qu'est-ce qui ne va pas, mon calcul ou mon intuition ?

[gts2]

Votre raisonnement est correct, mais il fonctionne l'été ; l'hiver c'est l'inverse.
En se fiant uniquement au cos \theta la durée est plus longue pour le panneau incliné, mais bien sûr une fois le soleil couché, l'"ombre de la terre" joue et donc les durées d'éclairement sont égales.

[Cap2Nor]

Pour un panneau orienté sud, l'expression se simplifie avec sin(γ) = 0 et cos(γ) = 1 ; on a alors :
cos(θ) = sin(δ)⋅[sin(λ)⋅cos(s) − cos(λ)⋅sin(s)] + cos(δ)⋅[cos(λ)⋅cos(s) + sin(λ)⋅sin(s)]⋅cos(ω)

Pour la latitude λ = 45° (≈ Bordeaux), l’expression devient :
cos(θ) = 0,707⋅sin(δ)⋅[cos(s) − sin(s)] + 0,707⋅cos(δ)⋅[cos(s) + sin(s)] ⋅cos(ω)

Si on prend s = 45°, l’expression se simplifie encore et on a :
cos(θ) = cos(δ)⋅cos(ω)

La limite de réception du flux solaire est (normalement) donnée par cos(θ) = 0 , ce qui donne :
cos(δ)⋅cos(ω) = 0
Soit
cos(ω) = 0 ; quel que soit δ…

En hiver, que ce soit une façade, un toit ou une terrasse, ces surface verront le soleil en même temps. Seul le flux variera…

Qu'est-ce qui m'échappe ?

[gts2]

Bonjour,

Pas d'erreur et cela est vrai dès que inclinaison=latitude, ce qui a comme conséquence que le panneau est perpendiculaire à l'équateur ou au plan contenant le parallèle (je ne sais pas si ce plan porte un nom).

A 6h ou 18h, le panneau est vu de face et est parallèle aux rayons solaires.

Le premier dessin (panneausolaire.png) est inexact : celui qui est correct (panneau.png) indique pour l'axe vertical "plan lever-coucher"

[Cap2Nor]

Bonjour,

Si le panneau est parallèle aux rayons solaires à 6h et 18h (cos(θ) =0), c'est le dos du panneau qui sera éclairé avant 6h et après 18 h… C'est le cas de l'été, comme montré sur les dessins.

En hiver, à 6h et 18h, le panneau se trouvera dans l'hémisphère obscure (même dessin en plaçant le soleil à gauche).
La durée du jour est presque divisée par deux en hiver pour n'être que d'un peu plus de 8h30 à la latitude de Bordeaux… Il semble que l'expression du cos(θ) ne rende pas compte de cela.
Sur mon exemple les courbes correspondant aux solstices d'été (en rouge) et d'hiver (en vert) se recouvrent parfaitement…



Or, à 6h et 18h, le jour de Noël, il fait nuit, quelle que soit l'inclinaison que je donne à mon panneau…
Ce qui m'intéresse, c'est de comparer les flux solaires reçus en hiver et en été, en fonction de l'inclinaison du panneau…

[gts2]

Bonjour,

Tout ce que vous dites est exact, je ne vois pas trop où est votre problème : pour que le panneau soit éclairé, il faut qu'il fasse jour et que cos \theta soit positif.

[mécano41]

Bonjour,

A tout hasard, je me permets d'intervenir pour te signaler un sujet similaire dans lequel j'ai pu apporter une aide pour la représentation du système. Dans l'appli. on entre les angles d'azimut et de site du panneau dans un rep. Oxyz,( Ox pointant vers le sud) et les angles d'azimut et de site du soleil. On récupère l'angle de la direction du soleil avec le plan du panneau et celui de sa projection sur le panneau avec un axe de celui-ci. On peut faire bouger tout le système pour l'observer sous un angle plus intéressant (voir les indications dans le message)

Les calculs de la feuille visible sont ceux propres à l'utilisation ; les autres concernant la visualisation sont cachés (et avec des lignes cachées) pour éviter de modifier ou effacer des cellules par inadvertance mais il n'y a aucun mot de passe?

Pour le calcul de la direction du soleil à une date et à une heure données, je n'y connais rien...mais peut-être que le demandeur pourra t'informer des calculs qu'il a faits. Les quatre valeurs d'entrée, données par les curseurs du haut, sont celles qu'il a données. Pour l'appli., tu vas directement au message #22 du sujet :

https://forums.futura-sciences.com/m...u-solaire.html


Cordialement

[gts2]

Vous pourriez aussi tenir compte des deux données par rapport au panneau et par rapport au sol qui vous permettrait de tenir compte de l'épaisseur de l'atmosphère, vous auriez alors qqch du genre :

éclairement= dans laquelle permet de calculer l'épaisseur d'atmosphère traversée et f(h) le facteur d'atténuation du à cette traversée.

[gts2]

Une référence pour le "f(h(cos))" : wiki