Identification d'erreur qui donne de mauvaise valeur de g lors d'un TP (pendule conique)

[invite30dc8e8c]

Salutation !

Je suis actuellement face à un problème.
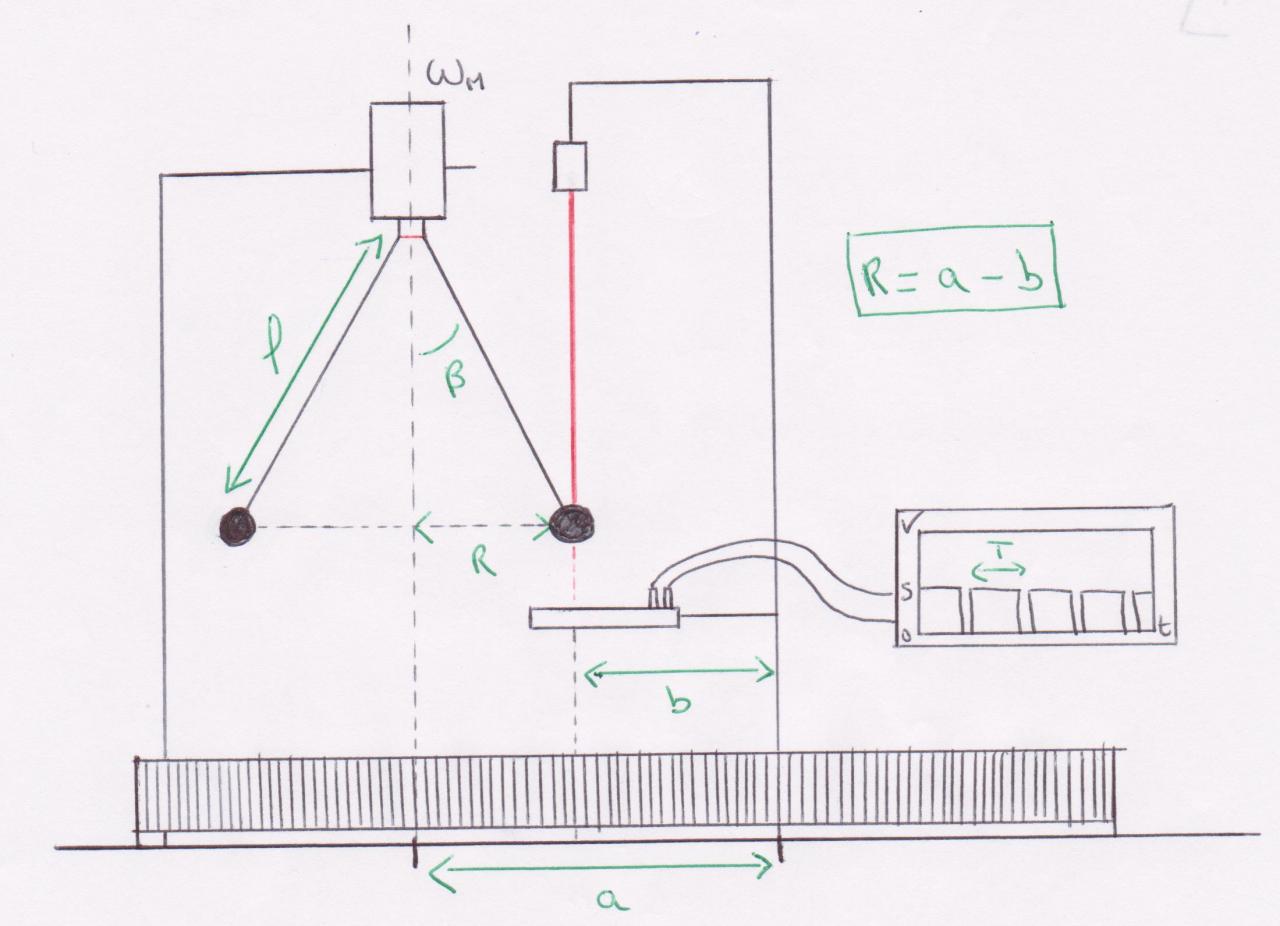
J'ai effectué un TP où le but était de mesurer la valeur de g avec un pendule conique.

Pour cela je mesure le rayon qui correspond à la déviation de la masse avec l'axe de rotation du moteur ainsi que la période de rotation de la masse autour de l'axe du moteur.
Avec l'étude théorique j'obtiens la formule de g = sqrt(l² - R²)*w² et w = (2pi/T)

voici les 3 mesures que j'ai pu effectué (manque de temps, j'avoue que c'est très peu mais je dois refaire le TP vendredi)

R = 11.4 cm et T = 0.648 s ce qui le donne g = 11.85 m.s-²
R = 13.3 cm et T = 0.642 s ce qui le donne g = 10.14 m.s-²
R = 14.6 cm et T = 0.600 s ce qui le donne g = 9.55 m.s-²

Donc j'augmente la vitesse de rotation du moteur pour avoir un R croissant (qui nous donne T décroissant).
Je me suis donc questionner sur les valeurs, relativement éloigné de 9.81 et pourquoi est-ce que j'obtenais des valeurs aussi éloigné pour les faibles rotations.
Pendant la manip j'avais remarqué que la masse tournait autour d'elle-même et que son moment cinétique diminuer avec l'augmentation de la vitesse de rotation du moteur.
J'aimerais donc savoir si ce moment pourrait ralentir ma masse et du coup me donner des valeurs erronées de la période et/ou du rayon ce qui explique un tel écart.
Je n'ai pas établie mon modèle théorique en prenant en compte un quelconque moment, (j'ai assimilé la masse à un point).

Donc est ce qu'un objet qui tourne autour d'un axe voit sa vitesse de rotation ralentir en fonction de sa rotation autour d'elle même ?
J'ai donc essayé de me demander si la rotation de la terre autour d'elle même faisait ralentir sa révolution autour du soleil.

Qu'est ce que vous en pensez ?

Merci d'avance pour vos réponses )


-----

[gts2]

Bonjour,

Pour les mesures, je ne sais trop, il parait quand même bizarre qu'une variation de 16% de R conduise à une variation de 1% de la période : problème de lecture/recopie ...
Que vaut L ?

Pour ce qui est de la théorie, on peut décomposer l'étude d'un solide en le mouvement de G et le mouvement du solide dans le référentiel barycentrique. Votre formule ne fait intervenir que la première étude et est indépendante (au premier ordre) de la rotation. Au premier ordre, car on peut imaginer que le mouvement de rotation induise des forces.

[Resartus]

Bonjour,
Si votre "a" est bien mesuré à partir de l'axe du moteur où s 'attache le pendule, il faut, pour obtenir le bon "R", retirer à "a-b" le rayon de cet axe
(qui, d'après le dessin, semble relativement gros)

Et, par ailleurs, le "l" doit être compté par rapport au centre de gravité de la bille : avez-vous pensé à rajouter le rayon de cette bille à la longueur du fil?

Ces deux décalages pourraient expliquer au moins une partie des erreurs trouvées...

[Black Jack 2]

Bonjour,

Il faut, je pense, tenir compte du fait que la masse n'est pas ponctuelle.

Dans l'exemple qu'un pendule oscillant (ce qui n'est pas le cas ici, juste pour l'exemple)

Si on appelle L la longueur du fil (de masse négligeable) et R le rayon de la bille supposée pleine et homogène de masse m
L étant bien mesuré entre le point d'attache et le centre de la bille ...

La monent d'inertie autour du point fixe est I = m.L² + (2/5).m.R² (et pas mL² comme quand la bille est ponctuelle).

Pour trouver la période d'oscillation, si on considère la masse comme ponctuelle, il faudra donc prendre comme longueur, non pas la vraie longueur du fil, mais une valeur corrigée

Les calculs sur ce sujet peuvent être trouvés sur ce lien : http://www.unine.ch/files/live/sites...mecaniques.pdf

dans le chapitre "expérience n°9"

L'erreur faite en négligeant la "non ponctualité" de la bille augmente évidemment avec le rapport R/L et peut parfois conduire à des erreurs importantes.
***************

Il faudrait refaire une réflexion similaire sur le type de pendule de l'exercice pour voir si cet effet (non ponctualité de la bille) amène ou non des erreurs significatives.

[A voir en vidéo sur Futura]

[gts2]

Calcul fait avec une tige de longueur l avec le centre d'inertie à L du centre de rotation, on obtient un facteur correctif , pour atteindre une erreur de 1% il faut l=0,35L. Au maxi avec une tige entière, on a un facteur correctif de 4/3.

[invite30dc8e8c]

Bonsoir,

Pour mon étude je dois rester dans un cas simple avec la masse étant ponctuel (étant seulement en 2ème année de licence) mais dans le rapport de TP je voudrais apporter une analyse sur le écart que j'obtiens.
En ce qui concerne la longueur je l'ai fixer à l = 17 cm en incluant la longueur de la masse.

Merci pour votre réponse.

[invite30dc8e8c]

Bonsoir,

Pour le dessin il n'est pas du tout à l'échelle, seulement pour que vous aillez une idée de l'installation. J'ai décidé de faire la mesure de R en prenant la différence a - b car ces deux points sont directement sur mon banc de mesure gradué, ce qui améliore la précision des mesures.
Pour la longueur l je la prends en sommant la longueur du fil et la longueur de la masse.

Les masses utilisées sont des cylindres. Donc la barycentre devrait être facile à calculer.
Demain je dois refaire les mesures, je comparerais la différence en prenant en compte ce facteur.

Merci pour réponse.

[invite30dc8e8c]

Bonsoir,

Je compte refaire la mesure en prenant cette fois-ci une valeur de l = longueur du fil + la longueur de masse/2.
La masse utilisé est un cylindre. Qu'en pensez vous ?

Pour ce qui est du rapport longueur de la masse / longueur du fil, pour les mesures effectué il y a un écart relatif de 25%. je dois avouer que c'est assez important.

Le fil avait une longueur de 13.5 cm et la masse cylindrique 3.5 cm. Si on prend la longueur au niveau du centre de gravité de la masse on obtiens une ecart relatif de 13%.

Merci beaucoup pour votre réponse.

[invite30dc8e8c]

Bonsoir,

Lorsque vous parlez de la longueur L c'est la longueur du centre de gravité de la masse jusqu'à l'attache du fil ?

Pour corrigé mes valeurs sur les nouvelles prises de mesures, je vais utilisé la longueur l = longueur du fil + la moitié du cylindre.

Et je vais attendre que la masse se stabilise, elle tourne vite sur elle-même au début puis s'arrête au bout d'un certain temps et j'ai remarqué de le rayon augmentait quand la masse se stabilisait (à vitesse de rotation du moteur constant).

C'est peut être la grosse source d'erreur ?

Merci pour votre réponse.

[gts2]

Vu le rôle de l (calcul du cosinus), l doit aller jusqu'à l'axe (mais là encore c'est peut-être un pb de dessin).
Pour R idem, il faut que votre triangle rectangle {l,R,(l²-R²)} soit bien un triangle rectangle.

[gts2]

Lorsque vous parlez de la longueur L c'est la longueur du centre de gravité de la masse jusqu'à l'attache du fil ?
Pour corrigé mes valeurs sur les nouvelles prises de mesures, je vais utilisé la longueur l = longueur du fil + la moitié du cylindre.

L est la distance entre le centre de gravité et l'intersection du fil avec l'axe de rotation (remarque à cause de votre dessin, peut-être sans conséquence).
Si vous dites que la rotation joue un rôle, il faut attendre la stabilisation en effet.

Deuxième message car celui de 19h57 est arrivé pendant que j'écrivais celui de 20h01

[invite30dc8e8c]

Je vous ferai une conclusion sur le topic pour vous dire si les changements auront eu une conséquence sur le résultat ou pas.

Encore merci pour vos réponse