Ce sont là les paroles d'un grand sage ?Envoyé par pm42
Moins les gens comprennent, plus ils prennent ceux qui leur expliquent de haut.
C'est normal : vu qu'ils ne comprennent pas, les réponses leur paraissent aberrantes
Bonjour le rapport avec le sujet.
Non mais déjà on ne le traite pas en gravité newtonienne vu qu'il a été démontré que la théorie newtonienne est une approximation de la théorie de la relativité.
En plus la théorie de Newton ne suppose rien concernant même l'existence des atomes.
Pourquoi alors s'y référer lorsqu'on parle de relativité, en plus à l'échelle de l'atome, juste pour contredire ?
Ben oui, c'est exactement ce que vous faites.Comme souvent, en mélangeant le tout à coup de phrases, on peut obtenir le résultat qu'on veut et sa théorie perso où les atomes individuels n'exerceraient pas de gravité.
Non il faut rien, c'est pas vous qui allez décider s'il faut vérifier un aspect aussi fondamental, on sait pas mesurer, on a des avis théoriques. Point barre.Effectivement ce n'est pas vérifié expérimentalement à ce niveau (comme beaucoup de choses, c'est l'intérêt d'avoir des théories qu'on peut utiliser sans tout vérifier tout le temps une fois qu'elles sont validées) mais il faudrait expliquer par quel mécanisme cela se produirait et à partir de camp plusieurs atomes eux exerceraient de la gravité.
Qui a dit à part vous qu'il faut reléguer les théories modernes de la gravité derrière "les certitudes de la théorie de Newton" ?....Et pourquoi toutes nos théories de la gravitation seraient fausses malgré leur degré de validation avec une précision énorme.
Je sais pas, si vous le dites.Sinon, on est dans le cas de la théière de Russel.
Dernière modification par ArchoZaure ; 11/03/2023 à 13h42.
Je n'ai pas vu un seul argument physique, juste des affirmations gratuites, du mépris et l'ignorance du la charge de la preuve (cf. la théière de Russel déjà citée).
J'en reviens à ce que je disais : moins les gens savent, plus ils affirment leurs erreurs et théories perso avec cet ton.
Bon courage aux autres.
Le principe d' équivalence masse pesante /masse inerte est dans les équations de Newton ! Vous avez pour 2 masses m1 et m2 F1=GMm1/d2= m1.g1 F2=GMm2/d2= m2.g2 d ' où g1=g2 , les 2 masses m1 et m2 ont la même accélération, et donc vitesse de chute . Alors en fait le m1 ,m2 de droite c'est la masse inerte , quand on écrit f=m.g ,on suppose l' égalité de la masse pesante à gauche avec F=mMG/d2 et la masse inerte ! Mais pour moi, il n' y a rien d' étonnant, ça montre , a priori, que la force de gravitation de Newton est une force comme les autres , car pour une force mécanique comme un ressort, on a bien aussi F=m.a , la différence de la force de gravitation à la Newton, serait que cette dernière s' exerce sur tout les atomes de la masse m , tandis qu' une force mécanique comme un ressort s' exerce , sur une petite surface extérieure de la masse,(la surface poussée) propageant la force par effet"domino" à la vitesse du son dans la masse !
Grenier Roland
Donc d'après vous tout un tas de scientifiques se seraient lancés dans la traque d'une fumeuse théière cosmique ?
Cette idée est tout bonnement ridicule et peut-être un peu de modestie dans votre capacité à évaluer l’intérêt d'une hypothèse en physique serait de mise.
Merci de ne pas nous faire de la morale en nous assénant des généralités de discussion de comptoir.
Restez technique.
Un avis sur la question :
https://blogs.futura-sciences.com/ba...lle-emergente/
Bonjour,
...beaucoup de remarques à faire en ce qui me concerne.
Avant tout, sans savoir si c'est tout-à-fait nécessaire, je voulais juste préciser un point : quand j'écris le marteau attire aussi la terre, cela sous-entend que la terre se déplace aussi vers le marteau, en tous cas théoriquement, mais cela serait bien entendu difficile à mesurer...
est-ce exact ?
merci pour vos références à lire,
bonne journée
Oui , c'est exact , si la Terre attire le marteau , réciproquement le marteau attire la Terre de la même façon ,
mais si vous appliquer F = m a à chacun , vous allez comprendre que la Terre ne va se déplacer qu'assez peu dans l'opération ...
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Oui, mais XK150 a déjà répondu et vous a même donné la marche à suivre pour calculer les déplacements respectifs de la Terre et du marteau. Je vous suggère de faire ce calcul et de comparer le déplacement de la Terre à la taille typique d'un atome ou d'un noyau atomique, par exemple.
Il ne sert à rien de remplir des pages et des pages de vent si on n'est pas capable d'avoir cet ordre de grandeur.
Not only is it not right, it's not even wrong!
...merci pour votre réponse ;
(je garde aussi en tête, que mon approche reste ici très XVIIème siècle pour paraphraser gts2, puisque il s'agit présentement d'une lecture de type newtonienne)...
Salut,
Non, non, XVe siècle. Au XVII les scientifiques faisaient les calculs
(je rigole contrairement à toi, ils calculaient aussi dans l'antiquité, sur le fronton de l'Académie d'Athène il était écrit "que nul n'entre ici s'il n'est géomètre" (les calculs se faisaient par la géométrie à l'époque))
Mais pour l'approche newtonienne, vu les questions, pour l'essentiel on peut rester dans ce cadre. Faudrait être cinglé pour utiliser la RG pour calculer l'attraction entre un marteau et la Terre
Déjà pour calculer / mesurer le déplacement (minuscule) de l'axe de rotation de la terre suite au séisme/ras de marée qui a fait tant de mort dans l'océan indien, on a utilisé la mécanique newtonienne. Et les masses des plaques tectoniques c'est autre chose qu'un marteau.
D'une manière générale je constate que tu as du mal à accepter les réponses. Tu as du mal puisque d'une part tu reviens constamment dessus malgré les réponses et tu reproches aux autres d'oublier des choses.
Donc à un moment donné, rien à faire, on ne pourra plus te répondre. Tu ne peux plus faire qu'une chose : vérifier par toi même.
Déjà plus haut je t'avais dit que c'était facile : des équations très simples (F=ma c'est juste une multiplication, et les multiplications ma foi on apprend ça à l'école primaire, même pas dans le secondaire).
Et je conseille aussi que tu regardes du coté :
- De la troisième loi de Newton (et de sa relation avec la conservation de l'impulsion et dee l'énergie)
- Du principe d'équivalence
Et leurs conséquences.
Et aussi leur vérification (la précision est "sidérante" pour employer les mots d'un physicien que j'ai lu ce matinmême s'il parlait de l'électrodynamique quantique )
C'est facile. Et tu verras que cela répond à toutes tes questions.
Bonne recherche personnelle (et pour éviter 70 messages de plus pour comprendre que lorsque je pisse dans l'urinoir cela ne déplace pas beaucoup la planète) (je trouve ça plus amusant que le marteau
Dernière modification par Deedee81 ; 12/03/2023 à 14h00.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Oui , mais cela , c'est valable en Belgique : nous , en France , on pisse dans les violons ... Ma question : que devient le violon ?lorsque je pisse dans l'urinoir cela ne déplace pas beaucoup la planète) (je trouve ça plus amusant que le marteau
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Salut,
Il se déplaceMa question : que devient le violon ?
Note que c'est quand même mieux que de laisser tomber un marteau sur le violon
Sinon c'est bien vu, se casser la tête sur quelque chose :
- d'aussi simple (avec un strict minimum de connaissance de Newton)
- de trivial à vérifier (une simple multiplication, faut vraiment pas avoir fait Harvard)
- d'impossible à vérifier (en science on s'occupe généralement de ce qu'on sait vérifier
c'est assez hummmm disons bizarre.
Notons que j'ai cité le séisme surtout parce que justement là c'est vérifiable. Plus récent : https://www.maxisciences.com/seisme-..._art13130.html
Mais c'est encore plus intéressant avec la Lune. C'est plus proche de l'idée du marteau et là c'est aisément vérifiable : la Terre tourne autour du centre de gravité commun (qui est un peu sous la surface terrestre mais... pas au centre de la Terre !) sans compter les forces de marées (un marteau aussi en provoque mais c'est impossible à mesurer avec un marteau ou alors il faut un marteau maousse costaud, celui de Thor peut-être
Dernière modification par Deedee81 ; 13/03/2023 à 06h39.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour,
désolé, le plus probable est effectivement, que je ne comprenne finalement rien du tout. Cependant, après avoir lu les différents documents, que vous me donnez en références et sur lesquels il faudra que je revienne sûrement encore et encore pour les assimiler, je relève ceci :
Tout d'abord, en réponse à albanxiii :
je cite Wikipédia, article Lois de mouvement de Newton :
"le cas des actions à distance est également difficile à conceptualiser."
je reprends alors le document cité :
Concernant les forces d'interactions gravitationnelles entre deux objets, il est dit que : "Ces deux forces sont appliquées aux centres des objets, elles ont même direction, des sens contraires et même valeur."
Et donc, je crois pouvoir résumer (dans un premier temps), ce que je ne comprends pas du tout (et pourtant il s'agit du plus basique) :
c'est l'égalité des forces entre deux objets alors même, que vous confirmez, que le marteau exerce finalement une force bien différente sur la terre, que la terre sur le marteau ;
Pouvez-vous éclaircir ce point ?
merci,
bonne journée.
Dernière modification par franklin. ; 21/03/2023 à 12h34.
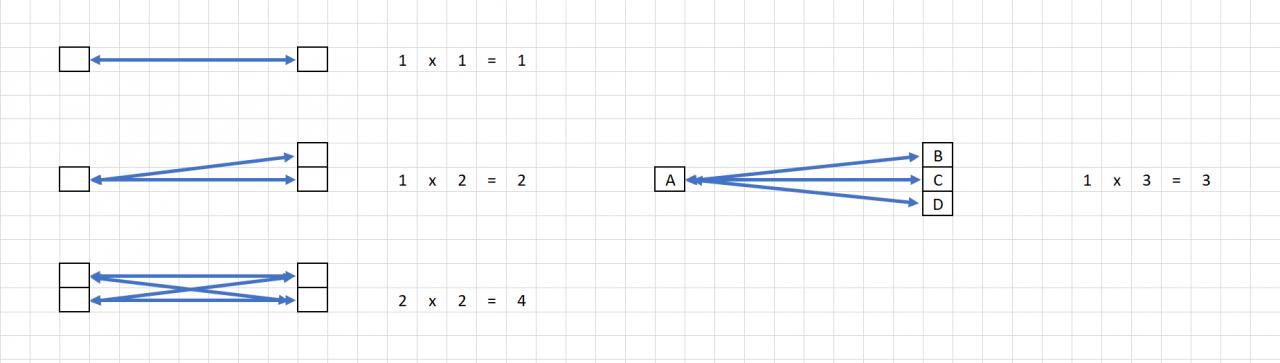
Je prends mon schéma (qui a eu un certain succès) fait pour une autre discussion :
Il suffit de mettre autant de petits cubes pour créer d'un côté un marteau et de l'autre, beaucoup, beaucoup plus pour créer la terre.
A noter que l'on voit bien sur la partie de droite que :
1/ A est attiré par B, C & D et subit donc bien une force d'intensité 3 (unité arbitraire)
2/ B est attiré par A, C est attiré par A et D aussi, donc BCD subit une force d'intensité également de 3.
Mais qu'en triturant F=ma pour extraire a, soit a = F / m, on remarque que :
1/ L'accélération initiale subie par A (masse arbitraire de 1) est de 3 (la force) / 1 (masse) = 3 (unités arbitraire d'accélération)
2/ L'accélération initiale subie par BCD (masse de 3) est de 3 / 3 = 1 (unité arbitraire d'accélération)
(dès qu'il sera validé) :
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Salut,
EDIT croisement mais très complémentaire
Bizarre, il me semblait l'avoir déjà expliqué avec l'histoire de l'abus de langage mais je ne retrouve pas.
Bon ici :
Non, non, c'est toujours égal, voir :
https://fr.wikipedia.org/wiki/Lois_d...-r%C3%A9action
Et non Xk ne dit pas que ces forces sont différentes. Il écrit ceci :
c'est moi qui met en évidence
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
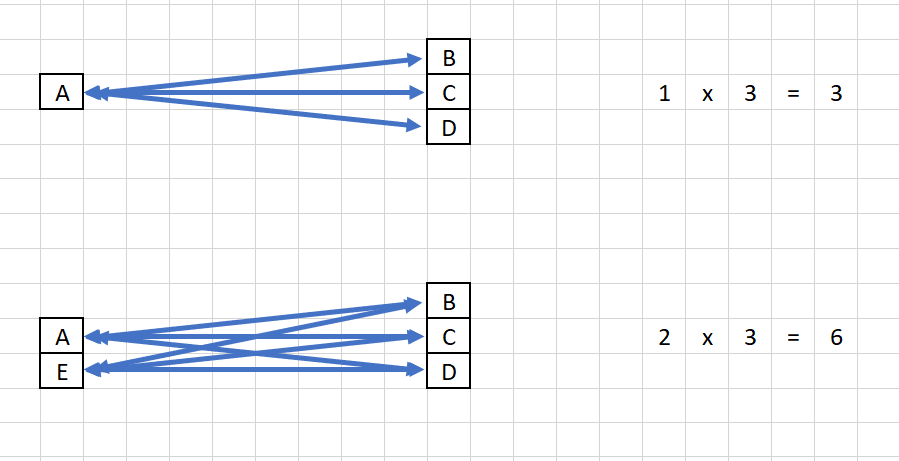
On peut même aller plus en comparant (peut-être pas marteau et plume, mais 1/2 marteau et marteau, ce qui revient au même).
Si A (masse arbitraire 1) est un 1/2 marteau et que AE (masse = 2) est un marteau complet, qu'observe-t-on :
1/ A lorsqu'il est seul, est comme auparavant attiré par une force de 3 (liaison : A-B, A-C, A-D)
2/ AE est cette fois attiré par une force de 6 (A-B, A-C, A-D, E-B, E-C, E-D).
Mais que le plus important est que les accélérations initiales du marteau et du 1/2 marteau sont rigoureusement égales, pourquoi car :
1/ l'accélération initiale de A (lorsqu'il est seul) est de 3/1 = 3 (unité arbitraire)
2/ l'accélération initiale de AE est de ... 6/2 = 3
Autrement dit que l'accélération initiale de A et de AE dépendent bien la masse de la terre, mais pas de leur masse à eux. C'est bien ça, la trouvaille de Newton. Et là, c'est tout à fait rigoureux. Il n'y a pas d'approximation (dans le modèle de Newton).
Par contre, l'accélération initiale de la terre (BCE), elle diffère entre les deux expériences. Dans le premier cas, elle vaut 3/3 = 1 et dans le second 6/3 = 2. Mais ça, Newton le savait.
Mais en première (et même en deuxième, troisième ...) approximation, on peut considérer que cette accélération est nulle (au vu de la masse relative de la terre par rapport à l'attraction engendrée par le marteau ou a fortiori par le 1/2 marteau) et donc que la terre est immobile.
Dernière modification par Sethy ; 21/03/2023 à 15h40.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
L'incompréhension vient peut-être que si, effectivement, les forces sont égales les accélérations, elles, sont très différentes.
Pour être plus clair.
Il en résulte que si l'accélération subie par le marteau est "palpable" (on voit bien la vitesse du marteau changer durant les demi-secondes de sa chute), celle de la Terre est complètement imperceptible.
ça, c'est quand on est immobile par rapport à la terre.
Quand on est à cheval sur le manche du marteau, donc immobile par rapport à celui-ci, il en résulte quoi ? Voit-on alors la vitesse de la terre changer durant les demi-secondes de sa chute ?
Il suffit de faire l'application numérique. m_marteau = 1 kg, a_marteau = 9,81 m/s^2, m_terre = 6x10^24 kg. De là tu peux déduire l'accélération de la terre.
Et comme v = a.t, tu multiplies cette accélération par 1/2 seconde et tu conclus.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Salut,
Tout à fait, d'autant que l'abus de langage que j'ai évoqué (je retrouve plus le message où j'en avais parlé, pfffff) c'est justement ça. Parfois on lit "pousse/attire plus fort" alors que c'est l'accélération qui est différente mais les forces égales.
On comprend très bien que ça peut prêter à confusion
Il y a parfois des noms un peu trompeur en physique ou des expressions, on en a déjà discuté à l'occasion. Mais quand c'est le langage courant qui s'emmêle c'est encore pire (et y en a un paquet comme ça).
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
À proprement parler, ces problèmes de 2 corps en interaction gravitationnelle doivent se résoudre dans le référentiel du centre de masse (cette étape préliminaire est le plus souvent passée sous silence...)
L'idée est alors de se placer au centre de masse et de là d'observer les 2 objets tomber vers celui-ci avec chacun leurs accélérations données dans mon message précédent.
Ici, ce point de vue n'est pas très pratique : vu la position du centre de masse Terre-marteau, difficile de se positionner dessus
Oui, et faut juste préciser que ça découle en mécanique newtonienne de la nécessité de ne pas avoir de référentiel accéléré.
On appelè ça le "référentiel galiléen" ou référentiel inertiel.
https://fr.wikipedia.org/wiki/R%C3%A..._galil%C3%A9enEn physique, un référentiel galiléen (nommé ainsi en hommage à Galilée), ou inertiel, se définit comme un référentiel dans lequel le principe d'inertie (Première loi de Newton) est vérifié, c'est-à-dire que tout corps ponctuel libre (i. e. sur lequel ne s’exerce aucune force ou sur lequel la résultante des forces est nulle) est en mouvement de translation rectiligne uniforme, ou au repos (qui est un cas particulier de mouvement rectiligne uniforme). Par suite, la vitesse du corps est constante (au cours du temps) en direction et en norme.
Une définition, plus abstraite, mais équivalente, est celle d'un référentiel par rapport auquel le temps est uniforme, l'espace homogène et isotropeR 1. Il s'agit en pratique d'une idéalisation, la recherche d'un référentiel inertiel étant un sujet délicat, et sa détermination concrète toujours approximative.
Tout référentiel en mouvement de translation rectiligne et uniforme par rapport à un référentiel galiléen est lui-même galiléen : il existe donc une infinité de référentiels galiléens, les formules de passage de l'un à l'autre se faisant par transformation de Galilée, qui laisse inchangée la forme des lois du mouvement de Newton. En mécanique relativiste, le passage d'un référentiel galiléen à l'autre fait intervenir la transformation de Lorentz, qui se ramène à celle de Galilée pour des vitesses faibles devant celle de la lumière dans le vide.
Les lois de la mécanique sont invariantes par changement de référentiel galiléen : ce postulat constitue le principe de la relativité galiléenne, qui toutefois n'est pas valable pour l'électrodynamique classique. En effet, les formules de passage d'un référentiel galiléen à un autre prévoient une dépendance de la vitesse de la lumière dans le vide c selon le référentiel par composition des vitesses, ce qui n'est pas observé. La prise en compte de cette invariance de c par changement de référentiel galiléen est à la base de la théorie de la relativité restreinteR 2.
Dans un référentiel non inertiel, qui est animé d’un mouvement accéléré par rapport à un référentiel galiléen, il faut faire intervenir les forces d’inertie. Ces forces se distinguent de celles prises en compte dans un référentiel galiléen, car elles ne sont pas associées à une interaction entre le corps dont on étudie le mouvement et un autre corps.
https://fr.wikipedia.org/wiki/Probl%...ticule_fictiveÀ proprement parler, ces problèmes de 2 corps en interaction gravitationnelle doivent se résoudre dans le référentiel du centre de masse (cette étape préliminaire est le plus souvent passée sous silence...)
L'idée est alors de se placer au centre de masse et de là d'observer les 2 objets tomber vers celui-ci avec chacun leurs accélérations données dans mon message précédent.
Ici, ce point de vue n'est pas très pratique : vu la position du centre de masse Terre-marteau, difficile de se positionner dessus
Avec la masse réduite
et la masse totale
On a alors
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
J'avais pensé à une illustration "pratique".
Imaginons l'expérience suivante. On prend un élastique et avec ses deux index, on le met en tension.
Il y a une évidence, c'est qu'il est nécessaire d'appliquer la même force avec les deux index. Si on essaie d'appliquer une plus grande force avec l'un des deux, soit on doit compenser avec l'autre, soit les deux doigts se déplacent. Question égalité des forces, on peut la vérifier à condition que l'élastique soit suffisamment solide et que la traction soit également suffisante. Dans ce cas, au bout d'un moment une "marque" apparaitra sur les doigts et elle sera de même intensité sur les deux index.
La tension de l'élastique est donc une bonne analogie avec la force qui s'exerce dans le cas (par exemple) où on ne considère que 2 blocs (voir mon schéma, discussion #74, 1er situation "1x1"). On est bien d'accord que la même force s'exerce sur les deux index. C'est vraiment équivalent à l'attraction réciproque.
Imaginons maintenant qu'au sol, on a placé 2 bouteilles d'eau minérale (1,5L) mais l'une pleine et l'autre vide. Il est assez évident que si on entoure les deux bouteilles de l'élastique préalablement mis sous tension et qu'on lâche simultanément l'élastique des deux côtés, la bouteille pleine va beaucoup moins bouger que la bouteille vide.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Bonjour,
...et je ne voudrais pas, que ma relative ignorance des mathématiques puisse gâcher le raisonnement, mais j'y pense depuis quelques jours :
la question que je me pose est de savoir si G de l'équation de la gravité universelle ne pourrait pas s'appliquer à chaque masse avec une expression du style : G x M x G x m ?
(je ne suis pas du tout sûr de cette formule mathématique au numérateur de l'équation, mais l'idée que G s'applique aux masses respectives et non, seulement au produit des masses pourrait-elle être une piste à suivre ? )
Cette idée rejoint alors votre proposition, selon laquelle l'accélération s'applique à chaque différente masse pour égaliser les forces (une petite difficulté conceptuelle vient du fait que l'application de G aux différentes masses influence l'accélération de l'autre corps) ;
Dîtes-moi si cela vous semble totalement erroné ou potentiellement correct ?Pour être plus clair
Il en résulte que si l'accélération subie par le marteau est "palpable" (on voit bien la vitesse du marteau changer durant les demi-secondes de sa chute), celle de la Terre est complètement imperceptible.
Sous cet angle ci :
- l'expression mathématique ferait alors dépendre de la masse de chaque objet, la "force" exercée,
- j'ajoute que la masse du marteau, minime par rapport celle de la terre, entraîne, qu'effectivement ne retenir que la force exercée par la terre sur le marteau (que l'accélération du marteau mesure) est une excellente approximation, de l'interaction entre les deux objets,
- en suivant cette logique, il me reste alors à comprendre comment on calcule l'interaction entre deux corps, notamment en astronomie, donc je suis allé lire l'article Wikipédia - Lois de Kepler :
"Les lois de Kepler peuvent s'appliquer simplement dans le cas d'un problème à deux corps, sans la présence d'un objet central prépondérant : dans ce cas (comme d'ailleurs dans le cas général), le point central auxquelles se réfèrent les deux premières lois n'est pas le centre du corps le plus massif, mais le centre de masse (ou barycentre) des objets en interaction."
Ce qui permet notamment de reconsidérer ce centre comme "celui des différentes accélérations".
Puis cela me renvoie à l'article Wikipédia - Problème à deux corps, pour relever cette citation :
"Il convient de remarquer que dans le cas particulier important où l'un des corps a une masse beaucoup plus importante que le second (corps central, généralement une étoile, ou une « grosse » planète), par exemple si m_1 \gg m_2, le centre de masse du système est pratiquement confondu avec ce corps central, et la masse réduite est pratiquement égale à celle de l'autre corps, \mu \simeq m_2. À noter toutefois que pour le mouvement de la Lune, qui dans le système solaire possède la plus forte masse relative d'un satellite par rapport à sa planète (1/81 Mt), cette approximation est relativement peu précise."
Et il s'agit à nouveau d'approximation (ou m1>>m2). Il s'avère d'ailleurs, que ce n'est pas très précis pour des corps dont justement la masse est plus proche, terre et lune par exemple ; je me rends alors compte, que stefjm intervient en ce sens, puisque cette citation est effectivement l'énonciation du concept de masse réduite extraite de l'article Problème à deux corps :
https://fr.wikipedia.org/wiki/Probl%...ticule_fictive
Avec la masse réduite
et la masse totale
On a alors
Enfin, je note au passage, qu'est utilisée dans cette citation la notion de "masse relative" dont coussin a pu au préalable relever la bizarrerie :
Quelle étonnante boucle ?
Qu'en pensez-vous ? Et cette question est très sincèrement ouverte à vos réponses (compte tenu de l'enjeu ou des erreurs que je peux faire).
Merci.
Dernière modification par franklin. ; 23/03/2023 à 17h23.
Cela reviendrait à poser G'=G2, en quoi cela change-t-il quelque chose ?
C'est déjà le cas, découper G en
Pourquoi vouloir à tout prix changer quelque chose qui donne de bons résultats dans la limite connue de la théorie ?
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
On n'a pas fait am stram gram pour savoir comment "employer" G.
G découle de la manière dont "on" (Newton) a déduit la formule bien connue de la loi de gravitation universelle F=GmM/r2 d'après les formules bien définies Fm=mam et FM=MaM
et certaines hypothèses.
La réponse se trouve ici :
http://www.aim.ufr-physique.univ-par...ION/grav5.htmlDans son ouvrage, Newton commence par exposer ses 3 lois du mouvement qui fondent la mécanique. Elles s'énoncent comme suit :
1ère loi :
Tout objet en état de mouvement rectiligne uniforme et soumis à aucune force extérieure, conserve son mouvement, dans un repère galiléen.
Cette loi est la reformulation du principe d'inertie formulé par Galilée. On l'appelle couramment "Le principe d'inertie"
2ème loi :
La relation entre la force (F) appliquée à un corps et son accélération (a, définie comme la dérivée seconde du mouvement par rapport au temps) s'écrit :
F=m a, où m est la masse du corps (F et a sont de vecteurs)
C'est le principe fondamental de la dynamique.
C'est la plus puissante des trois lois, car elle permet de calculer quantitativement le mouvement des corps. De plus, on remarquera que si F=0, alors a=0, on retrouve alors première loi.
C'est aussi une révolution comparée à la physique d'Aristote, qui lui supposait que la force s'exerçant sur un corps est proportionnelle à sa vitesse, et non à son accélération.
3ème loi :
Tout corps soumis à une force exerce en retour une force de même intensité et de direction opposée.
C'est pour cela que l'on tient sur le plancher sans passer au travers !
C'est sur la base de ces trois lois, auxquelles Newton ajoute la force de gravitation qu'il déduit les mouvements des planètes.
5.3 La force de gravitation
Comment écrire cette force ? Tout d'abord, et c'est là le postulat fondamental, elle est en 1/R2 (confirmée par l'expérience de la lune). De plus, on suppose qu'elle est proportionnelle à la masse du corps central, M, car les corps les plus lourds attirent plus fortement les corps les plus faibles. C'est pour cela que la pomme n'a pas beaucoup d'influence sur la Terre car elle l'attire avec trop peu d'intensité.
On peut dans un premier temps écrire la force de gravitation : F= k M/R2 où k reste à déterminer.
Dernière contrainte fondamentale : on a vérifié expérimentalement (avec les expériences de chute des corps faites par Galilée) que l'accélération subie par un corps ne dépend pas de sa masse, c'est pour cela que tous les objets tombent à la même vitesse sur Terre.
Utilisons maintenant la 2ème loi de Newton : F=m a , où m est la masse du corps qui est attiré (la Lune, la Pomme) : On a donc F=ma=k M/R2 => a= kM / mR2.
Cette expression dépend explicitement de m, or on a dit plus haut quel'accélération ne doit pas dépendre de m il faut que k soit proportionnel à m.
On écrit alors k= Gm, où G est la constante de Gravitation universelle.Ainsi, on a : a=GM/R2. La force de gravitation universelle s'exprime finalement ainsi :
Fg= GmM/ R2
G a pu être mesuré expérimentalement, et vaut : 6.67259 10-11 m3 kg-1.s-2
C'est là, la synthèse de mille années de recherches, de controverses et d'affrontements philosophiques qui contrastent avec l'extraordinaire simplicité de cette expression. De quoi donner le vertige. Il n'est pas interdit de rester quelques secondes à la contempler.
Bonsoir,
il ne s'agit pas de tout chambouler, il me semble juste que par simplification, les interactions gravitationnelles sont souvent vues comme un principe d'action, plutôt qu'un principe d'interaction.
Est-ce effectivement possible, lorsqu'il s'agit de l'interaction terre/marteau (vue l'énormité de l'action de la terre, comparée à celle du marteau totalement négligeable), là ou ce serait plus difficile lorsqu'il s'agit de considérer, par exemple l'interaction terre/lune ? (voir dernière phrase de la citation Wikipédia déjà énoncée) :
Puis cela me renvoie à l'article Wikipédia - Problème à deux corps, pour relever cette citation :
"Il convient de remarquer que dans le cas particulier important où l'un des corps a une masse beaucoup plus importante que le second (corps central, généralement une étoile, ou une « grosse » planète), par exemple si m_1 \gg m_2, le centre de masse du système est pratiquement confondu avec ce corps central, et la masse réduite est pratiquement égale à celle de l'autre corps, \mu \simeq m_2. À noter toutefois que pour le mouvement de la Lune, qui dans le système solaire possède la plus forte masse relative d'un satellite par rapport à sa planète (1/81 Mt), cette approximation est relativement peu précise."
Les accélérations des objets sont, comme vous le mettez en évidence archozaure, pourtant différentes :
on a Fm=am et FM=MAM.
Est-ce que je fais erreur ?
Merci.
