Bonjour, je suis en L1 physique et j'ai un DM à rendre dans pas longtemps mais je me sens totalement dépassé par cette matière ...
J'espère que vous pourrez peut être m'aider
Merci d'avance !!
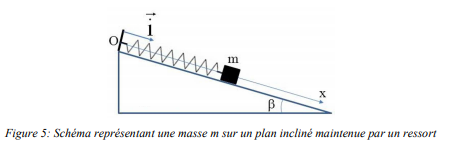
Soit un objet, assimilé à un point matériel, de masse m, et assujetti à se déplacer sur un plan incliné faisant un angle β avec l'horizontale. L'objet est attaché à un ressort à spires non jointives, de raideur k et de longueur à vide ℓ. L'axe Ox est orienté vers le bas et a pour origine O, l'extrémité fixe du ressort (voir figure 1).
Figure 5: Schéma représentant une masse m sur un plan incliné maintenue par un ressort
On se place tout d'abord dans le cas où les forces de frottement sont négligées.
1) Faire un schéma sur lequel vous ferez apparaître les forces s'exerçant sur l'objet lorsque le ressort est en extension, c'est-à-dire lorsque ℓ(t), la longueur du ressort à un instant t, est supérieure à ℓ0
.
2) Déterminer la position d'équilibre ℓe en fonction de m, g, k, β et ℓ0 .
3) Etude du mouvement sans frottement
a. Etablir l'équation différentielle du mouvement. On posera x(t) = ℓ(t) − ℓe pour obtenir une équation différentielle homogène.
b. A t=0, on écarte l'objet de 5 cm par rapport à sa position d'équilibre et on le lâche sans vitesse initiale. Déterminer l'expression de x(t). Déterminer la pulsation propre ω0 et la période propre T0 en fonction de k et m.
4) Etude du mouvement avec frottement fluide
Le montage est maintenant entièrement plongé dans un fluide visqueux, et l'objet est désormais soumis à une force de frottement proportionnelle et opposée à la vitesse telle que: f(vecteur) = −αv.
a. Etablir la nouvelle équation différentielle du mouvement en ℓ(t) puis en x(t). Montrer que cette nouvelle équation se met sous la forme canonique : ¨x(t) + 2lambda x'(t) + ω0²x(t) = 0. Donner l'expression de λ en fonction de α et m.
b. On souhaite que l'objet s'arrête à sa position d'équilibre le plus rapidement possible. Dans ces conditions, donner l'expression du coefficient de frottement α = αc en fonction de k et de m. Comment appelle-t-on ce type de mouvement ?
c. Dans le cas où α = αc, déterminer l'expression de x(t) sachant qu'à t=0s, on écarte l'objet de 5 cm par rapport à sa position d'équilibre et on le lâche sans vitesse initiale.
d. Que se passe-t-il si α < αc et si α > αc ? Décrire le mouvement et préciser le nom du régime ainsi que la forme générale de x(t) dans chaque cas.
Voila, encore merci à ceux qui pourront aider !
-----


