Longueur d'une trajectoire suivant équations paramétriques

[ChinoisFou]

Bonjour à tous,

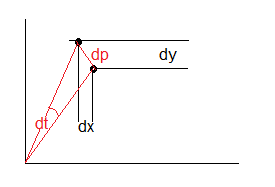
Je fais face à un exercice de méca qui me laisse pas mal perplexe : quelle est la longueur d'une trajectoire décrite par les équations paramétriques x(t)=cos(t)^3 et y(t)=sin(t)^3

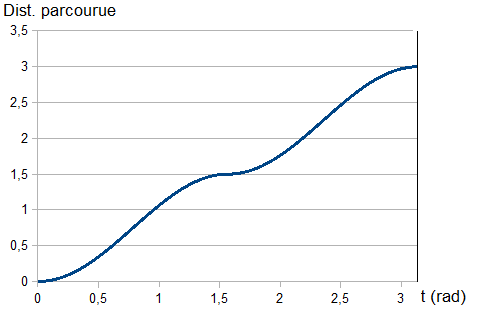
J'ai utilisé WolfRamAlpha pour tenter de visualiser un peu mieux la situation et voilà ce que ça me donne : (ICI)

De ce que je vois, la trajectoire à une longueur simplement de 2pi, car elle forme un cercle de rayon 1. Mais finalement, je n'ai aucune idée de comment le prouver...

Si cela peut aider, nous sommes actuellement au sein du chapitre sur la cinématique du point, mais une fois de plus, je ne vois vraiment pas comment et où je pourrais appliquer les formules que j'ai appris (que ce soit au niveau du mouvement ou de l'énergie...)

Merci d'avance de votre aide, passez une excellente journée !
-----

[Black Jack 2]

Bonjour,

L'équation de la trajectoire est donnée sous forme paramétrique (paramètre t).
Si on veut calculer la longueur d'un "tour" complet, on peut n'en calculer qu'un quart (symétries) et multiplier par 4

On a alors :

x = cos³(t)
y = sin³(t)

x'(t) = ...
y'(t) = ...



Ce qui est sans réelle difficulté.

[ChinoisFou]

Ahh, je comprends mieux ! Merci énormément !

Je trouve donc 3sin(x)cos(x), que j'intègre sur 0 --> pi/2, donc 6 unités de longueur au total? C'est bien ça?

[gts2]

J'ai utilisé WolfRamAlpha pour tenter de visualiser un peu mieux la situation.
De ce que je vois, la trajectoire forme un cercle de rayon 1

Je trouve que cela ne ressemble pas vraiment à un cercle.

[A voir en vidéo sur Futura]

[harmoniciste]

Bonjour,
Pour un angle donné t les coordonnées x étant y étant connues, une infime variation dt de cet angle déplace votre point d'une distance dp telle que dp = (dx² + dy²)^1/2

Le parcours total entre deux valeurs de l'angle t s'obtiendra ensuite en intégrant cette distance.

[phys4]

Je trouve donc 3sin(x)cos(x), que j'intègre sur 0 --> pi/2, donc 6 unités de longueur au total? C'est bien ça?

Cela parait correct, pour cette étoile à 4 branches.

[ChinoisFou]

Je trouve que cela ne ressemble pas vraiment à un cercle.

Oui mais si on "inverse" l'étoile, de sorte à faire "ressortir" l'arc de cercle j'avais l'impression que cela formait une espèce de cercle (mais en effet je me suis TRES mal exprimé).

[ChinoisFou]

Bonjour,
Pour un angle donné t les coordonnées x étant y étant connues, une infime variation dt de cet angle déplace votre point d'une distance dp telle que dp = (dx2 + dy2)1/2

Merci pour cette explication théorique de la formule ! J'ai appliqué bêtement sans réellement comprendre, et l'explication est très claire, merci encore !

[harmoniciste]

De ce que je vois, la trajectoire à une longueur simplement de 2pi, car elle forme un cercle de rayon 1.

Comme l'a dit gts2, la trajectoire n'est pas circulaire, puisque la distance n'est pas proportionnelle à l'angle t:

[Black Jack 2]

Ahh, je comprends mieux ! Merci énormément !

Je trouve donc 3sin(x)cos(x), que j'intègre sur 0 --> pi/2, donc 6 unités de longueur au total? C'est bien ça?

Pour moi, c'est bien cela pour le total (6 unités).
Cela correspond aux 4 portions d'arc. (Ton "3sin(x)cos(x), que j'intègre sur 0 --> pi/2" vaut 1,5 et correspond à 1 seul des arcs).

[harmoniciste]

C'est bien aussi ce que montre mon graphique: 1.5 unités pour pi/2, 3 unités pour pi, 6 unités pour 2pi , etc...