Ordre de grandeur...contradiction?!

[mehdi97]

Bonjour tout le monde

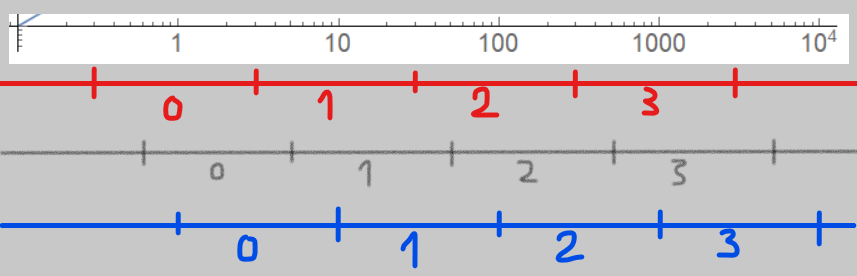
l'ordre de grandeur d'un nombre est défini comme étant la puissance de 10 la plus proche de ce nombre.

on trouve ce qui suit dans plusieurs cours:

"Pour trouver l'ordre de grandeur d'un nombre on doit l'écrire en notation scientifique qui se compose d'un nombre a multiplier par 10^n c'est à dire(a.10^n) . Puis on appliqué la règle suivante:
-Si le nombre a >= 5 , l'ordre de grandeur du nombre est : 10^(n+1)
-Si le nombre a <5 , l'ordre de grandeur du nombre est : 10^n

Prenons le nombre N=50, on a 10^1<50<10^2 et on voit que 50 est plus proche à 10 que à 10^2 (Car 50-10=40 alors que 100-50=50)
Donc d'après la définition: l'ordre de grandeur de nombre N=50 est 10.

mais si on utilise la règle ci-dessus, on trouve que 50=5*10^1 et puisque 5>=5 alors l'ordre de grandeur de nombre N=50 est 10^(1+1)=10^2

Est ce que la règle, utilisée dans plusieurs cours, est fausse?
-----

[gts2]

Bonjour,

Au vu de la définition de l'ordre de grandeur, la comparaison se fait en rapport et pas en différence.

50/10=5 à comparer à 50/100=1/2 : un facteur 2 est bien plus petit qu'un facteur 5.

Ceci étant, donner une définition exacte d'un ordre de grandeur me parait en contradiction avec la notion même d'ordre de grandeur.

[mehdi97]

Merci pour votre réponse.

[mehdi97]

Prenons N=40

Si on applique " la comparaison se fait en rapport et pas en différence ", on trouve:

40/10=4 à comparer à 40/100=1/2,5 : un facteur 2,5 est bien plus petit qu'un facteur 4. Donc
40 est plus proche à 100 que à 10, l'ordre de grandeur de 40 est 10^2 (1)

Cependant, si on applique "Pour trouver l'ordre de grandeur d'un nombre on doit l'écrire en notation scientifique qui se compose d'un nombre a multiplier par 10^n c'est à dire(a.10^n) . Puis on appliqué la règle suivante:
-Si le nombre a >= 5 , l'ordre de grandeur du nombre est : 10^(n+1)
-Si le nombre a <5 , l'ordre de grandeur du nombre est : 10^n"

on trouve 40= 4.10 et 4<5 donc l'ordre de grandeur de 40 est 10 (2)

une autre contradiction entre (1) et (2)

[A voir en vidéo sur Futura]

[gts2]

40 est bien d'ordre de grandeur 100.

Votre définition avec comparaison de a à 5 dans a.10ⁿ parait donc peu adéquate.

Mais, comme déjà dit, donner une définition précise d'un ordre de grandeur est contradictoire avec la notion même d'ordre de grandeur.

Donc à mon avis, ne vous focaliser pas là dessus.

[Sethy]

J'abonde dans le sens de gts2, mais s'il faut vraiment une limite, pourquoi ne pas la calculer ?

Quel est le nombre tel que 10 / a = a / 1 ? Le calcul est simple, a vaut "évidemment" racine (10), soit en environ 3,2.

Et on ne sera "évidemment" pas surpris que log(3,2) = log(racine(10)) = 1/2 . log(10) = 1/2 . 1 = 1/2.

[mehdi97]

notre problème ce n'est pas de trouver une limite. on a un concept qui s'utilise mais où la définition? soit la règle ci-dessus ou la limite que vous trouvez, est-ce qu'il y a un accord universelle sur une seule chose? à la fin, il est possible que la parole de gts2 soit juste: "donner une définition précise d'un ordre de grandeur est contradictoire avec la notion même d'ordre de grandeur".

[gts2]

Bonjour,

Ne vous mettez par martel en tête :

ordre_de_grandeur

wikipedia anglais donne trois définitions (dont en premier celle de @Sethy !).

[coussin]

...

Oui, c'est la raison du fameux 3 dB pour tout ce qui implique des échelles logarithmiques (comme les Bell...) pour vouloir dire un facteur 2.
Enfin, justement c'est pas un facteur 2... Bref, vous voyez ce que je veux dire

[coussin]

Bonjour,

Ne vous mettez par martel en tête :

ordre_de_grandeur

wikipedia anglais donne trois définitions (dont en premier celle de @Sethy !).

Sans y avoir vraiment réfléchi avant, je me rends compte que j'utilise encore une autre définition : pour moi, un ordre de grandeur de 2 va de 100 à 999 et basta

[stefjm]

L'ordre de grandeur est lié à la base et personne n'impose la base 10.
2 est courant avec les dB/octave des électroniciens.
3 est optimale.

[coussin]

Voilà les différentes définitions en relation avec une échelle logarithmique. À vous de voir ce qui vous semble le plus naturel.
De haut en bas, Sethy, wikipedia et moi