Point d'équigravité

[coussin]

Mais pourquoi, si l'on veut obtenir un champ gravitationnel, doit on multiplier G*(Masse/d^2) par le vecteur unitaire?

Pour en faire un vecteur. Vous savez peut-être qu'un vecteur possède une "longueur" et une direction (c'est une "flèche"). G*(Masse/d^2) c'est la longueur. Le vecteur unitaire c'est la direction.
-----

[Tengri]

Pour en faire un vecteur. Vous savez peut-être qu'un vecteur possède une "longueur" et une direction (c'est une "flèche"). G*(Masse/d^2) c'est la longueur. Le vecteur unitaire c'est la direction.

j'ai compris

[Opabinia]

Un vecteur (objet géométrique plus complexe qu'une simple donnée numérique, donc contenant plus d'information) s'exprime forcément en fonction d'un autre (au moins); si l'on écrit par exemple

g = a.u ,

cela implique:
1) que les vecteurs en cause (g, u) ont même direction et sont portés par des droites parallèles, éventuellement confondues;
2) qu'ils sont de même sens si (a) est positif, de sens opposés dans le cas contraire;
3) que leurs normes vérifient ║g║ = │a│*║u║ , soit en notation simplifiée: g = │a│*u = │a│ (puisque u vaut 1 par définition).

[le_STI]

Oui ça me pose problème ça: je suis pas sur de bien interpréter le "à quelles conditions" (au pluriel d'ailleurs...)

Formulé comme ça je n'ai pas l'impression qu'un calcul soit attendu. Pourtant tout porte à croire que si vu que l'énoncé prend la peine de fournir les masses des planètes!

La réponse t'est donnée à la fin du message 16

[Tengri]

Si on s'exprime en termes de valeurs absolues, g.(astre)=G(m/d^2), tant qu'on ne fait pas intervenir de vecteurs, est équivalent à une distance?

Et c'est juste la multiplication par le vecteur unitaire qui transforme la valeur absolue g.(astre) en son équivalent en vecteur force?

J'ai bien compris?

[Opabinia]

Et c'est juste la multiplication par le vecteur unitaire qui transforme la valeur absolue g.(astre) en son équivalent en vecteur force?

Non: on peut avoir g = a.u , (a) représentant un réel positif ou négatif (revoir ce qui précède).
La valeur absolue de (a) n'intervient qu'au niveau de la norme: g = │a│*u = │a│ , par définition positive ou nulle..

Il te faut impérativement maîtriser les notions de base du calcul vectoriel (norme, composante, produit scalaire) si tu veux parvenir à un minimum d'autonomie dans ce domaine.

[Tengri]

Oui : je confondais norme et valeur absolue!

Et encore, ce n'était pas la seule question de l'exercice.

En se référant à la carte du tout début, il était noté :

La carte de champ gravitationnel représente quelques lignes de champ créées par la terre et la lune.

Quel astre déforme le plus les lignes de champ gravitationnel de l'autre astre? Justifier en comparant les valeurs des masses.

Je réponds: La terre concentre plus de lignes de champ gravitationnel que la lune donc elle comprime et réduit les ligne de champ de cette dernière. Le fait que la terre soit nettement plus massive que la lune est la cause du phénomène.

-------

Identifier la ligne de champ sur laquelle sur laquelle se trouve le point d'équigravité, point où les vecteurs champs gravitationnels lunaire et terrestre se compensent.

Je réponds : La ligne du point d'équigravité est la droite (TL) reliant les deux astres


Est ce bon?

[Opabinia]

La terre concentre plus de lignes de champ gravitationnel que la lune donc elle comprime et réduit les ligne de champ de cette dernière.
Dénombrer les lignes de champ paraît délicat, car on peut en tracer à volonté.
Disons qu'à distances comparables la Terre crée un champ gravitationnel beaucoup plus fort que celui de la Lune, parce que sa masse est beaucoup plus élevée.
Ou que le domaine de prédominance du champ gravitationnel terrestre, défini par l'inégalité des normes (g_T > g_L) est beaucuop plus étendu que celui de son satellite.

Il est vrai que le texte de la question
Quel astre déforme le plus les lignes de champ gravitationnel de l'autre astre?
est plutôt sournois en ce qui incite à comparer les déformations des champs des 2 astres, initialement isolés est sans influences mutuelles - difficulté mal cernée et hors de portée des débutants.

Le fait que la terre soit nettement plus massive que la lune est la cause du phénomène.
Exact.

La ligne du point d'équigravité est la droite (TL) reliant les deux astres
Exact.

[Opabinia]

L'inégalité gSUV]T[/SUB] > G_L devient : M_T/TM² > M_L/LM² , soit:

(TM/LM) < (M_T/M_L)^1/2 = 8.99

d'après les données initiales: Masse.T=5.98E24 kg Masse.L=7.4E22 kg

[gts2]

Oui : je confondais norme et valeur absolue !

La valeur absolue est une norme.

[Tengri]

L'inégalité gSUV]T[/SUB] > G_L devient : M_T/TM² > M_L/LM² , soit:

(TM/LM) < (M_T/M_L)^1/2 = 8.99

d'après les données initiales: Masse.T=5.98E24 kg Masse.L=7.4E22 kg

Quelle est cette notation avec puissance 1/2?

Et 8.99 est ici sans unité? Il me semble l'avoir déjà vu au cours de lectures, c'est pas une constante?

[Tengri]

La valeur absolue est une norme.

Mais la réciproque n'étant pas vraie je dois faire la distinction entre les deux notions.

[gts2]

Quelle est cette notation avec puissance 1/2 ?

C'est la racine, la fonction inverse du carré.

Et 8.99 est ici sans unité ?

C'est un rapport de deux grandeurs identiques donc sans dimension

dois faire la distinction entre les deux notions.

Oui, tout à fait

[Tengri]

C'est la racine, la fonction inverse du carré.
C'est un rapport de deux grandeurs identiques donc sans dimension
Oui, tout à fait

J'ai trouvé l'exercice dans un livre de première S.

Les élèves sont censés écrire l'inégalité sous la deuxième forme ?

De toute façon la première forme suffit pour constater et expliquer ce que l'énoncé nous demande... On ne demande pas explicitement ce rapport de masse.


--------

Cette carte des champs gravitationnels appelle peut être d'autres commentaires:

On devine à gauche et hors-champs la présence du soleil. S'il n’ont pas tracé les lignes de champ entre le soleil et la Terre, c'est sans doute dû au fait que le champ gravitationnel solaire est nettement plus important que celui de la Terre

En revanche : beaucoup de lignes entre T et L vu que là c'est le champ gravitationnel terrestre qui domine.

Mais il me semble qu'il n'aurait pas été faux, sur (TL) de mettre une flèche de plus, allant vers L cette fois , vu qu'il y en a déjà une qui va vers T. Juste pour montrer que M sera au centre de gravité, avec annulation des forces.

[Black Jack 2]

J'ai trouvé l'exercice dans un livre de première S.

Les élèves sont censés écrire l'inégalité sous la deuxième forme ?

De toute façon la première forme suffit pour constater et expliquer ce que l'énoncé nous demande... On ne demande pas explicitement ce rapport de masse.


--------

Cette carte des champs gravitationnels appelle peut être d'autres commentaires:

On devine à gauche et hors-champs la présence du soleil. S'il n’ont pas tracé les lignes de champ entre le soleil et la Terre, c'est sans doute dû au fait que le champ gravitationnel solaire est nettement plus important que celui de la Terre

En revanche : beaucoup de lignes entre T et L vu que là c'est le champ gravitationnel terrestre qui domine.

Mais il me semble qu'il n'aurait pas été faux, sur (TL) de mettre une flèche de plus, allant vers L cette fois , vu qu'il y en a déjà une qui va vers T. Juste pour montrer que M sera au centre de gravité, avec annulation des forces.

Bonjour,

Sans préciser l'endroit où le clamp gravitationnel du au Soleil est considéré, cela ne veut rien dire.

Si on considère par exemple le champ gravitationnel du à la Terre sur la lune, on trouve (en norme) : G.Mterre/d² avec d la distance Terre Lune.
et si on considère par exemple le champ gravitationnel du au Soleil sur la lune, on trouve (en norme) : G.Msoleil/d'² avec d' la distance Soleil Lune.

Et avec Mterre = 6.10^24 kg , Msoleil = 2.10^30 kg, d = 384.10^6 m et d' = 150.10^9 m, je te laisse calculer les 2 valeurs de champ ...
et constater que ton affirmation est fausse dans cet exemple.

[Opabinia]

Mais il me semble qu'il n'aurait pas été faux, sur (TL) de mettre une flèche de plus, allant vers L cette fois , vu qu'il y en a déjà une qui va vers T. Juste pour montrer que M sera au centre de gravité, avec annulation des forces.

La position du barycentre (G) du couple Terre-Lune est donnée par la relation:

M_T*TG = M_L*LG

tandis que celle du point d'isogravité (M) vérifie:

M_T/TG² = M_L/LG²

;
Il s'agit de deux points géométriques radicalement distincts, puisque le barycentre est beaucoup plus proche de la Terre, le corps de plus grande masse.

On a en effet:

TG/LG = M_L/M_T = (7.4E²²/5.98E24 kg) = 0.01237

alors que pour le point précédent, le rapport correspondant était:

TM/LM = (M_T/M_L)^1/2 = 8.99

en partant des données initiales: Masse.T= 5.98E24 kg ; Masse.L=7.4E22 kg .

La notion de barycentre est ici inutile, car elle concerne des problèmes de dynamique comme par exemple la rotation du satellite autour de la planète.
La position particulière (T) dont il est ici question est un simple problème de statique, la recherche du point d'annulation du champ résultant créé par deux corps ponctuels.

[Archi3]

La notion de barycentre est ici inutile, car elle concerne des problèmes de dynamique comme par exemple la rotation du satellite autour de la planète.
La position particulière (T) dont il est ici question est un simple problème de statique, la recherche du point d'annulation du champ résultant créé par deux corps ponctuels.

certes mais comme je disais, la Terre et la Lune n'étant pas statiques, le calcul est tout à fait théorique et ne correspond à aucune réalité concrète. Le point de stabilité relative (immobile dans le référentiel tournant), un des points de Lagrange, doit se déterminer en tenant compte aussi de la force centrifuge dans le référentiel tournant.

[Opabinia]

Deux remarques concernant les points mentionnés:

1) Compte tenu des valeurs du rayon terrestre (R_T = 6371 km) et de la distance moyenne Terre-Lune (TL = 384.4E³ km), le barycentre (G) est situé à l'intérieur de la planète; on a en effet:

TG = TL/(1 + LG/TG) = TL/(1 + M_T/M_L) = Tl*M_L/(M_L + M_T) = 384400*7.4E²²/(7.4E²² + 5.98E²⁴) = 4699 km ,

d'où: TG < R_T .

2) Dans la zone du champ gravitationnel produit par les deux corps, le point (M) apparaît comme un point singulier où le champ résultant (g = g_L + g_T) s'annule localement, et où de plus les lignes de champ changent brutalement de direction, en s'y rejoignant à angle droit.

[Opabinia]

certes mais comme je disais, la Terre et la Lune n'étant pas statiques, le calcul est tout à fait théorique et ne correspond à aucune réalité concrète. Le point de stabilité relative (immobile dans le référentiel tournant), un des points de Lagrange, doit se déterminer en tenant compte aussi de la force centrifuge dans le référentiel tournant.

Le problème n'est pas de discuter de la réalité concrète de l'énoncé, mais de répondre aussi clairement que possible aux demandes du primo-posteur.

La localisation des points de Lagrange est strictement hors sujet, et il est pour le moins inapproprié (pour de pas dire déplacé) d'évoquer des problèmes de niveau (bac + 2) vis à vis d'un tiers qui maîtrise à peine des outils enseignés au lycée.

Enfin la notion de force centrifuge n'apporte pas le meilleur moyen de traiter ce genre de question.

[Opabinia]

Mais il me semble qu'il n'aurait pas été faux, sur (TL) de mettre une flèche de plus, allant vers L cette fois , vu qu'il y en a déjà une qui va vers T. ...

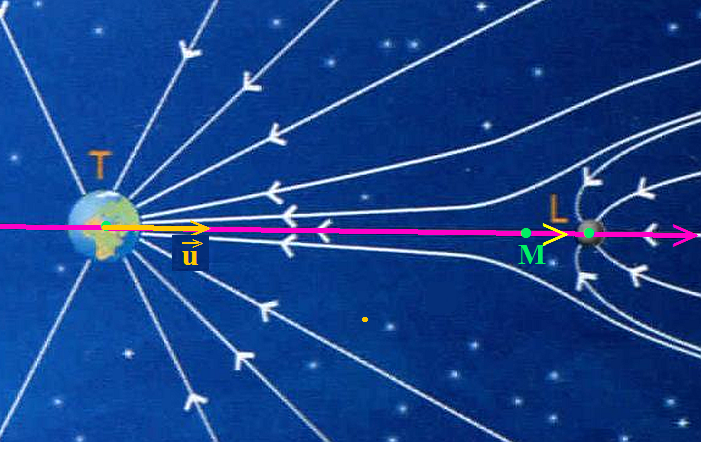
Remarque pertinente .... mais ce qui suit est faux:

... Juste pour montrer que M sera au centre de gravité, avec annulation des forces.

La singularité du point (M) n'en fait pas le barycentre du système Terre-lune (voir ce qui précède).

[Tengri]

Bonjour,

Sans préciser l'endroit où le clamp gravitationnel du au Soleil est considéré, cela ne veut rien dire.

Si on considère par exemple le champ gravitationnel du à la Terre sur la lune, on trouve (en norme) : G.Mterre/d² avec d la distance Terre Lune.
et si on considère par exemple le champ gravitationnel du au Soleil sur la lune, on trouve (en norme) : G.Msoleil/d'² avec d' la distance Soleil Lune.

Et avec Mterre = 6.10^24 kg , Msoleil = 2.10^30 kg, d = 384.10^6 m et d' = 150.10^9 m, je te laisse calculer les 2 valeurs de champ ...
et constater que ton affirmation est fausse dans cet exemple.

J'ai calculé:

Pour T=>L je trouve E18

Pour S=>L je trouve 9.3E26

Donc je comprends qu'il n'y a pas de sens à parler de champ gravitationnel dans l'absolu, c'est toujours une réalité locale, à savoir un champ de tel objet sur un autre.

Par contre là:

L'inégalité gSUV]T[/SUB] > G_L devient : M_T/TM² > M_L/LM² , soit:

(TM/LM) < (M_T/M_L)^1/2 = 8.99

Je ne sais pas comment utiliser cette notation avec l'inverse de la fonction carré et puissance 1/2, c'est peut être un outil qui est vu en maths en parallèle la même année.

Mais peut être que l'énoncé ne l'exige pas pour répondre à l’essentiel...

Je ne sais pas comment utiliser cette notation avec l'inverse de la fonction carré et la puissance 1/2. Peut être s'agit il d'un outil mathématique vu en maths en parallèle la même année.

L'exercice exige d'utiliser cette notation?

[gts2]

Pour T=>L je trouve E18 Pour S=>L je trouve 9.3E26

Il y a des problèmes de puissance de 10 et G a probablement été oublié.

Je ne sais pas comment utiliser cette notation avec l'inverse de la fonction carré et la puissance 1/2. Peut être s'agit il d'un outil mathématique vu en maths en parallèle la même année.

La puissance 1/2 est juste une notation de la fonction réciproque de la puissance 2 (peut-être vue en première), mais on peut aussi la noter et là cela est vu au collège.

[Opabinia]

J'ai calculé:

Pour T=>L je trouve E18
Pour S=>L je trouve 9.3E26

Donc je comprends qu'il n'y a pas de sens à parler de champ gravitationnel dans l'absolu, c'est toujours une réalité locale, à savoir un champ de tel objet sur un autre.

Le sens de ton calcul m'échappe, de même que celui de tes remarques. Et il n'est pas facile de répondre simplement au sujet de l'influence du Soleil, en soi hors sujet.

La norme de la force d'attraction exercée par le Soleil sur la Lune (F_SL) n'est nullement négligeable devant celle de la force exercée par ta Terre (F_TL); elles sont en effet dans le rapport:

r = F_SL/F_TL = (G*M_SM_L/D_SL²)/(G*M_TM_L/D_TL² = (M_S/M_T)(D_TL/D_SL)² =
(1.988E³⁰/5.974E²⁴)(384.4E⁶/149.6E⁹)² = 2.197 .

Cependant, dans un repère tournant accompagnant le mouvement de révolution du barycentre du couple Terre-Lune autour de l'étoile, la force d'attraction exercée par cette dernière peut être négligée, la période du mouvement orbital de la Lune (T_L = 27,32 j) étant nettement inférieure à celle du mouvement autour du Soleil (365.25 j); ce qui justifie de laisser de côté l'influence de ce dernier.

Il s'agit de considérations de dynamique, auxquelles il serait très difficile de répondre et qui sont encore une fois hors sujet: double et prudente raison de ne pas s'y engager.

Je ne sais pas comment utiliser cette notation avec l'inverse de la fonction carré et la puissance 1/2. Peut être s'agit il d'un outil mathématique vu en maths en parallèle la même année.

L'exercice exige d'utiliser cette notation?

gts2 t'a indiqué les deux notations équivalentes. Pour l'exécution des calculs, on peut rentrer dans une calculatrice scientifique les données numériques, telles qu'elles sont écrites.

[Tengri]

Je crois que j'ai bien intégré G aux deux pourtant

Pour TL c'est :

(6.67E-11)*6.10E24/384.10E6

1.059E18, que j'ai eu la mauvaise idée de vouloir arrondir en E18, ce qui m'a au final l'air très faux ...

Pour SL c'est:

(6.67E-11)* 2.10E30/150.10E9

Je trouve bien par contre 9.332E26

[gts2]

Il manque le carré aux distances.

[Tengri]

Ah merci, décidément mes problèmes de concentration ne m'aident pas trop à me replonger dans la physique...

[Tengri]

Bonjour,

En relisant cette conversation , je bute sur ceci:

Bonjour,

Sans préciser l'endroit où le clamp gravitationnel du au Soleil est considéré, cela ne veut rien dire.

Si on considère par exemple le champ gravitationnel du à la Terre sur la lune, on trouve (en norme) : G.Mterre/d² avec d la distance Terre Lune.
et si on considère par exemple le champ gravitationnel du au Soleil sur la lune, on trouve (en norme) : G.Msoleil/d'² avec d' la distance Soleil Lune.

Et avec Mterre = 6.10^24 kg , Msoleil = 2.10^30 kg, d = 384.10^6 m et d' = 150.10^9 m, je te laisse calculer les 2 valeurs de champ ...
et constater que ton affirmation est fausse dans cet exemple.

Dans ce que j'ai mis en gras pourquoi n'y a t il pas normalement au niveau du numérateur, deux masses au lieu d'une seule? Dans le premier cas ne faut il pas mettre le produit Terre-Lune, et dans le second le produit Soleil-Lune?

Ou alors les situations où l'on trouve le produit de deux masses en numérateur c'est juste lorsque les corps sont au voisinage de la Terre?

merci à vous!

[gts2]

Bonjour,

Vous confondez la force gravitationnelle F entre deux objets (1,2) qui fait intervenir le produit des deux masses (m₁ x m₂) et la champ gravitationnel créé par un objet (1) en un point M, noté g, qui ne fait intervenir que la masse de l'objet (m₁). Si on place un objet (2) en ce point, la force subie par (2) est m₂ g et on retrouve bien le produit des deux masses.