Point d'équigravité

[Tengri]

Bonjour,

Après avoir lu le cours d'un manuel j'ai essayé de faire cet exercice dont voici la représentation de l'énoncé:

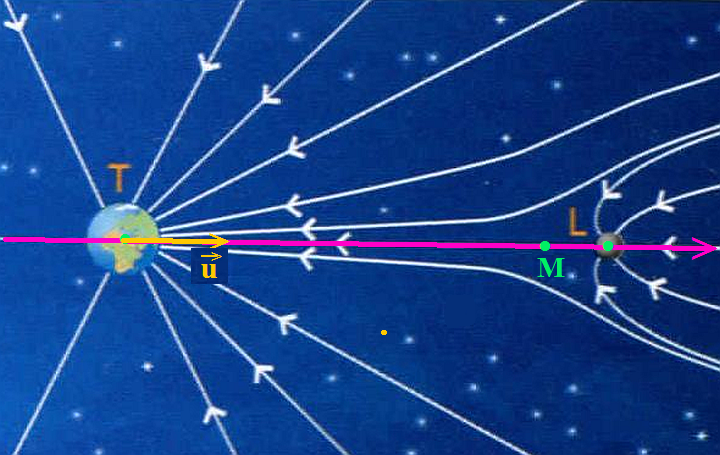
La carte de champ gravitationnel représente quelques lignes de champ créées par la terre et la Lune.

A quelles conditions, la somme (vect. champ gravit. T ) + (vect. champ gravit. L), respectivement créés par la Terre et la Lune est elle nulle?

Données:

Masse.T=5.98E24 kg
Masse.L=7.4E22 kg

Je peux répondre de façon théorique mais apparemment on attend un calcul et je ne vois pas trop lequel. Surtout que l'énoncé ne mentionne ni la distance T-L ni leurs rayons

Et comme on se situe loin de la surface terrestre je doute que 9.81N/kg puisse être utilisé ici.

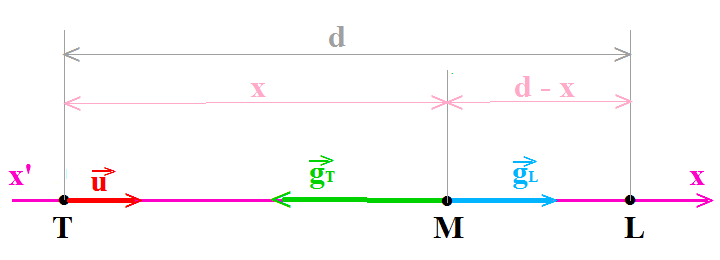
J'ai compris qu'il existe un point sur la distance entre les deux astres où les vecteurs champs s'annulent ou s'équilibrent.

Mais pour la calcul faisant intervenir les masses je ne vois pas.

(vect. champ gravit. T ) + (vect. champ gravit. L)=0 est il une bonne façon de poser le problème?

La simple lecture du cours proposé dans le livre n'est peut être pas suffisante pour que je puisse répondre...

Merci
-----

[Paraboloide_Hyperbolique]

Bonjour,

Vous pouvez utiliser la formule deux fois. Calculez l'attraction de la Terre sur un corps "test" de masse m situé à une distance du centre de celle-ci. Faites de même entre ce corps "test" et la Lune. Egalez les deux forces et faites un peu d'algèbre.

Note: le fait que vous ne connaissez pas les masses de la Terre et de la Lune n'est pas un obstacle. Notez-les simplement, par exemple, et et vogue la galère.

[Tengri]

Mais les masses sont bien données dans l'énoncé!

En revanche il n'y a aucune distance qui l'est... C'est peut être volontaire de la part des auteurs pour faire réfléchir l'élève...

La loi de gravitation universelle est bien sur dans le cours que j'ai lu mais comme elle fait appel à une distance je me demandais s'il fallait utiliser

[albanxiii]

Bonjour,

vogue la galère.

Très bien dit. Mettez vos calculs qu'on avance un peu.

[A voir en vidéo sur Futura]

[Paraboloide_Hyperbolique]

Mais les masses sont bien données dans l'énoncé!

Oui, j'ai zappé cette partie de l'énoncé. Il vaut mieux cependant travailler avec des lettres et remplacer par les données numériques à la fin, une fois la formule finale obtenue.

En revanche il n'y a aucune distance qui l'est... C'est peut être volontaire de la part des auteurs pour faire réfléchir l'élève...
La loi de gravitation universelle est bien sur dans le cours que j'ai lu mais comme elle fait appel à une distance je me demandais s'il fallait utiliser

Concernant la distance, c'est effectivement voulu par les auteurs car c'est important: il s'agit de définir un repère*. Indice: prenez pour origine le centre de la Terre.

*D'une importance souvent sous-estimée par les professeurs de lycées et mal enseignée. J'ai moi-même souffert des lacunes dans ce domaine laissées par mes anciens profs lors de mes études supérieures; et j'ai déjà vu sur ce forum plusieurs exemples de dégâts* que cela pouvait provoquer chez certaines personnes.

*Du style: la vitesse et la position sont absolues, l'accélération est nulle si l'intensité de la vitesse est constante, etc.

[Tengri]

On est vraiment obligé de choisir un objet test qui soit un tiers en plus des deux astres? J'y aurais pas pensé...

Procédons par étapes, d'abord pour la Terre:

Force exercée par T sur objet test de masse m:

Sachant que F=(G*m*(m de T)) / (Rayon de T)^2

on a : F=( (6.67E-11)m*(5.98E24) / (Rayon de T)^2 )

F=env. ( ( 4E14) m / (R de T)^2 ) N/kg

[Paraboloide_Hyperbolique]

On est vraiment obligé de choisir un objet test qui soit un tiers en plus des deux astres? J'y aurais pas pensé...

C'est un "truc" de physicien bien pratique et qui est très souvent employé. Un outil indispensable qui fait partie de la boîte à outils standard de tout bon physicien. Vous verrez qu'à la fin de vos calculs, la masse de l'objet test n'apparaîtra plus et ce sera comme s'il n'avait jamais existé.

Procédons par étapes, d'abord pour la Terre:

Force exercée par T sur objet test de masse m:

Sachant que F=(G*m*(m de T)) / (Rayon de T)^2

on a : F=( (6.67E-11)m*(5.98E24) / (Rayon de T)^2 )

F=env. ( ( 4E14) m / (R de T)^2 ) N/kg

Ok. Mais le but de l'objet test, c'est justement de la placer là ou les deux forces qui s'exerceront sur lui soient égales. C'est-à-dire à une certaine distance d qui est inconnue, et qu'il faut trouver. Dans votre formule vous supposez directement d = (Rayon de T)^2, ce qui est faux.

Procédez comme dit:

1. Calcul de la force exercée par la Terre sur l'objet test pour une distance d inconnue.
2. Calcul de la force exercée par la Lune sur l'objet test pour cette même distance (attention à l'emplacement de l'origine du repère: la distance objet test à Lune ne sera pas d, mais quelque chose qui dépend de d).
3. Égaler les deux forces et résoudre l'équation ainsi obtenue avec pour inconnue d.

Aussi, n'entrez les données numérique qu'au dernier moment, quand vous aurez une formule du type d = ...

[mach3]

Les rayons de la lune et de la terre n'interviennent pas pour répondre. Le d c'est la distance entre le centre d'un astre et le point auquel on souhaite calculer le champ créé par cet astre en ce point.
Dans le cas particulier où le point est à la surface de l'astre, d sera le rayon de l'astre, mais là il n'est absolument pas question de ça.

m@ch3

[Archi3]

en revanche la distance Terre Lune est importante, sans elle on ne peut pas calculer ce point.

[Tengri]

Voyons:

F exercée par T sur objet test (OT):

F= G*m(OT)*m(T) / (Dist. T-OT)^2

F exercée par L sur objet test (OT):

F= G*m(OT)*m(L) / (Dist. L-OT)^2

Et la somme des deux est censée faire 0

Est ce juste?

[Paraboloide_Hyperbolique]

Voyons:

F exercée par T sur objet test (OT):

F= G*m(OT)*m(T) / (Dist. T-OT)^2

F exercée par L sur objet test (OT):

F= G*m(OT)*m(L) / (Dist. L-OT)^2

Et la somme des deux est censée faire 0

Est ce juste?

On souhaites que les intensités des deux forces soient égales. Donc...

[Tengri]

C'est donc" =" et non "+" entre mes deux expressions !

[Opabinia]

Bonjour,

Le choix des signes apparaît évident dès qu'on prend la peine de tracer un schéma montrant l'orientation des vecteurs champ.

Sur l'axe joignant les centres des deux corps, orienté de la Terre vers la Lune par le vecteur unitaire

u = (1/TL).TL ,

et en tout point (M) du segment ouvert ]TL[ , les champs de gravitation produits par chacun des deux corps présentent des sens opposés etadmettent pour expressions (en posant TM = x et LM = d - x)

g_T = -G(M_T/TM²).u = -G(M_T/x²).u ;
g_L = +G(M_L/LM²).u = +G(M_L/(d - x)²).u .

Les forces de gravitation se compensent et s'annulent au point particulier vérifiant:

g_T + g_L = 0 ,

ce qui conduit à une relation simple entre (x, d) et les masses .

[Tengri]

Il me manque des bases là...

Je ne sais pas ce que c'est qu'un vecteur unitaire ni comment on le manie.

Il est vrai que une demi page de cours dans le livre c'est léger...

[Archi3]

Il me manque des bases là...

Je ne sais pas ce que c'est qu'un vecteur unitaire ni comment on le manie.

Il est vrai que une demi page de cours dans le livre c'est léger...

tu sais ce qu'est un vecteur ?

si tu sais ce que qu'est un vecteur, et ce qu'est sa norme, un vecteur unitaire est un vecteur de norme 1. Il permet d'indiquer la direction d'un vecteur quelconque indépendamment de sa norme, en écrivant A= ||A|| u où u est le vecteur unitaire dirigé parallèlement au vecteur A

sinon pour l'égalité, intuitivement, tu comprends que l'attraction de la Lune et de la Terre sont de sens opposés ? la Lune attire le point vers la Lune et la Terre vers la Terre. Ce que tu as écrit, ce sont des normes, qui sont toujours positive. Mais en réalité quand tu projettes les forces sur l'axe Terre Lune, les deux projections ont des sens opposés, et donc elles se soustraient.

Il ne faut donc pas écrire ||F_T||+||F_L||=0 mais ||F_T||-||F_L||=0 soit ||F_T||=||F_L|| Note bien que les normes étant toujours positives ou nulles, la première égalité ne serait possible que si les deux normes sont nulles, ce qui n'est évidemment pas le cas.

De façon générale, quand tu écris "la somme des forces" , il s'agit d'une somme vectorielles. Je te conseille de toujours faire un dessin en représentant les flèches des vecteurs et en les projetant sur un axe, tu visualiseras le sens des vecteurs et des projections. En choisissant (arbitrairement) une orientation vers le sens + sur l'axe, les projections sont comptées positivement quand elles sont dans le sens +, et négativement si elles sont dans le sens opposé.

C'est un peu la base du calcul avec des vecteurs, si tu ne le maîtrises pas, entraine toi car c'est important pour ne pas faire d'erreur de signe ...

[Opabinia]

(TL) représentant la norme ║TL║ du vecteur (TL), on a pour la norme du vecteur unitaire:

u = ║u║ = │1/TL│* ║TL║ = (1/TL)*(TL) = 1 .

Les vecteurs champs de gravitation, toujours attractifs, sont au niveau du point (M) colinéaires mais de sens contraires.

L'équation d'annulation du champ résultant g_T + g_L = 0 (vecteur nul)
donne après simplification:

-M_T/x² + M_L/(d - x)² = 0 ,

d'où l'expression de la distance cherchée (x) en fonction des 3 autres termes.
Si la valeur de (d) n'est pas donnée, on peut seulement calculer le rapport (x/d).

[Tengri]

Ouf il y a du travail depuis ce matin, je vais relire tout ça à tête reposée...

[Tengri]

J'ai effectivement fait un schéma pour mettre tout au clair

Mais pourquoi le vecteur u va dans le sens opposé aux lignes de champ gravitationnel terrestre?

C'est la direction qui importe pas le sens? On aurait pu le tracer depuis L tout aussi bien?

si tu sais ce que qu'est un vecteur, et ce qu'est sa norme, un vecteur unitaire est un vecteur de norme 1. Il permet d'indiquer la direction d'un vecteur quelconque indépendamment de sa norme, en écrivant A= ||A|| u où u est le vecteur unitaire dirigé parallèlement au vecteur A

Je l'ai vu en seconde je crois mais en maths seulement: le produit d'un vecteur unitaire par la norme du vecteur auquel il est colinéaire donne ce dernier vecteur?

Vaut mieux que je comprenne la chose en profondeur plutôt que la retenir telle quelle et l'appliquer de façon automatique dans un exercice de mécanique.

[Archi3]

ce que tu vois en maths est aussi utile (et peut etre probablement encore plus utilisé) en physique qu'en maths. N'hésite pas à reprendre tes cours de maths pour comprendre la physique ;

Si tu choisis un vecteur unitaire dans le même sens que le vecteur A , tu as toujours un coefficient positif entre les deux (la norme). Mais quand tu as deux vecteurs qui peuvent etre de sens opposés (ce qui est le cas ici), il va bien falloir en choisir un ! tu peux choisir un comme tu veux et écrire A= A u , où cette fois A peut etre positif ou négatif suivant que A et dans le même sens que u ou en sens opposé. A est appelée mesure algébrique, c'est donc plus ou moins la norme. Dans ce cas tu peux additionner les vecteurs (parallèles ) en additionnant les mesures algébriques et ce serait correct d'écrire F_T +F_L = 0 si tu conviens que l'une est positive et l'autre est négative (mais ça revient au même que soustraire les normes).

[Tengri]

gT = -G(MasseT/TM2).u = -G(MasseT/x2).u ;
gL = +G(MasseL/LM2).u = +G(MasseL/(d - x)2).u .

Ici l'objet test n'apparait pas? Pourquoi?

Ou alors il est confondu avec le point M d'équigravité?

[Opabinia]

Bonjour,


gT = -G(MasseT/TM2).u = -G(MasseT/x2).u ;
gL = +G(MasseL/LM2).u = +G(MasseL/(d - x)2).u

Le texte renvoyé est illisible, faute de l'emploi des indices et des exposants, ainsi que d'une notation appropriée pour les vecteurs (ici les caractères gras, convention anglo-saxonne pratique dans le cas présent):

g_T = -G(M_T/TM²).u = -G(M_T/x²).u ;
g_L = +G(M_L/LM²).u = +G(M_L/(d - x)²).u .

[Opabinia]

En l'absence de caractères gras (g_T, g_L, u) désignent des normes de vecteurs par définition positives ou nulles;

les relations correctes les concernant s'écrivent, puisque l'on a de plus u= 1 :

g_T = G(M_T/TM²) = G(M_T/x²) ;
g_L = G(M_L/LM²) = G(M_L/(d - x)²) .

Le troisième corps (de masse m négligeable) n'intervient pas, parce qu'il est ici inutile; il ne s'agit pas d'un problème de dynamique, mais de la simple recherche d'un point particulier, indépendamment du mouvement des deux astres

Ce corps placé en (M) est soumis à la résultante des forces d'attraction gravitationnelle: F = m.(g_T + g_L) ,

résultante nulle au "point d'isogravité" F = 0

ce qui implique immédiatement g_T + g_L = 0 .

[le_STI]

Salut

en revanche la distance Terre Lune est importante, sans elle on ne peut pas calculer ce point.

C'est vrai, mais ce n'est pas ce qui est demandé

A quelles conditions ....

[Tengri]

ça fait plus de 20 ans que je n'ai pas fait de physique et je suis en train de m'y remettre, donc mes mécanismes cognitifs par rapport à ça sont plutôt rouillés. J'ai eu en fin de seconde des exercices similaires à celui ci mais plus simples, avec moins d'implicites. Et où les vecteurs étaient purement indicatifs. Là il faut vraiment calculer avec et j'avais eu de réelles difficultés en seconde, en maths avec ceux ci...

Donc c'est bien ça : il n'est pas nécessaire de choisir un objet test pour calculer le champ gravitationnel des deux astres?

Pour la question du vecteur unitaire je crois que j'ai compris mais ça reste abstrait : en gros on redouble un vecteur en superposant sur ce dernier un vecteur de norme 1 de façon à être sur qu'ils ne se croisent pas (autrement dit : même direction) ?

Pour les normes il y a parfois quatre, parfois deux barres seulement?

[Tengri]

Salut



C'est vrai, mais ce n'est pas ce qui est demandé

Oui ça me pose problème ça: je suis pas sur de bien interpréter le "à quelles conditions" (au pluriel d'ailleurs...)

Formulé comme ça je n'ai pas l'impression qu'un calcul soit attendu. Pourtant tout porte à croire que si vu que l'énoncé prend la peine de fournir les masses des planètes!

[mach3]

Pour les normes il y a parfois quatre, parfois deux barres seulement?

Ce sont deux choses différentes :

|x| est la valeur absolue de x, avec x un réel
||u|| est la norme de u, avec u un vecteur

[Paraboloide_Hyperbolique]

ça fait plus de 20 ans que je n'ai pas fait de physique et je suis en train de m'y remettre, donc mes mécanismes cognitifs par rapport à ça sont plutôt rouillés. J'ai eu en fin de seconde des exercices similaires à celui ci mais plus simples, avec moins d'implicites. Et où les vecteurs étaient purement indicatifs. Là il faut vraiment calculer avec et j'avais eu de réelles difficultés en seconde, en maths avec ceux ci...

Cela vaut le coup de se les coltiner, car ceux-ci sont présents un peu partout en physique.

Donc c'est bien ça : il n'est pas nécessaire de choisir un objet test pour calculer le champ gravitationnel des deux astres?

Comme je l'ai indiqué, il s'agit d'une astuce de calcul bien pratique.

Pour la question du vecteur unitaire je crois que j'ai compris mais ça reste abstrait : en gros on redouble un vecteur en superposant sur ce dernier un vecteur de norme 1 de façon à être sur qu'ils ne se croisent pas (autrement dit : même direction) ?

Vous compliquez la vie: un vecteur unitaire est un vecteur de norme* 1. C'est tout.
N'importe que vecteur (sauf le vecteur nul) peut être normalisé en calculant:

Pour la norme considérée (ici la norme euclidienne, mais il y a en a d'autres).

[Archi3]

Comme je l'ai indiqué, il s'agit d'une astuce de calcul bien pratique.

c'est un peu plus profond qu'une "astuce de calcul" quand même. La force de gravitation s'écrit F=mg où g est l'accélération de la pesanteur. Dire que la force est nulle c'est pareil de dire que g est nul, mais cette dernière condition ne dépend pas de m. C'est donc normal qu'on ait pas besoin de m dans le calcul. Passer par les forces oblige à introduire une masse test , mais en réalité elle disparaitra du calcul ensuite par simplification.

on aurait pu s'en passer en parlant directement de champ gravitationnel et pas de force.

[Archi3]

a noter aussi que si on veut un point qui reste fixe par rapport à la Terre et la Lune, il faut tenir compte de la force centrifuge dans le référentiel en rotation avec la Lune, et ça change complètement la position du point. La condition n'est plus que la force soit nulle, mais qu'elle provoque un mouvement circulaire à la même période que la Lune, ce qui est une condition assez différente.

[Tengri]

Mais pourquoi, si l'on veut obtenir un champ gravitationnel, doit on multiplier G*(Masse/d^2) par le vecteur unitaire?

Ce dernier ayant par définition une norme de 1, ça ne fait que confirmer la valeur du champ... Mais j'imagine que c'est la seule expression mathématique rigoureuse pour le phénomène de manière à montrer qu'il se situe parfaitement dans l'axe de la droite (TL)