Bonjour,
Je cherche à résoudre numériquement une équation différentielle d'ordre 2, aux dérivés partielles...
mais je n'arrive pas à exprimer ma dérivé seconde en fonction d'un paramètre constant comme avec le pendule pesant :
https://pastebin.com/YMSGKiVM
En d'autres termes les 2 dérivés secondes m’embêtent...
Que faire ?
D'abord, il faut bien comprendre que contrairement à une équadif à une variable, le nombre de conditions limites "explose" littéralement en dimension 2+.
S'il en suffit d'une avec une équadif du 1er ordre à une variable et qu'il en faut 2 avec son pendant de 2ème ordre, avec le genre d'équation que tu évoques, il faut borner toute la "surface". C'est à dire proposer une valeur pour tous les points situés sur : Ez(xmin,t), Ez(xmax,t), Ez(x, tmin), Ez(x,tmax). Dans le cas présent, c'est donc les "bords" du rectangle qui s'étend de Ez(xmin,tmin) à Ez(xmax,tmax).
D'autre part, si tu développes les dérivées secondes, tu verras que tu peux raisonner sur base d'un point ainsi que des 4 points vicinaux. On les dénomme souvent Nord, Sud, Est et Ouest. Et c'est justement pour ça que tu as besoin de borner toute la surface des solutions.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Si c'est numérique, pourquoi ne pas utiliser la routine Python idoine ? (qui, je suis sûr, existe...)
Je fais dans le cadre de la préparation à un examen. Je n'ai donc pas le droit de me servir du manuel Python.
Aurais-tu un exemple de code à me présenter? Pour que je comprenne.
Non, désolé. De plus, je pense qu'il y a plusieurs approche (calcul itératif, etc.).Envoyé par lesurveilleur
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Bonjour,
Voir, par exemple : heat-Laplace-1D-nb.ipynb et
heat-Laplace-1D-nb.pdf
C'est l'équation de la chaleur, il n'y a donc qu'une dérivée seconde, YAPUK généraliser.
Malheureusement cela ne se généralise si aisément à partir de l'équation de la chaleur, puisqu'une dérivée seconde demande de donner aussi les vitesses.
Cette équation est une équation d'ondes dont la vitesse de propagation est variable en fonction de la distance x.
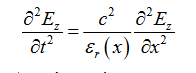
On pourrait par exemple donner comme conditions initiales les valeurs deet de sa dérivée
Mais ce n'est pas forcément ce que le prof a demandé. Dans d'autres exemples on peut vouloir fixer les extrémités en x=0 et x=L, ou encore décider qu'une extrémité est une fonction de t comme sin(t), etc etc... En fait il y a une infinité possible de problèmes et cela n'a pas vraiment de sens de vouloir "résoudre l'équation" si on ne décrit pas les conditions aux limites.
Pour le problème avec les conditions initiales, ce qu'on fait souvent est de discrétiser l'axe des x et l'axe des t. La valeurs de la solution en t+delta(t) sont calculées à partir des valeurs voisines en t. Pour cela on doit écrire la dérivée seconde au moyen des différences centrales. On trouve de nombreux textes qui décrivent cette méthode sur le web (chercher "résolution numérique équation des ondes" dans un moteur de recherche).
Salut,
Je connais ça dont la simplicité tue :
https://python-prepa.github.io/edp_chaleur.html
Aller à 4.2
Biname
Dernière modification par Biname ; 29/09/2022 à 23h38.
