Theoreme de Shannon

[stefjm]

En fait tout le débat est là. pas d'observation directe (le décalage n'est pas une observation directe car il transforme le signal sous test, le sampling et FFT non plus puisqu'on bascule dans les maths avec des possibilités infinies). Mais on s'est compris et je suis d'accord que ce serait bizarre, défiant le bon sens.

Mais qu'est-ce qu'une observation directe?

Très simplement on peut écrire
cos t= cos(-t) = 1/2 (cos(t)+cos(-t))

Dans les trois cas, on décrit le même signal.

Si on parle d'un signal analogique réel (ex électrique), et non complexe (en "bande de base" comme on dit dans le jargon des DSP-guys que je côtoie au boulot), je ne vois pas comment.

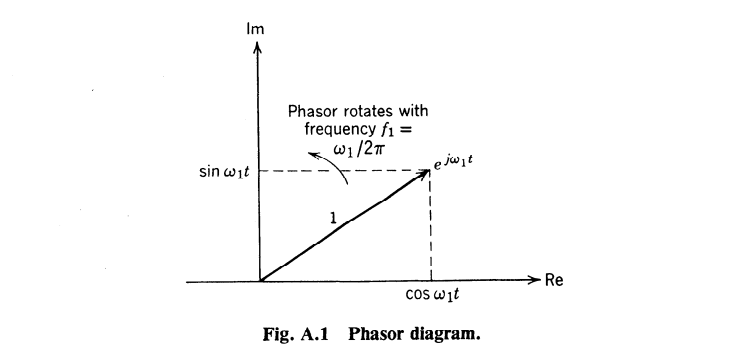
Si je suis ma rigueur mathématique, je ne sais pas faire un sinus avec une seule raie. Il m'en faut deux, symétriques par rapport à zéro.

S'il n'y a qu'une seule raie, cela correspond à e^(it), un signal complexe, dont la partie réelle est le cos et la partie imaginaire est le sin.

Obtenir un sinus en analogique se fait facilement avec une double intégration (1/p^2) et un rebouclage (BO/(1+BO) qui donnera la réponse impulsionnelle 1/(p^2+1)=1/[(p-i)(p+i)] correspondant au sinus t.

Et du coup, c'est moi qui ne saurait pas faire un circuit physique de réponse impulsionnelle complexe 1/(p-i) correspondant à e^(it) !
-----

[Gwinver]

Bonsoir.

Le schéma de modulateur BLU de Wikipedia ne fait pas intervenir les fréquences négatives, le filtre utilisé est un filtre à quartz et non pas un filtre passe bas.
Une autre méthode pour obtenir de la BLU est le mélangeur équilibré à réjection de fréquence image qui ne passe pas non plus par les fréquences négatives. Les réjections de porteuse et de fréquence image sont simplement obtenue par annulation grâce à des sommations de signaux en opposition de phase.

[stefjm]

Une autre vision du problème, voici un extrait d'un textbook parmi tant d'autres:



Source: https://onlinelibrary.wiley.com/doi/...471221090.app1

-> l'analyse d'un signal du monde physique ("actual signal") ne voit que la projection sur l'axe horizontal, il n'a pas accès au sens de la rotation du "phasor".
J'espère que ça ne contredit pas ce que j'ai dit plus haut

Pour le coup là, on est servi en fréquences négatives!
On profite clairement des bonnes propriétés de l'exponentielle complexe et des propriétés des transformées de Fourier (Laplace, Melin, etc...).
C'est très cool de remplacer les convolutions par de simple produit et vice-versa.

[stefjm]

Bonsoir.

Le schéma de modulateur BLU de Wikipedia ne fait pas intervenir les fréquences négatives, le filtre utilisé est un filtre à quartz et non pas un filtre passe bas.
Une autre méthode pour obtenir de la BLU est le mélangeur équilibré à réjection de fréquence image qui ne passe pas non plus par les fréquences négatives. Les réjections de porteuse et de fréquence image sont simplement obtenue par annulation grâce à des sommations de signaux en opposition de phase.

Oui, et cela enlève la moitié du spectre, spectre décalé dans le positif par la modulation.
Et s'il faut enlever cette moitié de spectre, c'est bien qu'il "existe" et n'est pas un truc pas physique qu'on obtient à cause de la modulation.

[GBo]

Bon, vous m'avez convaincu.

[stefjm]

J'aime bien ce graphe en 3D qui montre les projections d'une hélice sur 3 plans :
t,x : cos t
t,y : sin t
x,y : e^(it), cercle

[GBo]

Bon, vous m'avez convaincu.

Attendez une minute... à regarder de plus près (j'ai étudié tout ça à l'école mais tout oublié !), les équations modélisant la modulation d'amplitude par un mixer idéal montrent bien que c'est la manip de modulation qui créé les 2 sidebands à partir du message m(t):
https://en.wikipedia.org/wiki/Amplit...ation#Analysis

[GBo]

Le modulation AM hardware revient à faire cette multiplication, ce n'est pas anodin:

Ensuite pour arriver à y(t), utiliser les identités de la trigo.

[Gwinver]

Bonsoir.

Oui, et cela enlève la moitié du spectre, spectre décalé dans le positif par la modulation.
Et s'il faut enlever cette moitié de spectre, c'est bien qu'il "existe" et n'est pas un truc pas physique qu'on obtient à cause de la modulation.

Là, j'ai du mal à suivre.
Aucun problème avec le spectre de l'AM, il est symétrique autour de la porteuse, c'est directement de la physique.
Mais toujours pas de mise en évidence de fréquences négatives.

[GBo]

Je dirais plutôt : c'est de l'électronique !
Si on considère que la modulation = juste une translation des fréquences présentes dans le signal m(t), il serait logique de penser que m(t) avait un spectre miroir négatif avant la translation.
Sauf que la modulation (également utilisée pour l'upconversion, c'est idem) est réalisée par un composant s'appelant un mixer qui n'est autre qu'un multiplieur, et c'est lui qui engendre les sidebands comme le démontre la trigo.

What happens when signals are mixed
It is found that if two signals are passed through a non-linear circuit, then additional signals on new frequencies are formed. These appear at frequencies equal to the sum and difference frequencies of the original signals du lien donné plus haut.

In other words if signals at frequencies of f1 and f2 enter the mixer, then additional signals at frequencies of (f1+f2) and (f1-f2) will also be seen at the output.

https://www.electronics-notes.com/ar...ing-basics.php

[stefjm]

Bonjour,
Je suis d'accord avec tout ce qui a été dit et tout cela abonde pour des fréquences négatives dans le spectre d'un sinus.

Un spectre de modulation AM (par mélangeur, multiplieur, etc...) est symétrique par rapport à la fréquence centrale (via le produit de deux sinusoides, si on veut rester simple et ne pas parler de convolution coté fréquence. Cela revient au même, ce sont des maths.)

On a donc pour une modulation la somme (fc+fm) et la différence (fc-fm).
Si on module à fc=0, le même calcul donne 0+fm et 0-fm.

Comment expliquer dans ce cas que vous ne voulez pas de -fm dans le spectre du sinus normal non modulé ?

Et dans le cas des repliements de spectre, cela peut être la partie négative (image, artéfacte, symétrique...) qui vient foutre le souk dans le cas d'un sous-échantillonnage.

Ce qu'il y a de cool avec les maths, c'est qu'on arrive facilement à se mettre d'accord.

Cordialement

[stefjm]

Je dirais plutôt : c'est de l'électronique !
Si on considère que la modulation = juste une translation des fréquences présentes dans le signal m(t), il serait logique de penser que m(t) avait un spectre miroir négatif avant la translation.
Sauf que la modulation (également utilisée pour l'upconversion, c'est idem) est réalisée par un composant s'appelant un mixer qui n'est autre qu'un multiplieur, et c'est lui qui engendre les sidebands comme le démontre la trigo.

Pourquoi sauf que?

C'est aussi des maths.
Un produit (multiplication) coté temporel, donne un produit de convolution coté fréquentiel (et vice-versa).
Et un produit de convolution effectue le fameux décalage en fréquence.

D'où le raccourci : un mélangeur décale le spectre.

Qu'on considère les spectres fréquentiels ou les signaux temporels, la conclusion est heureusement la même.

http://users.polytech.unice.fr/~lero...#modulationcos
http://users.polytech.unice.fr/~lero...al/node19.html

[GBo]

(...)
Un spectre de modulation AM (par mélangeur, multiplieur, etc...) est symétrique par rapport à la fréquence centrale (via le produit de deux sinusoides, si on veut rester simple et ne pas parler de convolution coté fréquence. Cela revient au même, ce sont des maths.)

On a donc pour une modulation la somme (fc+fm) et la différence (fc-fm).
Si on module à fc=0, le même calcul donne 0+fm et 0-fm.
[...]

Un LO à 0 Hertz connait pas ! On est dans le forum physique

[Gwinver]

Bonjour.

Bon, avec un oscillateur local à Fo, et un signal à Fs. Le mélange produit donc : Fo, Fo+Fs et Fo-Fs.
Pour obtenir une fréquence négative, il faut Fs > Fo.

Après mélange, il serait donc possible de placer un filtre passe bas à fréquence de coupure très inférieure à Fo, voire même proche du continu, éliminant ainsi Fo et Fo+Fs.
En cas d'existence d'un signal à fréquence négative, il y aurait de la puissance RF en sortie de ce filtre.

En fait, ce n'est pas ce qui se passe, lorsque la fréquence de Fo est inférieure à Fs, la fréquence intermédiaire est : Fs-Fo, c'est la réception infradyne.
Voir le chapitre 11 de ce cours : https://www.leradioscope.fr/2016-05-...ue/chapitre-11

[stefjm]

Un LO à 0 Hertz connait pas ! On est dans le forum physique

0.01Hz et le raisonnement reste le même et conduit à la même conclusion, tant d'un point de vu maths que d'un point de vue technologique.

Bon, avec un oscillateur local à Fo, et un signal à Fs. Le mélange produit donc : Fo, Fo+Fs et Fo-Fs.
Pour obtenir une fréquence négative, il faut Fs > Fo.

Après mélange, il serait donc possible de placer un filtre passe bas à fréquence de coupure très inférieure à Fo, voire même proche du continu, éliminant ainsi Fo et Fo+Fs.
En cas d'existence d'un signal à fréquence négative, il y aurait de la puissance RF en sortie de ce filtre.

Il y en a et c'est d'ailleurs exactement ce que tu dis par la suite.
en -F0+Fs

En fait, ce n'est pas ce qui se passe, lorsque la fréquence de Fo est inférieure à Fs, la fréquence intermédiaire est : Fs-Fo, c'est la réception infradyne.
Voir le chapitre 11 de ce cours : https://www.leradioscope.fr/2016-05-...ue/chapitre-11

Réception qui s'explique très bien avec les fréquences négatives, justement.

Je laisse tomber la porteuse à F0, inutile pour le point qui nous occupe.

Signal de spectre -Fs ,+Fs
La modulation déplace ce spectre de +F0 et de -F0.
Cas infradyne F0 est plus petit que Fs

On obtient alors 4 raies : 2 négatives et 2 positives
-F0-Fs , F0-Fs "0" -F0+Fs , F0+Fs

Un passe bas de fréquence de coupure inférieur à F0 laisse passer -F0+Fs (positive) et F0-Fs (négative).

C'est quand même assez fou qu'en étant d'accord avec les mêmes calculs et la même technologie, on arrive à des conclusions différentes.

Pour moi, les fréquences négatives et positives sont de même type physique. Aussi physique l'une que l'autre ou aussi non physique l'une que l'autre.
Je ne vois absolument pas pourquoi il faudrait privilégier l'une par rapport à l'autre?

Pour aller dans vos sens, je peux comprendre qu'on replie le spectre négatif sur le positif pour cacher le négatif puisque symétrique, donc inutile.
Perso, je trouve les spectres que positifs moins compréhensibles que les spectres symétriques.
Cela rompt les symétrie sympa liées aux transformées de Fourier.
Un signal réel (math) à un spectre symétrique.

Après c'est une affaire de gout personnel, mais pas de critère physique ou non physique derrière.